Terminal滑模控制仿真实验
2018-10-11赵海滨陆志国于清文颜世玉
赵海滨, 刘 冲, 陆志国, 于清文, 颜世玉
(东北大学 机械工程与自动化学院, 辽宁 沈阳 110819)
滑模变结构控制方法设计简单、鲁棒性强,能够克服参数不确定和外部干扰的影响[1-2]。在普通的滑模控制中,通常都是选择一个线性的滑模面,使得系统轨迹在达到滑动模态后的运动是渐进稳定的,不能在有限时间内收敛到零。为了获得更好的控制性能,一些学者提出了Terminal滑模(Terminal sliding mode,TSM)控制策略[3]。
TSM具有有限时间收敛的优点,而且对模型误差和外部干扰具有较好的鲁棒性[4-6]。但是在系统接近平衡状态时,TSM存在奇异问题。文献[7]提出了非奇异Terminal滑模(NTSM)控制方法;文献[8-9]提出一种非奇异快速Terminal滑模控制方法并应用于跟车控制;文献[10]提出基于指数趋近律的非奇异Terminal滑模控制方法。针对系统接近平衡状态时TSM控制收敛速度比较慢的问题,文献[11]提出了快速Terminal滑模(FTSM)控制方法;针对FTSM存在奇异问题,文献[12]提出了非奇异快速Terminal滑模(NFTSM)控制方法。
倒立摆的摆角控制是典型的二阶不确定非线性系统。本文以该系统为研究对象,分别采用TSM、NTSM、FTSM和NFTSM进行摆角的平衡控制,采用Matlab/Simulink软件建立了系统的仿真模型,并对仿真的结果进行了分析和讨论。该仿真实验不仅有助于学生对Terminal滑模控制理论的理解,而且让学生理解滑模控制的实际应用。通过仿真过程,能够培养学生的编程能力和工程意识,激发学生的学习兴趣和创新精神。
1 二阶非线性不确定系统
二阶不确定非线性系统表示为
(1)
其中f(x1,x2)和g(x1,x2)为已知连续非线性函数,且g(x1,x2)≠0,u为控制输入;d(t)为外部干扰,且d(t)≤μ,μ>0。
以单级倒立摆的摆角控制问题[3]为研究对象,动力学方程为
(2)
其中g为重力加速度,x1和x2分别为摆角和摆速。m为摆杆的质量,mc为小车质量,且M=m+mc。l为摆长的一半,u为控制输入。外部干扰d(t)=0.5 sint。
2 Terminal滑模控制
2.1 传统TSM控制器
传统TSM控制器的切换函数为
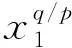
(3)
其中:β>0,p和q为正奇数,且p>q。
采用指数趋近律

ε·sgn(s)
(4)
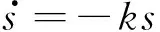
传统TSM控制器设计为
(5)
在式(5)中,由于q/p-1<0,在x1=0,x2≠0时会有奇异问题。
2.2 非奇异Terminal滑模控制
为了克服传统TSM存在的奇异问题,可以采用非奇异Terminal滑模控制(NTSM)。NTSM的切换函数为
(6)
参数β>0,p和q为正奇数(p>q,且1
(7)
2.3 快速Terminal滑模控制
为了克服传统TSM在接近平衡状态时收敛速度比较慢的缺点,提出了快速Terminal滑模控制(FTSM)。FTSM的切换函数为
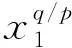
(8)
参数α>0,β>0,p和q为正奇数,且p>q。采用指数趋近律,FTSM控制器设计为
(9)
FTSM比TSM具有更快的收敛速度。由于在控制器中存在q/p-1<0,FTSM仍然存在奇异问题。
2.4 非奇异快速Terminal滑模控制
NFTSM具有FTSM的优点,又克服了奇异问题。NFTSM的切换函数为
s=x1+α·sgn(x1)|x1|r1+β·sgn(x2)|x2|r2
(10)

(11)
NFTSM的收敛速度比TSM快,但是比FTSM慢。由于NFTSM避免了奇异问题,因此具有很好的工程应用。
3 Matlab仿真实验
在倒立摆动力学方程中,小车质量mc=1 kg,摆杆的质量m=0.1 kg,l=0.5 m,重力加速度g=9.8 m/s2。倒立摆的初始状态为x1=0.1,x2=0。
在所有的控制器中,取k=10,μ=2,ε=0.01。在TSM和NTSM控制器中取β=1,p=5,q=3。在FTSM控制器中取α=1,β=1,p=5,q=3。在NFTSM控制器中取α=10,β=1,r1=5/3,r2=7/5。
为了削弱抖振,在各控制器中采用饱和函数sat(s)代替符号函数sgn(s),饱和函数的表达式为

(12)
其中:δ>0,δ称为边界层。边界层通常取非常小的数,本文取δ=0.001。
Matlab/Simulink软件功能强大、使用简单方便,并且对问题的描述和求解符合人的思维习惯和数学表达习惯,已经广泛应用于动态系统仿真[13-15]。由于倒立摆的动力学方程和控制器都比较复杂,不适合采用普通Simulink模块来建立仿真模型,因而采用M-函数和积分模块等来建立仿真模型。M-函数为Simulink中用户自定义功能模块库中的Matlab Function模块。在仿真过程中,采用变步长的ode45算法,最大步长为0.0001 s,仿真时间为5 s。采用NFTSM控制器时,利用Matlab/Simulink软件建立的仿真系统如图1所示。积分模块Integrator的初始值设置为0,Integrator1的初始值设置为0.1。仿真结果可以通过Scope模块直接显示,同时通过ToWorkspace输出到工作空间中。
根据式(2)建立倒立摆的系统模型,并添加干扰信号。在图1中,倒立摆模块内的程序如下:
functionddx=fcn(dx,x,u,t)
mc=1;m=0.1;a=0.5;g=9.8;
dt=0.5*sin(t);
S=a*(4/3-m*cos(x)*cos(x)/(mc+m));
fx=g*sin(x)-m*a*dx*dx*cos(x)*sin(x)/(mc+m);
fx=fx/S;
gx=cos(x)/(mc+m);
gx=gx/S;
ddx=fx+gx*u+dt;
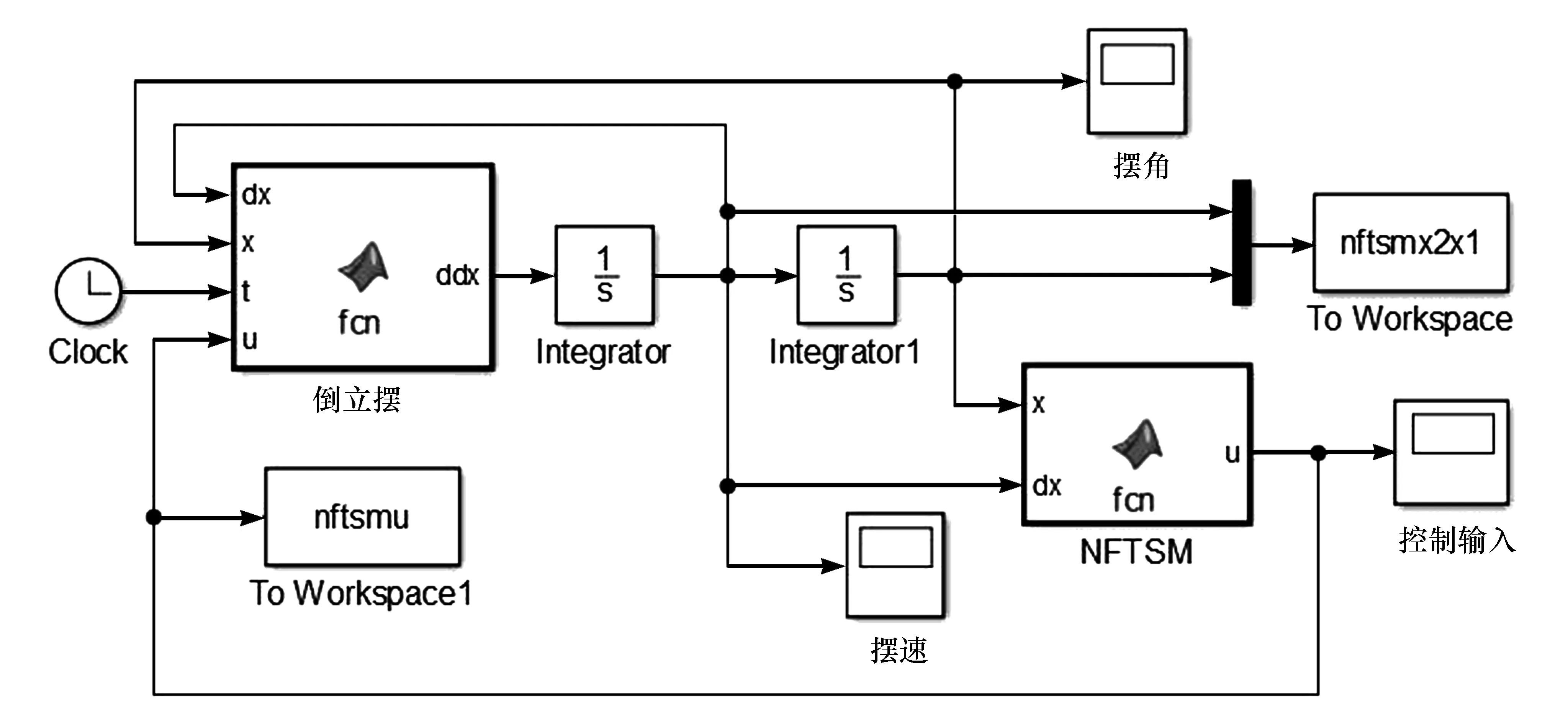
图1 NFTSM仿真实验系统
在图1中,采用NFTSM进行倒立摆的控制。NFTSM控制器采用式(11)进行编程,并且采用饱和函数代替符号函数。NFTSM模块内的程序如下:
functionu=fcn(x,dx)
mc=1;m=0.1;a=0.5;g=9.8;
S=a*(4/3-m*cos(x)*cos(x)/(mc+m));
fx=g*sin(x)-m*a*dx*dx*cos(x)*sin(x)/(mc+m);
fx=fx/S;
gx=cos(x)/(mc+m);
gx=gx/S;
alpha=10;beta=1;r1=5/3;r2=7/5;
s1=alpha*sign(x)*abs(x)^r1;
s2=beta*sign(dx)*abs(dx)^r2;
s=x+s1+s2;
delta=0.001;
d=abs(s/delta);
if d<=1
sat=s/delta;
else
sat=sign(s/delta);
end
k=10;mu=2;epsilon=0.01;
m1=sign(dx)*abs(dx)^(2-r2);
m2=(1+alpha*r1*abs(x)^(r1-1));
m=m1*m2/(beta*r2);
u=-(fx+k*s+(mu+epsilon)*sat+m)/gx;
在各个控制器作用下的摆角如图2所示。摆角从初始位置0.1迅速变为0,TSM的趋近速度比NTSM略快;FTSM的趋近速度最快;NFTSM刚开始时趋近速度和FTSM一样快,在接近0点时,速度下降;NFTSM比FTSM的趋近速度慢,是因为起始位置为0.1,已经非常小。如果起始的位置比较大,NFTSM的优势才能显现出来。

图2 控制器作用下的摆角
在各个控制器作用下的摆速如图3所示。对于摆速的绝对值,NFTSM方法具有最大值,为0.315,NTSM具有最小值,为0.231。FTSM方法摆速趋近的速度最快,NFTSM方法摆速趋近的速度最慢。

图3 控制器作用下的摆速
在各个控制器作用下,控制输入u如图4所示。在3.14~3.19 s区间,TSM和FTSM会出现奇异问题。在3.1~3.25 s之间进行局部放大,如图5所示。NTSM和NFTSM能够有效地避免奇异现象,控制输入比较平滑,也没有出现抖振现象。
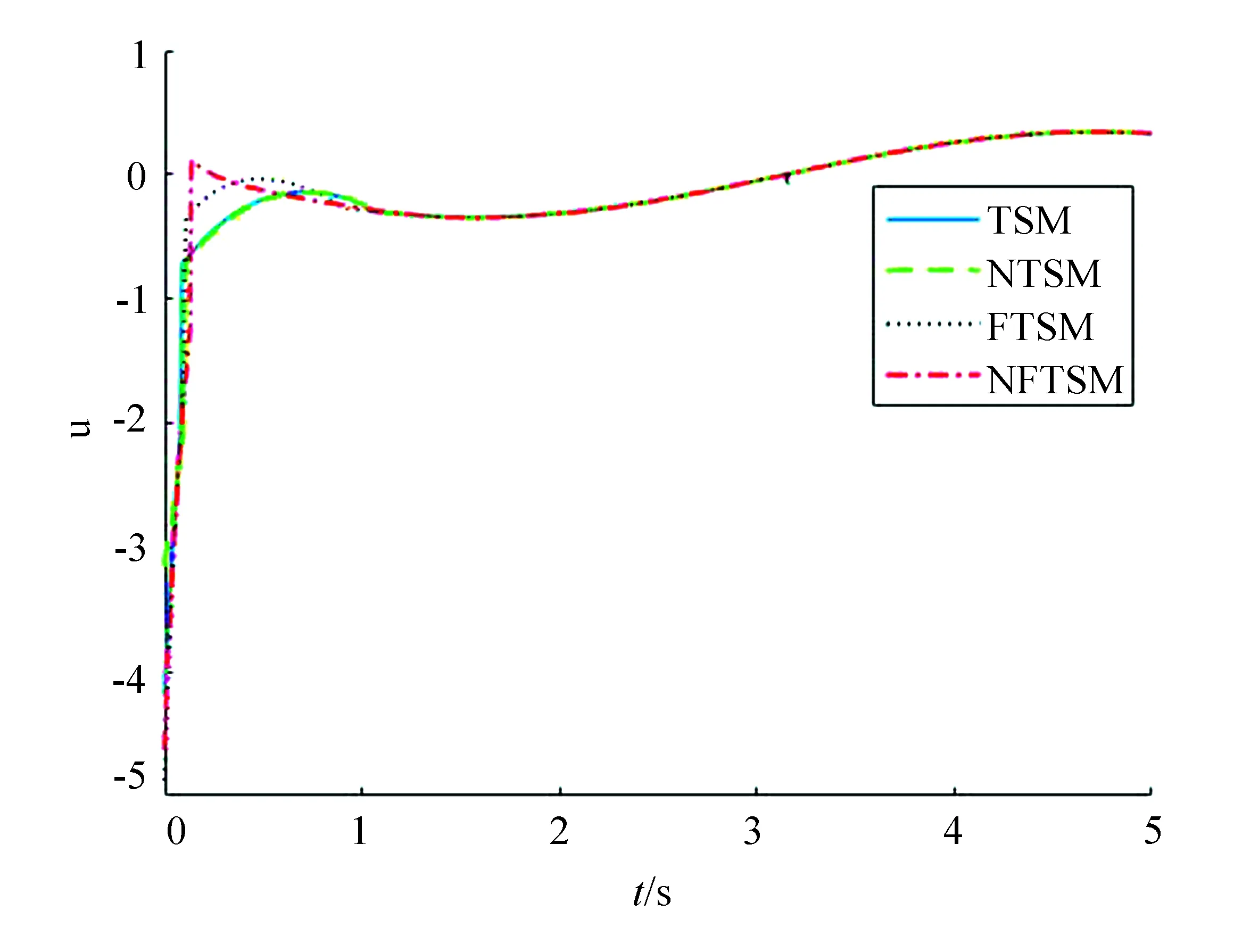
图4 控制器作用下的控制输入
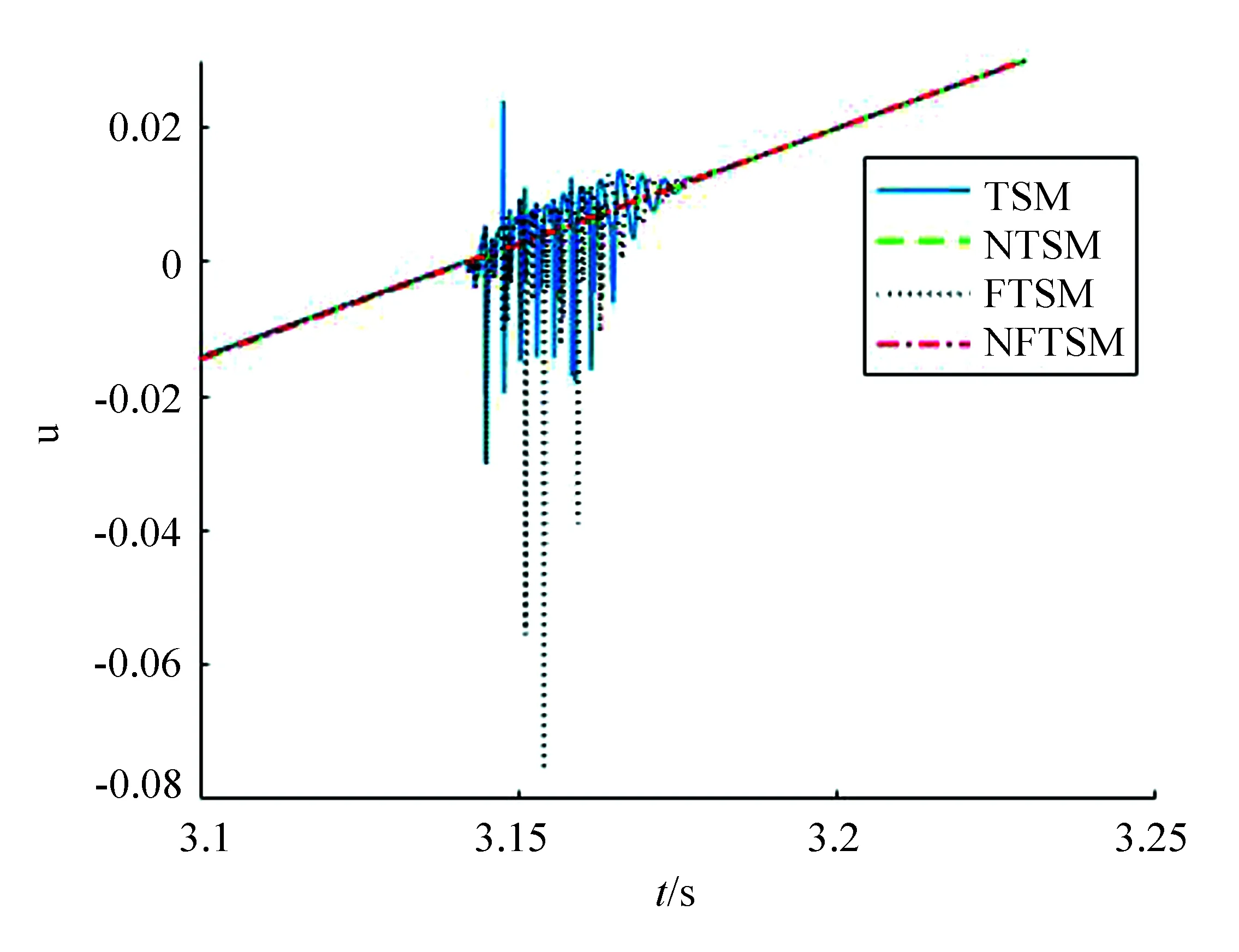
图5 控制输入的局部放大
4 结语
本实验以倒立摆的摆角控制问题为研究对象,分别采用TSM、NTSM、FTSM和NFTSM进行摆角的平衡控制。采用Matlab/Simulink软件进行了仿真实验,并对实验结果进行了分析和讨论。该仿真实验不仅有助于学生对Terminal滑模控制理论的理解,而且有助于学生学习滑模控制的实际应用。此外,学生可以通过Matlab/Simulink软件进行仿真实验,对其他滑模控制方法进行验证,观测不同实验结果,从而激发学习兴趣,培养编程能力和科研创新能力。
