东风岗1号杨材积生长曲线方程的建立与应用

赵玉恒

(黑龙江省森林与环境科学研究院,黑龙江 齐齐哈尔 161005)

树木的生长因树种和品种的不同，均有其自身的生长规律，相同树种也会因品种不同而差异显著。为研究相同树种不同品种间存在的这种差异，筛选了大树平均木进行树干解析，利用SPSS曲线参数估计法模块，分别以树高、直径和林龄为自变量自动拟合11种材积曲线模型[1]，选择最适模型建立大树材积生长曲线方程，为生产应用提供科学参考。

1 树干解析及材积生长量拟合

在富锦市东风岗林场30 a生试验林内，我们选择东风岗1号杨平均木进行树干解析，其树高、胸径和材积分别为27.54 m、27.60 cm和0.651 16 m3。根据树干解析数据，我们利用SPSS曲线估计程序中的线性、对数、反向、二次、三次、复合、幂、S、增长、指数和Logistic等11个参数估计法，分别以树高、直径和龄阶为自变量对已观测的树木材积进行拟合，见表1。

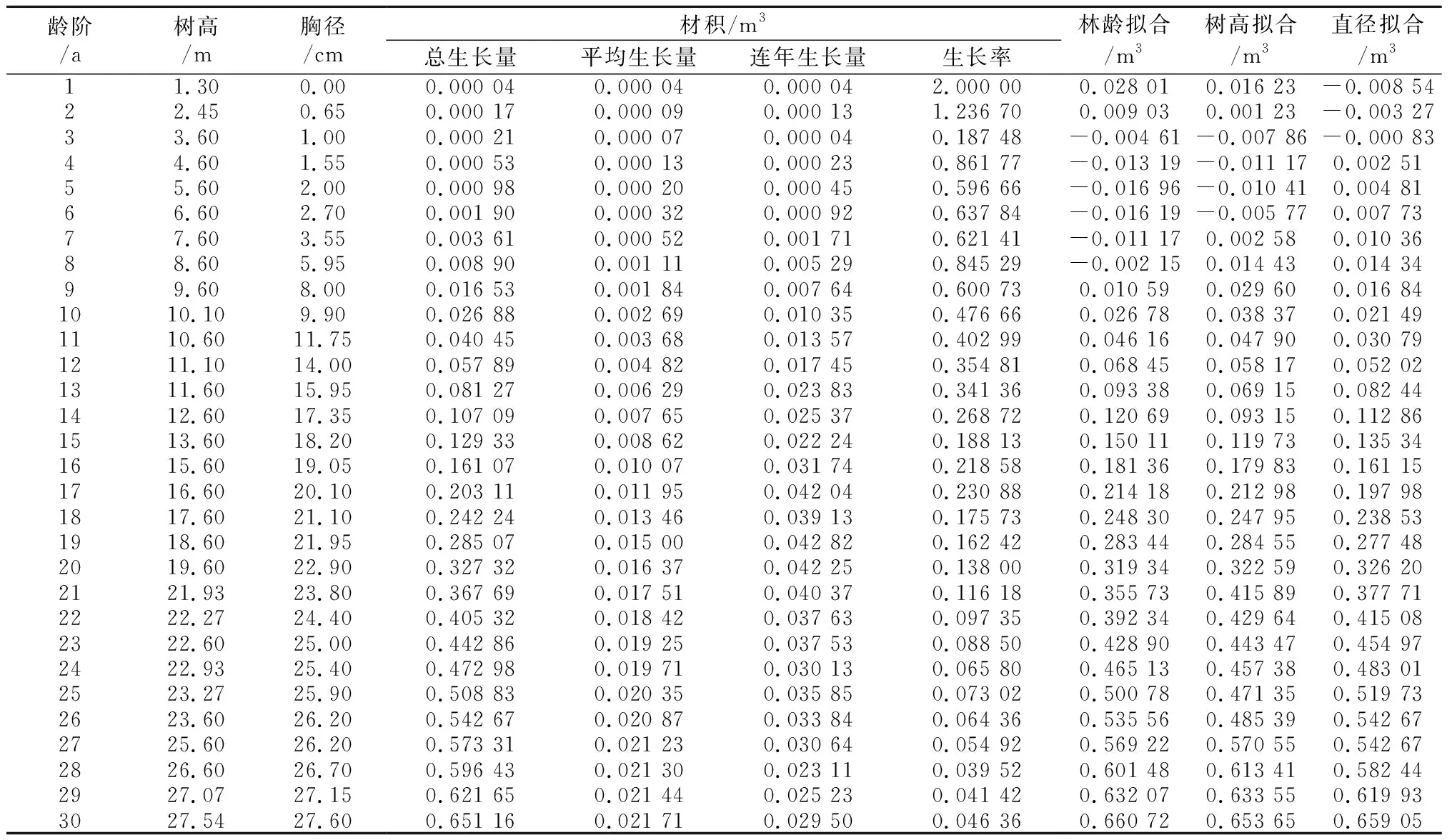
表1 东风岗1号杨解析木生长进程调查汇总表

2 大树材积生长曲线方程建立

我们分别以树高、直径和林龄为自变量，利用SPSS曲线估计程序对材积生长曲线进行拟合，其中Cubic(立方)曲线与实测结果曲线拟合效果最好。

2.1 以树高为自变量对立木材积进行拟合

以树高为自变量，对立木材积进行拟合，拟合结果见图1-图2。

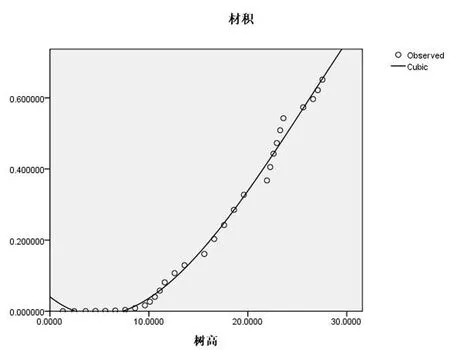
图1 以树高为自变量获得的12种曲线拟合图

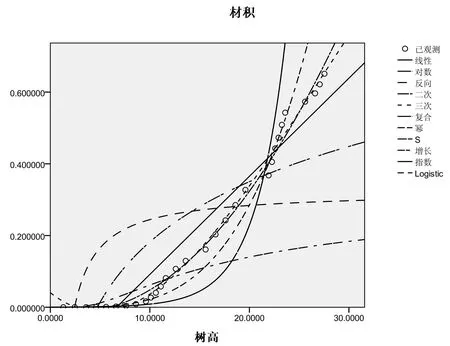
图2以树高为自变量获得的拟合度最高的材积生长曲线图

最佳生长曲线的确定决定系数R2为0.993，标准误差为0.020，F值为1 296.07，P值为0.000。获得以树高为自变量的材积生长模型表达式：

Y=0.041-0.022x+0.002x2-3.133×10-5x3

式中:Y表示材积，X表示树高。

2.2 以直径为自变量对立木材积进行拟合

以直径为自变量，对立木材积进行拟合，拟合结果见图3-图4。

最佳生长曲线的确定决定系数R2为0.999，标准误差为0.009，F值为5 810.44，P值为0.000。获得以直径为自变量的材积生长模型表达式：

Y=-0.009+0.009x-0.001x2+6.47×10-5x3

式中，Y表示材积，X表示直径。

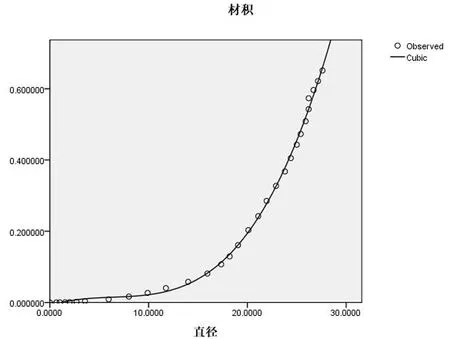
图3 以直径为自变量获得的12种曲线拟合图

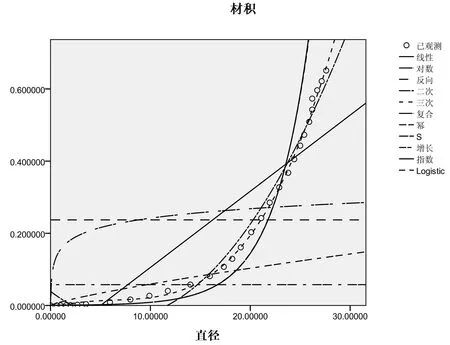
图4 以直径为自变量获得的拟合度最高的材积生长曲线图

2.3 以林龄为自变量对立木材积进行拟合

拟合结果见图5-图6。

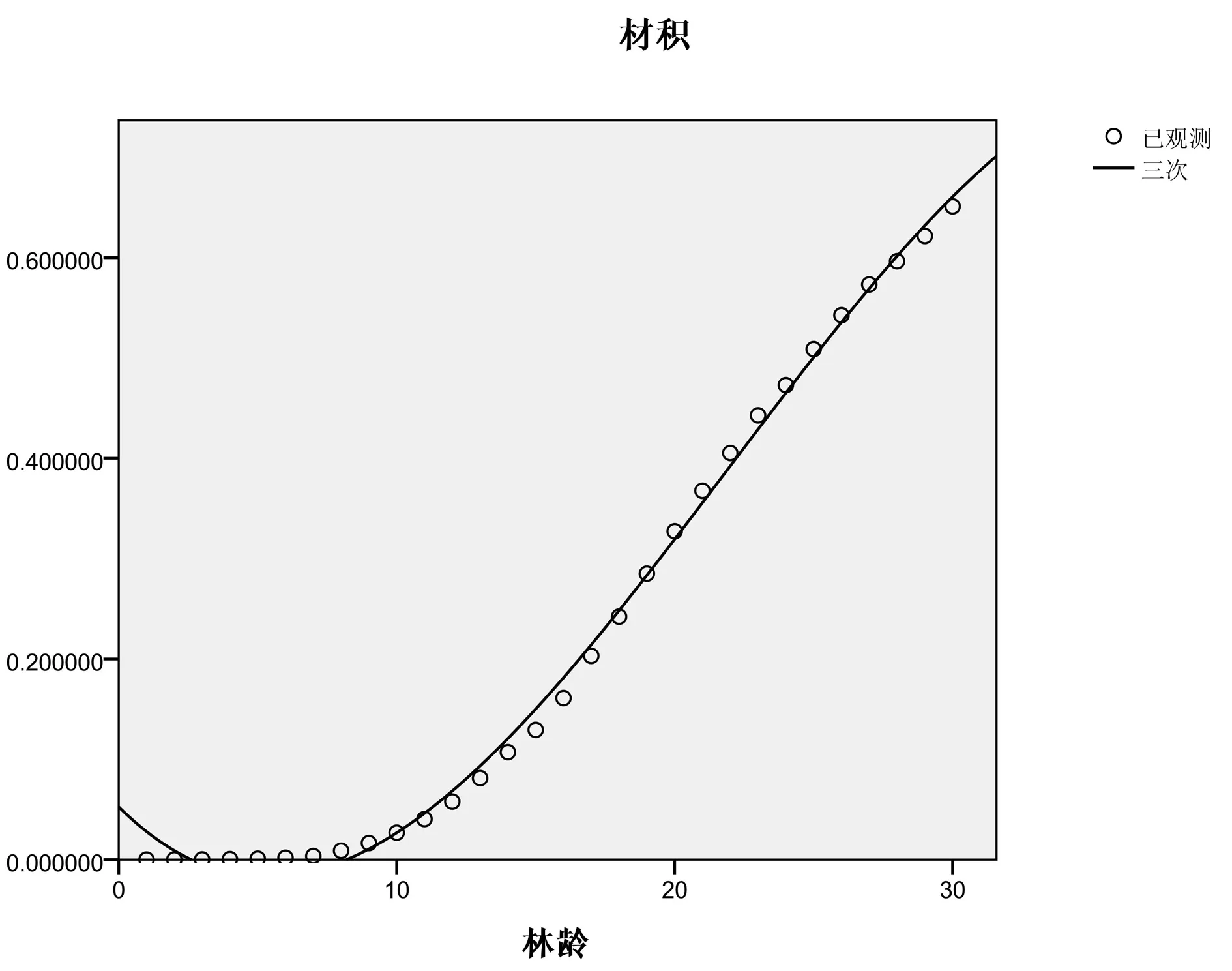
图5 以龄阶为自变量获得的12种曲线拟合图

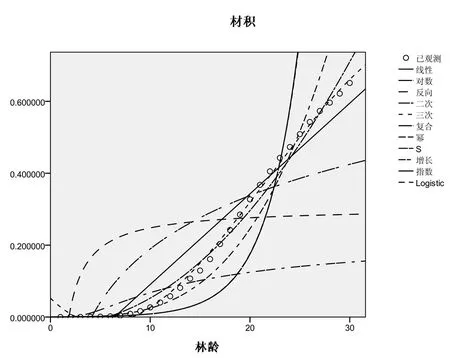
图6 以龄阶为自变量获得的拟合度最高的材积生长曲线图

最佳生长曲线的确定决定系数R2为0.997，标准误差为0.013，F值为2 924.73，P值为0.000。获得以林龄为自变量的材积生长模型表达式：

Y=0.053-0.027x+0.003x2-4.493×10﹣5x3

式中，Y表示材积，X表示林龄。

根据 Cubic(立方)曲线拟合结果，我们建立了东风岗1号杨材积拟合曲线生长模型(表11)，结果表明，在α=0.001时，三个方程均有统计学意义，其中，以直径拟合的曲线方程决定系数和F值均最大，标准误最小，以林龄拟合的次之，以树高拟合的误差相对较大。

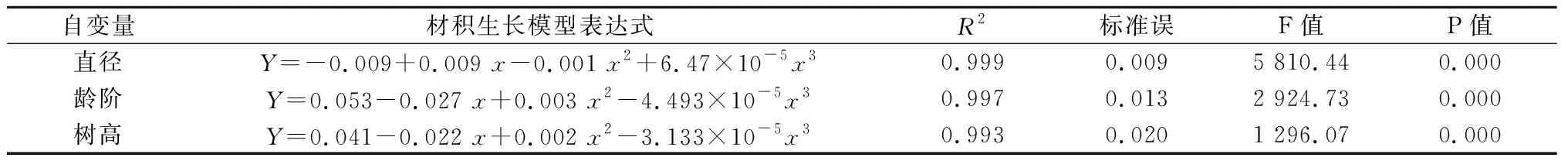
表11 树高、直径和龄阶与材积的拟合曲线模型

为验证三个方程的实用性，我们将树干解析数据中的树高、直径和林龄分别代入相应方程，计算结果表明，林龄在10 a前拟合的材积生长量数值与实测数值误差较大，10年生后的数值与实测值误差较小，可以应用。在生产中根据要求的精度选择应用一种方程进行材积估算与预测，为林业生产提供科学参考。

3 小结

不同树木的树高和胸径生长都有一定的规律，因树种和品种而不同，我们以树高、直径和林龄为自变量，对其材积生长曲线进行拟合，选择最佳方案进行材积生长量预测，为立木材积计算提供了重要参考。