具有埋深校正的岩石静态脆性指数计算方法——以吉木萨尔凹陷二叠系芦草沟组为例

李国欣，毛 锐，王振林，牟立伟

（1.中国石油 勘探与生产分公司，北京 100011；2.中国石油 新疆油田分公司 勘探开发研究院，新疆 克拉玛依 834000）

准噶尔盆地吉木萨尔凹陷二叠系芦草沟组致密油资源丰富，但储集层的渗透率极低，一般无自然产能，需要形成一套适用性强的岩石脆性测井计算方法以指导水力压裂，进而获得经济产量。

岩石的脆性是储集层压裂改造设计中必须要考虑的重要参数，当脆性较好时，岩石容易产生剪切破裂形成人造裂缝与节理，由此改善储集层的渗流能力。国内外学者对岩石脆性评价做了大量的研究，总体上可以概括为岩石力学实验法[1-5]、弹性参数法[6-8]和矿物法[9-10]。文献［1］—文献［4］基于岩石力学实验，利用应力—应变曲线、岩石强度、岩石硬度等参数表征岩石脆性；文献［5］利用单轴压缩应力与拉伸应力的比值计算了不同岩石的脆性；文献［6］利用纵横波速度计算的杨氏模量和泊松比评价岩石脆性；文献［7］和文献［8］基于钻井时岩石诱导缝对纵横波速度的频散特性，利用纵横波速度计算了岩石的脆性和可压裂性；文献［9］和文献［10］利用脆性矿物含量占总矿物含量的比例评价岩石的脆性。然而，上述岩石脆性评价方法都有一定的局限性：①岩石力学实验法虽然是最为直接的岩石脆性评价方法，但需要大量的取心和岩心的破坏性实验，实验成本高，无法实现沿井轴的连续性脆性表征；②弹性参数法虽然在行业内应用广泛，但能够准确表征岩石脆性的是静态弹性参数，动态弹性参数不能直接表征岩石脆性，动、静态弹性参数之间的转换关系没有统一的模型，需要根据研究区特点建立；③矿物法需要先明确脆性矿物类型，适用于黏土矿物分布形式稳定、围压变化小的地层，而研究区的实际地层情况并不满足上述条件。在前人研究的基础上，结合研究区目的层岩石力学实验结果，提出了一种具有埋深校正的基于孔隙度和黏土矿物含量的岩石脆性测井计算方法，实现了研究区岩石脆性的精确表征，为储集层压裂改造提供了测井技术支撑。

1 动、静态脆性指数模型的建立

研究岩石脆性的岩石力学参数一般分为静态弹性参数和动态弹性参数。利用岩石力学实验数据计算得到的是静态弹性参数，而利用地球物理测井资料计算得到的是动态弹性参数。静态弹性参数可以作为岩心数据标定动态弹性参数，从而形成纵向上连续的脆性测井表征模型。

为了建立适用性强的岩石静态脆性表征模型，结合研究区动、静态弹性参数和孔隙度实验数据（表1），笔者优化选择了静态杨氏模量和静态泊松比建立模型[11]：

表1 研究区储集层岩石弹性参数、孔隙度及黏土矿物含量

利用杨氏模量和泊松比建立岩石脆性的原因：①杨氏模量和泊松比是描述岩石在不同应力下应变程度的常用参数，可以由岩石力学实验准确获得；②杨氏模量与泊松比在数值上差很多倍，通常杨氏模量的取值范围为1.1～100.0 GPa，泊松比为0～0.5，二者的比值可以很好地区分不同岩石的脆性；③由（1）式可知，在轴向应力恒定的情况下，轴向应变量越小，杨氏模量越大，同时，大量实验数据分析可知，大部分岩石产生的横向应变量一般小于轴向应变量，由（2）式可知，横向应变量越小，岩石的泊松比就越小。综上所述，杨氏模量和泊松比的比值能很好地表征岩石脆性。

同理，也可以用动态杨氏模量和动态泊松比建立岩石动态脆性表征模型：

2 动、静态脆性指数转换模型

动、静态弹性参数之间存在明显差异（表1），这是由于地层是各向异性的，矿物、孔隙、流体等与岩石结构相关的因素使得岩石的动、静态脆性指数存在差异[12-16]，所以动、静态脆性指数之间需要进行转换。溶蚀孔是研究区发育的主要孔隙类型[17]，这种孔隙相互不连通，使得声波时差测井对其不敏感，从而造成声波时差测井计算的动态弹性参数与岩石力学实验测量的静态弹性参数存在差异。同时，黏土矿物的存在也使得动、静态弹性参数之间差异进一步增大。因此，建立动、静态弹性参数转换模型时需要考虑孔隙度和黏土矿物含量。

理论认为孔隙度和黏土矿物含量的增加都会导致岩石脆性降低[18]。从动、静态弹性参数与孔隙度和黏土矿物含量的关系（图1）可以看出，动态弹性参数受孔隙度影响较大，而静态弹性参数受黏土矿物含量影响较大。因此，动、静态脆性指数转换模型可以表述为

利用表1的黏土矿物含量、孔隙度、杨氏模量和泊松比数据进行拟合，建立了在实验室最大围压35 MPa下的动、静态脆性指数模型，即：

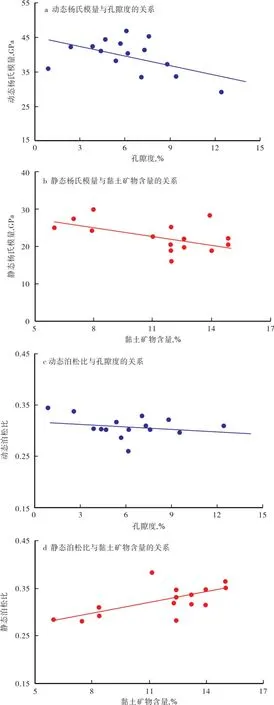
图1 研究区动、静态弹性参数与孔隙度和黏土矿物含量的关系

利用（9）式计算的脆性指数与实验测量结果吻合度较高（表2），说明基于岩石孔隙度和黏土矿物含量的转换模型精度较高，具有适用性。

3 埋深校正

地层埋藏越深，围压越大，岩石的脆性就越差，复杂缝网就越难形成。若要准确获得地层条件下的岩石脆性，需要对脆性指数进行埋深校正。从吉木萨尔凹陷二叠系芦草沟组一块不同围压条件下岩石的动、静态弹性参数变化趋势（图2）可以看出，随着围压的增加，静态弹性参数逐渐增大，而动态弹性参数基本没有变化。产生这种现象的原因是声波速度对围压的变化不敏感，导致声波速度计算的动态弹性参数变化不明显。因此，脆性指数的埋深校正需要选取与声波速度无关的参数。

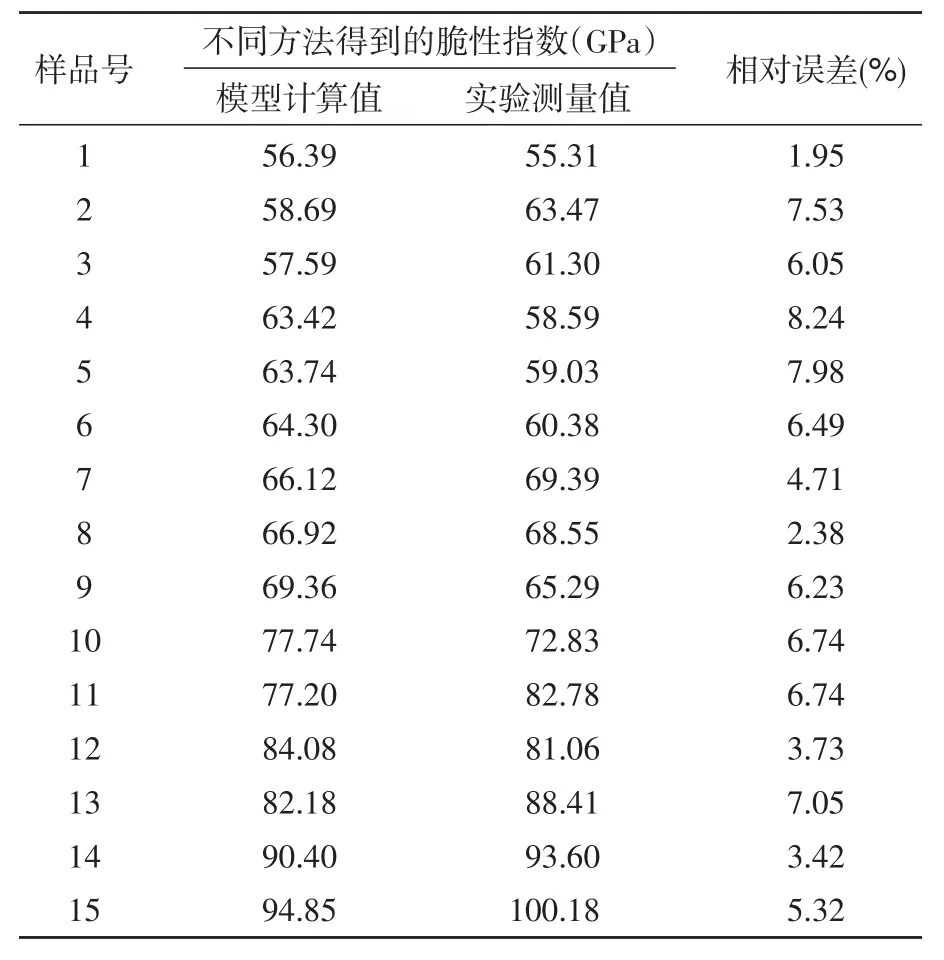
表2 脆性指数模型计算结果与实验测量结果对比

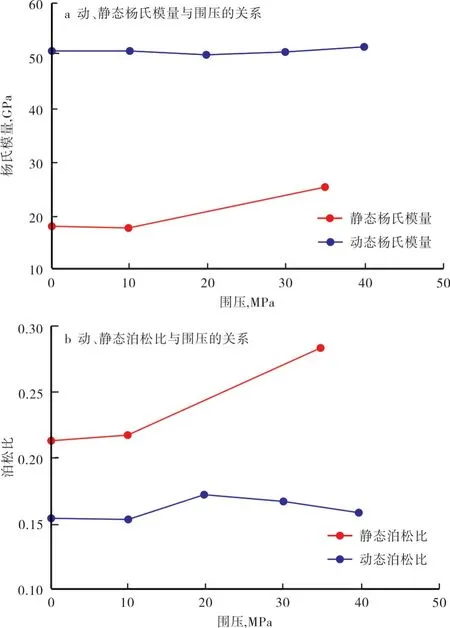
图2 动、静态弹性参数与围压的关系

选择3组有代表性的岩心，测量在不同围压条件下的静态脆性指数（表3）。从表3可以看出，围压越大，岩石脆性指数越小，即围压与静态脆性指数呈负相关关系。为了突出围压变化对岩石脆性的影响，定义围压增大因子是最大围压35 MPa与某一围压的差值；同时，定义岩石脆性增大系数是某一围压下静态脆性指数与最大围压35 MPa下的静态脆性指数之比。则岩石脆性增大系数与围压增大因子可表示为

表3 不同围压下静态脆性指数

由脆性增大系数与围压的相关性分析可知（图3），两者之间呈现较好的指数关系，则（10）式可以表示为

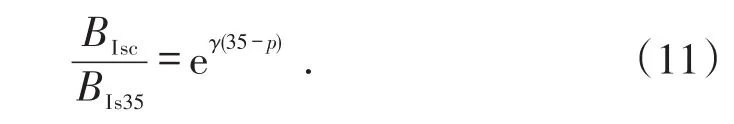
图3 不同围压下脆性增大系数的变化

然而，图3中每个指数拟合关系式的幂都不一样，分析认为是由黏土矿物含量的不同导致的，因此压力校正指数应与黏土矿物含量具有函数关系，其拟合关系式为

将（9）式、（12）—（15）式代入（10）式，得到经过埋深校正的静态脆性指数：

由于泊松比和杨氏模量的数值存在数量级的差异，需要对（16）式做归一化处理：

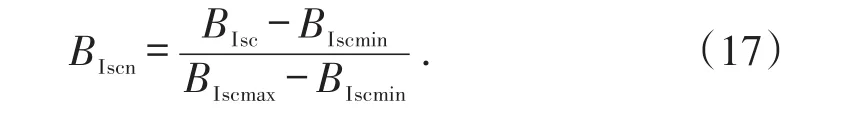
4 应用效果

用本文方法计算研究区吉174井的脆性指数（图4），可以看出，计算的脆性指数与岩心分析的脆性指数吻合良好。图5是研究区4口井芦草沟组本文方法计算的脆性指数和Rickman方法计算的脆性指数对比，可以看出，本文方法计算的脆性指数随着深度的增大而减小，符合岩石脆性随埋深增大而减小的一般规律，而国外Rickman方法计算的脆性指数则随着深度的增大而增大，说明本文的方法更具有适用性。同时，本文方法已经在研究区大规模推广使用，脆性的纵向连续表征为“甜点体”平面展布研究提供了技术支撑。

图4 研究区吉174井的计算脆性指数和岩心分析脆性指数对比

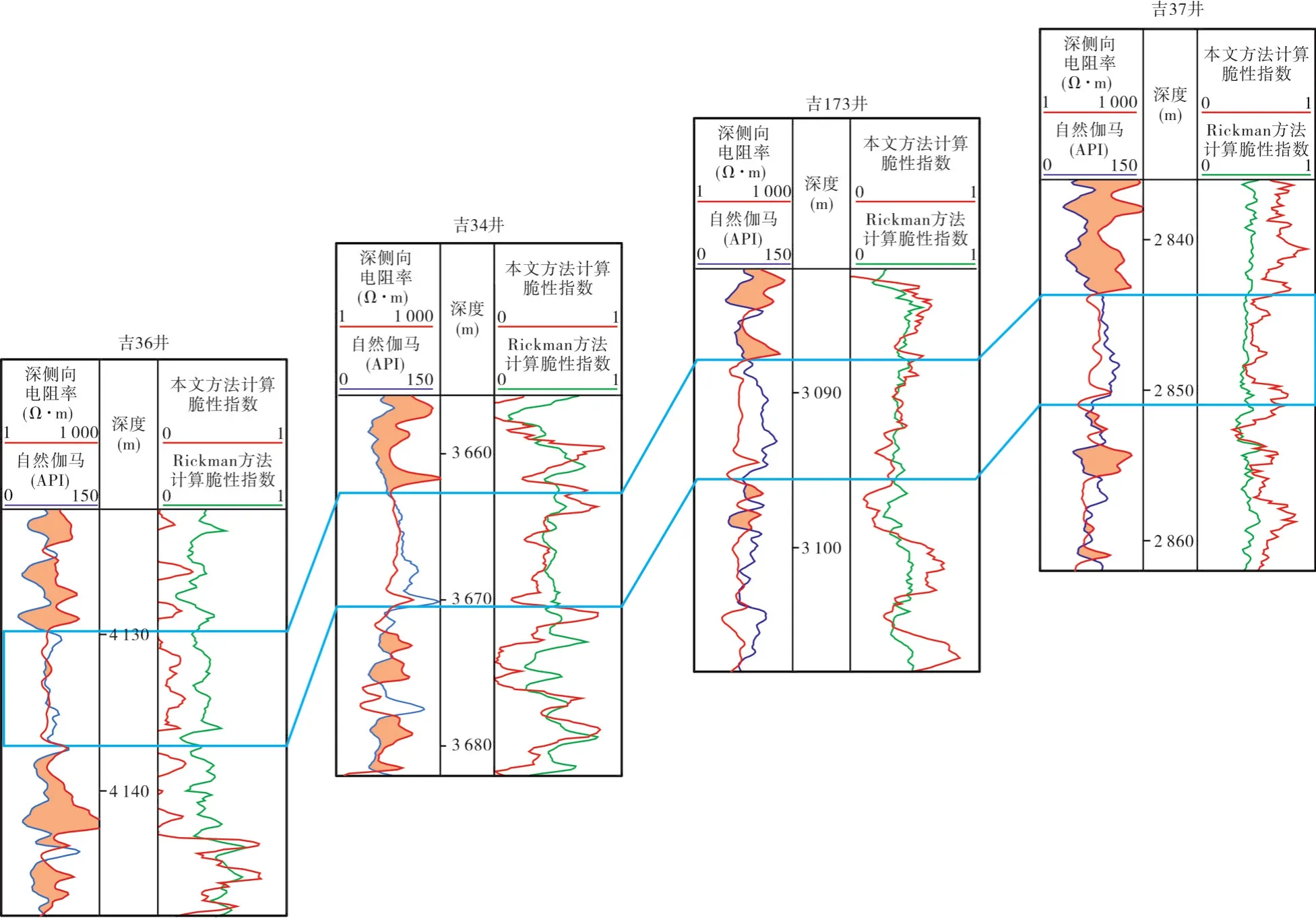
图5 研究区4口井芦草沟组脆性指数计算结果对比

5 结论

（1）研究区岩石动态弹性参数受孔隙度影响较大，而静态弹性参数受黏土矿物含量影响较大，建立动、静态脆性指数转换模型时需要考虑主要影响因素。

（2）声波速度对围压的变化不敏感，不能利用声波速度对静态脆性指数进行校正。本文基于脆性增大系数，利用黏土矿物含量对静态脆性指数进行了校正。

（3）与国外成熟的储集层脆性评价方法相比较，本文方法更符合储集层脆性特征，计算结果与岩心分析脆性指数较吻合。

符号注释

BId——动态脆性指数，GPa；

BIs——静态脆性指数，GPa；

BIs35——围压35 MPa下的静态脆性指数，GPa；

BIsc——某一围压下的静态脆性指数，GPa；

BIscmax——处理井段最大静态脆性指数，GPa；

BIscmin——处理井段最小静态脆性指数，GPa；

BIscn——归一化后的静态脆性指数，无量纲；

cp——地层压力系数，无量纲；

Ed——动态杨氏模量，GPa；

Es——静态杨氏模量，GPa；

f1——以孔隙度为自变量的校正函数；

f2——以黏土矿物含量为自变量的校正函数；

g——重力加速度，m/s2；

h——垂深，m；

p——某一深度点的围压，MPa；

p0——上覆地层压力，MPa；

pf——流体压力，MPa；

Vcl——黏土矿物含量，无量纲；

vp——纵波速度，m/s；

vs——横波速度，m/s；

Z——脆性增大系数；

ϕ——孔隙度，无量纲；

νd——动态泊松比，无量纲；

νs——静态泊松比，无量纲；

ρ——岩石密度，kg/m3；

ρb——密度测井值，kg/m3；

ρw——地层水密度，kg/m3；

γ——压力校正指数，无量纲；

Δσ——轴向应力变化量，GPa；

Δε1——轴向应变量，无量纲；

Δε2——横向应变量，无量纲。