低仰角条件下短脉冲微波传播问题分析

汪海波，李 平，方文饶，张 帅

（西北核技术研究所，西安710024；高功率微波技术重点实验室，西安710024）

在低仰角条件下，天线传输电磁波会产生遮挡、多径干扰和衰落等问题。在雷达低仰角工作及地空数据链路等工程应用上，前人已对电磁波的低仰角传播问题作了较为深入的研究［1－5］。根据特定的工程需求，研究的关注点会有不同，如地空数据通信问题研究中会关注低仰角地空信道的大尺度衰落、多径到达和多普勒扩展等现象［1－3］，雷达应用中也关注低仰角特性，特别是米波雷达，更关注低仰角状态下的测角能力及多径干扰抑制等问题［4－5］。

在本文关注的实际工程问题中，地面辐射源为高频段几十纳秒微波短脉冲，经过低仰角单程传播，空中平台接收信号，因此重点关注是否产生额外的功率衰落。因为不同工程应用的关注点有所不同，所以对本文问题进行分析，不能直接套用其他场景的下电磁波传播问题分析结论。本文从波动说的基本概念出发，分析电磁波传播中可能出现的遮挡、多径到达和天线波束分裂等问题，并进行了案例估算，提出了工程上的应对措施。

1 短脉冲微波传播问题分析

低频电磁波的波长更长，传播时容易产生绕射、衍射现象；高频电磁波更接近于光学传播规律，传播时容易产生遮挡现象。高频电磁波传播中产生的遮挡现象不能简单地使用几何光学理论进行评估，而应利用波动理论，即 Huygens原理进行评估。Stratton－Chu公式［6］是Huygens原理在电磁学上的表现形式。

除波长外，信号带宽也是影响电磁波传播的重要因素之一。若受到多径因素的影响，窄带信号会出现接收信号幅度涨落的现象，如发生小尺度衰落；宽带信号则会有多径到达、包络畸变等现象。低仰角条件下，应关注短脉冲微波的多径到达和包络畸变现象，同时也需要考虑地面对天线辐射的影响所造成的波束分裂现象。如果电磁波发射、接收或中间的散射存在相对运动，则电磁波传播信号就会产生多普勒扩展。但对于短脉冲微波信号，可以忽略传播过程中的多普勒效应。

2 模型介绍

2.1 透波屏模型

对于电磁波遮挡问题，文献［7］给出了一个经典的透波屏模型，如图1所示。在发射源和接收点中间放置一个吸收屏，中心在连线上，法线平行于连线，如图1（a）所示。中心完全透波（透射因数τ＝1），τ向外按平方指数关系衰减，如图1（b）所示。定义透波孔有效半径ρ0是τ衰减到原来的e－1处的半径值，则

采用透射因数渐变规律是为了避免透波孔尺寸与波长之间的谐振。

图1 透波屏模型［7］Fig.1Penetrating wave screen model［7］

通过Stratton－Chu积分，接收天线处的电场强度为

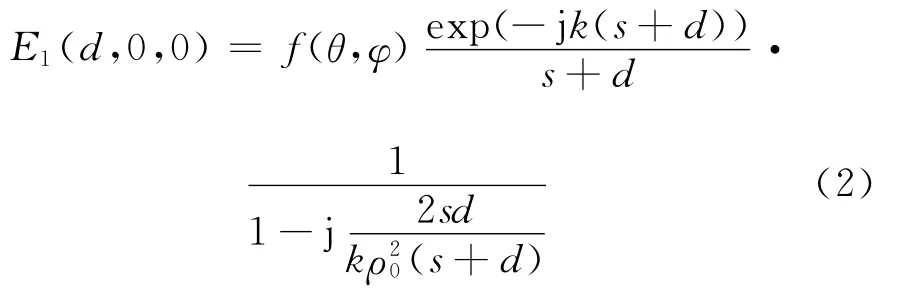
其中，f（θ，φ）为天线远场距离归一化值；s和d分别为发射源到达屏和接收端到达屏的距离；k为电波传播波数。在式（2）中取ρ0∞，则

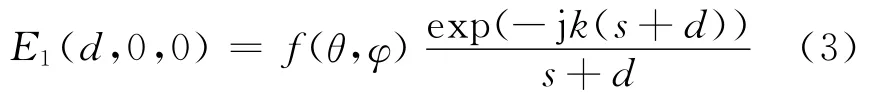
其中，E1（d，0，0）表示无任何遮挡的情况下接收天线处电场强度。结合式（2）和式（3），得到遮挡引起的电场强度衰落为

其中，

在ε2足够小的情况下，

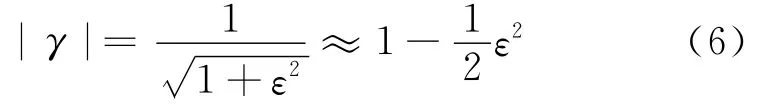
可以得到

从式（5）和式（6）可知，当发射、接收位置及频率确定时，透波孔有效半径ρ0越小，则｜γ｜越大，即在传播过程中电磁波的电场强度衰落越多。因此，障碍物越靠近连线，其产生的遮挡作用越大。

2.2 Fresnel半径

Fresnel椭球［7］是工程上理解波动现象、粗略进行遮挡和多径到达判断的近似工具。它是一个围绕着发射源和接收端连线的旋转椭球体，以发射源和接收端两点作为椭球的两个焦点，如图2所示。第n个Fresnel椭球表示的边界为

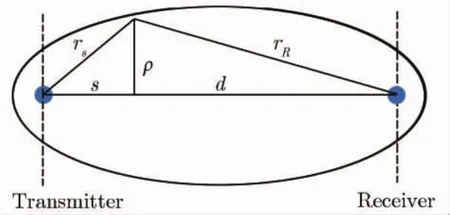
图2 Fresnel椭球Fig.2Ellipsoid of Fresnel zone

采用Taylor近似得到第n个Fresnel半径为

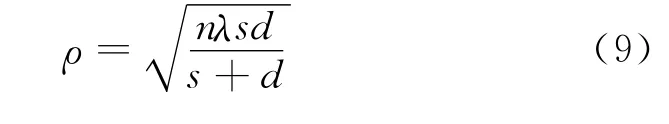
工程上将第1个Fresnel半径（简称Fresnel半径）作为粗略评估是否发生遮挡现象的依据。

2.3 两路径模型

两路径模型［8］，如图3所示。考虑了电磁波直达波和地面一次散射波，发射源和接收端距离地面高度分别为h1和h2，两个站点间的距离R远大于天线高度。因此，直达波和一次散射波的传播路径分别为

图3 两路径模型Fig.3Model of two－path propagation

使用Taylor近似得到

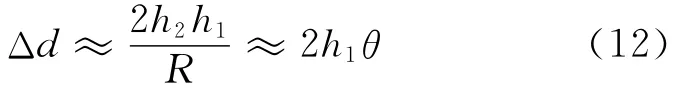
其中，θ为仰角。假设直达波和一次反射波的幅度相同，并且反射面产生了半波损失，那么接收端电场强度的表达式为

其中，λ为波长；P为发射功率；G为发射天线增益。sin（·）表示在不同仰角条件下接受信号幅度产生的“幅度调制”。

若式（13）中sin（·）＝1，则电场强度随距离的衰减关系与自由空间传播是一致的。在h1和h2固定的情况下，接收信号的幅度随距离R会有涨落现象，即波束分裂现象。波束分裂的物理含义，如图4所示。

图4 波束分裂现象Fig.4Antenna beam lobe spliting

3 案例估算分析

3.1 对电磁波遮挡现象的评估

根据2.1中透波屏模型计算得到的Fresnel半径，可作为是否发生遮挡现象的工程判据。地面发射端和空中平台接收端的Fresnel半径ρ1为

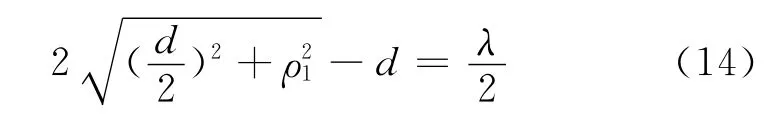
若地面发射端和空中平台间距离为100km，载波为10GHz，则计算得到 Fresnel半径ρ1为27.4m。在该椭球内出现的地物，如建筑、山峰等，都会对电磁波传播产生遮挡。

3.2 多径到达现象的评估

在分析多径到达现象时，也可使用Fresnel半径进行描述。对于短脉冲微波，如果多径因素在时域上刚好能被区分，则判断多径到达影响的Fresnel半径ρ1为

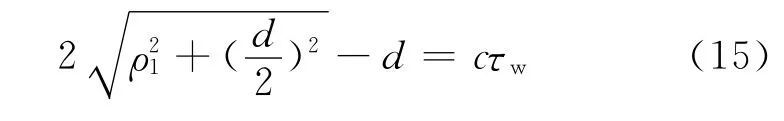
其中，c为光速；τw为微波信号的脉冲宽度。对于脉宽为30ns的短脉冲微波，使用Taylor展开近似方法计算ρ1，则

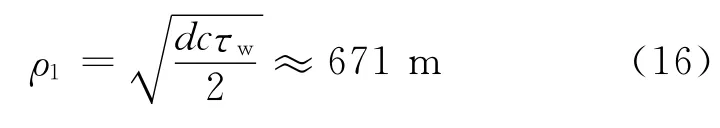
在该椭球内出现的强散射，会产生强多径到达信号。该信号与主脉冲相互叠加，会产生包络畸变现象，畸变的地方可能产生增强，也可能产生减弱。

图5为多径到达产生包络畸变的示意图，主达波和次达波相差13.23ns，产生了包络形状的畸变。图6为多径到达不产生包络畸变的示意图，主达波和次达波相差40.23ns，不产生包络形状的畸变。

图5 多径到达产生包络畸变Fig.5Influence by multipath arrival

图6 多径到达不产生包络畸变Fig.6Non－influence by multipath arrival

3.3 天线波束分裂现象评估

在本文所关注的实际工程问题中，脉冲宽度决定了一次反射波与主到达波在时域上不能分离。因此，天线波束分裂问题表现为主到达信号受到一次反射波传播的干涉影响。

以载波频率为10GHz，脉冲宽度为30ns，地面发射天线相位中心离地为6m，空中平台相对地面高度为2km，空中平台与地面发射天线间的距离为50～100km进行分析。图7给出了仰角和波程差随距离的变化关系。可见，仰角从1.9°下降到0.3°，波程差减小，波程差最大值约为13个波长，远小于30ns对应的300个波长。

图7 仰角、波程差随距离的变化关系Fig.7Elevation and wave－path difference vs.distance

图8 为按照两路径模型计算的归一化电场强度随距离的变化关系。可见，一次地面反射波对主达波产生干涉，在不同距离上会出现电场强度的涨落。这表明，如果天线主瓣靠近地面而产生波束分裂，则导致在不同距离处的空中平台接收到的电磁波幅度发生涨落。

图8 归一化电场强度随距离的变化Fig.8Normalized electric field strength vs.distance

4 应对措施

为避免遮挡现象，应该保证相应Fresnel半径对应的椭球内不存在任何遮挡，否则会使电磁波传播产生未知的衰落。实际工程应用中，在任务规划时，需要查看地形图及建筑分布图等，必要时通过三维数字地图判断电磁波传播的遮挡情况。

为避免多径现象，要求相应Fresnel半径对应的椭球内没有强散射，但由于相应Fresnel半径较大，所以实际中往往难以控制。但是，多径现象产生干扰的条件是强多径到达信号，而在X波段，地面散射作用多表现为漫反射，产生强的前向散射概率较小。实际工程应用中，在任务规划时，应尽量回避水域及其他可能产生强的前向散射的因素，即可保证工程需求。

地面天线波束分裂的原因类似于多径现象，用两路径模型可进行定性描述。由于地面天线波束分裂产生的衰减位置是未知的，实际工程应用中，要求地面天线主瓣不打地，以回避主瓣分裂的风险。