基于ARMA模型的盾构隧道结构损伤识别*

方怀霞 罗 辉 付 文

(1.湖北水利水电职业技术学院建筑工程系 武汉 430070; 2.华中科技大学土木工程与力学学院 武汉 430074)

城市轨道交通的健康服役对于城市的正常运行至关重要。如果城市轨道交通的某段路线出现故障，将危及到整个地铁网络线路，对市民出行造成严重困扰，还会造成恶劣的社会影响。为解决这一问题，近年来，越来越多的专家学者对盾构隧道的损伤识别进行研究。诸如小波分析法和自回归移动平均(ARMA)模型法[1-3]等在结构健康监测方面应用较广。本文采用基于自回归移动平均(ARMA)模型的结构动态分析，对盾构隧道进行损伤定位研究。首先介绍时间序列模型应用于结构损伤识别的原理；然后采用数值模型算例和缩尺模型实验验证该方法在盾构隧道结构损伤定位中的适用性和正确性。

1 基于时间序列模型的损伤识别方法

1.1 应用ARMA方法进行系统识别

在外界激励下竖直方向上的地下隧道结构的运动方程为

(1)

x=u-vg

(2)

式中：vg为在全球方向上的地面位移的矢量。将式(2)代入式(1)，可改写为

(3)

由方程(3)的解可得出，通过应用逆z变换找到线性ARMA模型的系数如下。

x(k)+a1x(k-1)+ … +anx(k-2n)=

b1F(k-1)+b2F(k-2)+ … +bnF(k-2n)

(4)

式中：x(k)为由驱动负载产生F(t)的输出；a1，a2，…,an为自回归(AR)系数；b1，b2，…,bn为滑动平均(MA)系数。

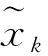
(5)

E(wjwj)=σ2δij

(6)

将方程(5)代入方程(4)，有

由此可见，参数的估计将由于噪声的干扰而偏移，其由ξ(k)表示。为了减少后续分析中的误差，引入测量的加速度信号的自相关函数作为构建ARMA模型输入的替代。

文献[4]表明，动态结构响应的自相关函数保持了原始信号中包含的所有模态信息，并同时减少了信号中噪声的影响，因此，以自相关函数构建ARMA模型，可以克服由噪声引起的估计偏差，而不会丢失模态信息。

为了简化，在下面的分析中用x(k)表示实际测量的结构响应。在本研究中，将信号归一化(或标准化)的过程引入到用于信号预处理的集成ARMA模型方法中。执行归一化以便消除加载条件或环境条件改变对结构响应的影响。令xi(t)为来自传感器i的动态响应数据，并且其被划分为不同的段xij(t)，其中i表示传感器编号，j表示分段编号。然后，获得归一化信号

(9)

式中：μij和σij分别为每片段的平均值和标准偏差。

然后，计算归一化信号的自相关函数以建立ARMA模型。适当的ARMA模型阶的定义是基于ARMA模型方法的关键问题之一。在用精确阶数模型评估AR参数时，如果测量被噪声破坏，则不可能获得所有模式。为了获得具有可接受精度的所有模式，需要更高的阶数。然而，这并不意味着模型阶数越高，算法精度越好。对于过建模情况，会产生不必要的更多的伪模式。在这种情况下，拥有一个选择实际模式的标准是必要的。在本研究中，部分自相关函数(PAF)用于估计最佳AR模型阶数。

1.2 基于ARMA模型的马氏距离损伤识别指标

除了系统识别，ARMA估计也可以用于时间序列分类。问题在于如何比较2个ARMA模型，或者找到1个度量来测量ARMA模型之间的距离。

马氏距离是经常用于多变量分析以区分2个序列的分布。马氏距离不同于欧几里德距离，因为它考虑了变量之间的相关性，并且不依赖于观测值的规模。具有协方差矩阵∑的2个向量y和z之间的马氏距离定义如下.

(10)

本研究中，用AR模型参数作为损伤特征向量，定义损伤识别指标DI为Δ(yd，μud；∑ud)与Δ(yud，0；∑ud)的比值，其中μud和∑ud是平均矢量，并且AR模型参数的协方差矩阵对应于未损坏数据集，yd为对应于损坏数据集的AR模型参数向量。该损伤识别指标背后的含义是从损伤情况到无损情况的马氏距离与无损状态到零状态的马氏距离的比率，即它是对由给定结构系统的损坏引起的马氏距离变化的度量。在数学上，度量损伤识别指标DI可以定义为

(11)

因此，损伤识别过程包括2个主要阶段，即训练和监测。训练过程开始于收集来自安装在未损坏状态下结构上所有传感器的结构响应数据。然后，进行分割和归一化过程以预处理原始信号。将预处理的加速度响应的自相关函数(PAF)作为输入数据，以消除对结构响应的噪声影响。部分自相关函数用于估计最佳AR模型阶数。将合理的ARMA模型拟合到每个输入数据序列。所产生的AR系数被用作损伤敏感特征向量。通过求解2个ARMA模型之间的马氏距离，用于损伤检测。

DI的概念实际上是衡量马氏距离变化的一种度量，即由损伤发生引起的振动变化。当发生损坏时，会改变系统的振动模式。对于与某一传感器对应的DI值，不仅包含同一段的局部损伤的影响，而且还包括其他部分的损坏对整个系统振动的影响。从损坏区域附近的传感器检测到的变化应大于其他传感器的变化，因此，需要通过比较整个结构中的所有计算的DI值来建立阈值，仅在DI值大于阈值的位置识别损伤。

研究人员提出了各种定义阈值的方法。例如在Yan等[5]的研究中，完整结构的测量数据假定为正态分布，基于测量数据的平均值和标准偏差，定义阈值。同样，在本研究中，整个隧道系统的DI也被假设为正态分布，以区分由局部损伤引起的异常值，阈值定义为95%的一次置信度的上限。该阈值定义的含义是从某一状态获得的DI值的95%小于该值。因此，具有高于该阈值的相应DI值的传感器很可能对应于具有损坏的位置。假设整个结构系统的损伤指标服从正态分布，则损伤阈值定义为95%的单侧置信上界

(12)

2 基于ARMA模型的盾构隧道结构损伤识别数值分析

建立的盾构隧道实体模型长度为60 m，外径为6 m、管片厚度为0.3 m，隧道外围土体围岩的截面尺寸为46 m×38 m的盾构隧道有限元模型。隧道管片结构采用shell63壳单元，土体围岩采用solid45单元。定义隧道管片的弹性模量为3.45×1010Pa，泊松比为0.2，密度为2 700 kg/m3；定义周围土体围岩的弹性模量为2.5×108Pa，泊松比为0.32，密度为2 200 kg/m3；定义有损伤位置处的隧道管片的弹性模量为(1-损伤大小)×3.45×1010Pa，比如，当损伤大小为10%时，损伤处的弹性模量就设定为0.9×3.45×1010Pa，泊松比为0.2，密度为2 700 kg/m3。有限元模型见图1。

图1 盾构隧道实体有限元模型

地铁列车在行驶过程中对轨道的作用包括2部分，一是列车重量静荷载，二是由于列车运动产生的振动荷载。在本文中，采用激励力函数拟合的方法确定地铁列车荷载[6]，模拟地铁行驶的荷载。

衬砌结构损伤的模拟，通过假定某一单元或者某些单元的不同程度的刚度折减来实现[7]。本文通过壳单元弹性模量的折减来模拟盾构隧道衬砌的损伤。共设置了4个损伤模型和1个无损模型，其中，损伤工况包括单损伤和多损伤，见表1。

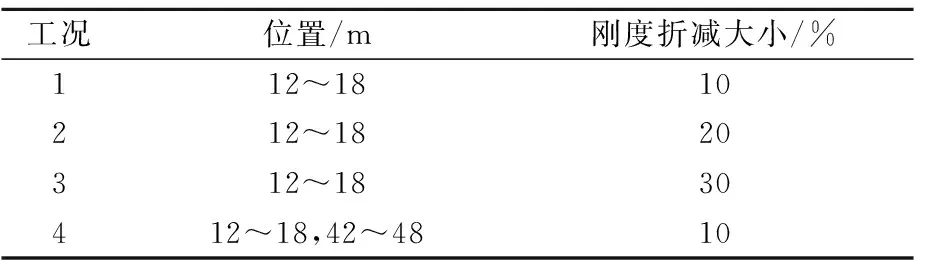
表1 模型损伤工况

求解出盾构隧道-土体围岩有限元实体模型的加速度响应后，将预处理的加速度响应的自相关函数作为输入数据，以消除对结构响应的噪声影响。部分自相关函数(PAF)用于估计最佳AR模型阶数。基于此，将合理的ARMA模型拟合到每个输入数据序列。所产生的AR系数被用作损伤敏感特征向量。通过求解2个模型AR系数之间的马氏距离，从损伤情况到无损情况的马氏距离与无损状态到零状态的马氏距离的比率被定义为损伤识别指标DI，用于损伤检测。结果见图2～图5。

图2 工况1损伤识别图

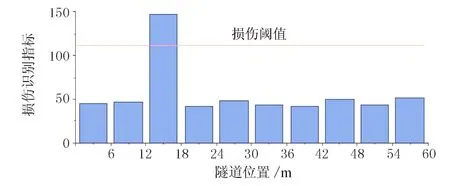
图3 工况2损伤识别图

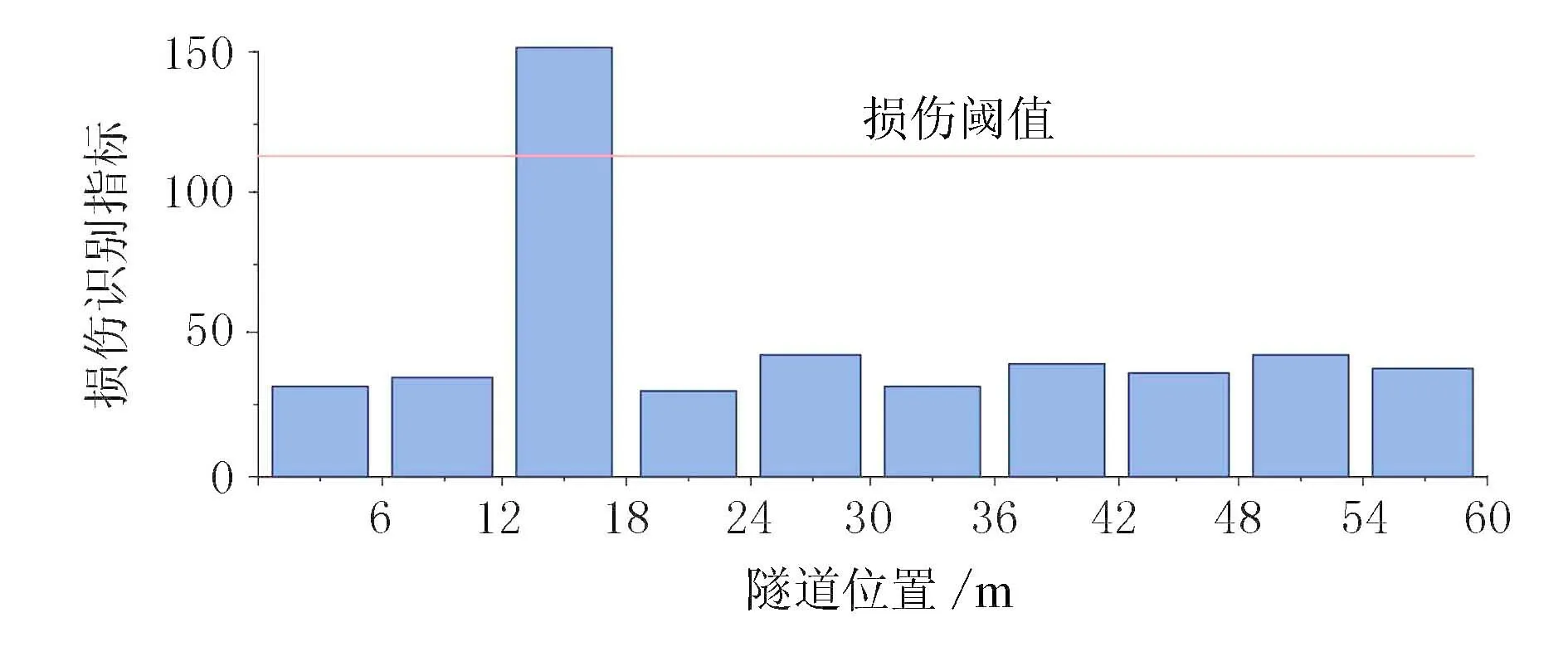
图4 工况3损伤识别图

图5 工况4损伤识别图

工况1～工况3是单损伤工况，工况4是双损伤工况，从图2～图4中可以看出，损伤位置指标值超过损伤阈值，能清楚识别损伤及位置，随着损伤程度的增加，损伤指标值逐渐增大。说明马氏距离指标能有效识别损伤位置和相对损伤程度。

从分析数值模拟的加速度信号的结果来看，马氏距离损伤指标有很好的识别效果，无论是单损伤还是多损伤都能准确识别损伤位置。

3 缩尺隧道模型实验损伤识别分析

由于实际的盾构隧道太大，进行足尺试验非常困难，故采取缩尺试验的方式进一步验证本文提出的损伤识别方法的可行性和有效性。

缩尺模型采用砂箱和管道结合的方式。管道模拟盾构隧道衬砌，砂箱模拟隧道所处的地层环境。铝管一节长14 cm，外径18 cm，内径16 cm，管的两端有法兰状螺栓接头，形状见图6。

图6 铝管模型图

铝管采用螺栓连接，2铝管之间加一圈橡胶垫，螺栓和橡胶垫的设置是为了模拟盾构隧道管片之间的螺栓连接，使其更加符合工程的实际情况。本次缩尺试验隧道结构由30节铝管连接模拟而成。

砂箱采用木板制作，木箱长4 150 cm，宽80 cm，高80 cm，侧面正中间留有直径18 cm的圆形洞口放置管道。砂箱内壁覆盖2 cm厚泡沫板，为了减少振动波的反射和外界振动对管道加速度信号的干扰。木箱中装入砂子模拟土层，试验为了铝管的安装和更换方便，将铝管一半埋入砂中，见图7。

图7 管道放置

本试验中采用小车模型来模拟地铁列车在隧道中的运行荷载。小车模型一共设有6节车厢，每个小车质量为1 kg，2个小车之间用挂钩连接在一起，用恒定转速的电机牵引，从管道一端牵引到另一端模拟列车在隧道中行进。

对完整的铝管切割模拟衬砌结构的损伤。本次试验设置了2 cm×12 cm、2 cm×24 cm的条形缺口。具体切割效果见图8。

图8 条形切口损伤设置

实验共设置了3个工况，如表2所示。每个工况重复试验5次，采集加速度信号，以避免单次采集的误差。本次试验共布置了8个加速度传感器，分别在第2，6，10，14，18，22，25，28号铝管上，采样频率定为500 Hz。

表2 工况设置

图9～图11为各工况下的损伤识别结果图。

图9 缩尺实验工况1损伤识别图

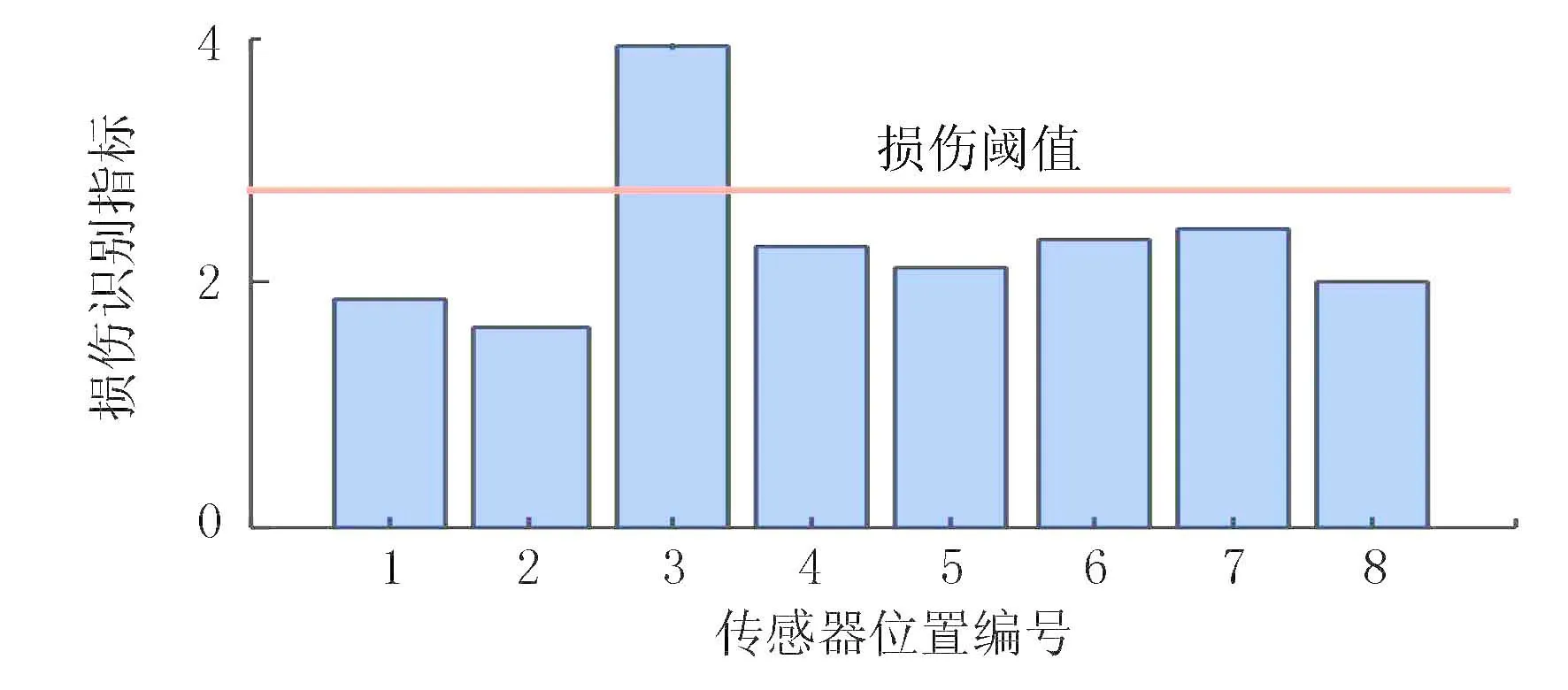
图10 缩尺实验工况2毁损伤识别图

图11 缩尺实验工况3损伤识别图

工况1和工况2的损伤位置设置在缩尺盾构隧道结构中第10节铝管。图9、图10为工况1和工况2应用ARMA模型方法得出的损伤识别图。图9和图10显示在第3个加速度传感器位置处的DI值超过了阈值，而且为最大值，说明在第3个加速度传感器位置的缩尺节段发生了损伤。图9和图10表明，基于ARMA模型的损伤识别方法可顺利的识别损伤位置，并且损伤程度也能通过指标值的大小呈现。

工况3的损伤位置设置在缩尺盾构隧道结构中第10和25节铝管，损伤大小分别为8%和5%。图11为工况3应用ARMA模型方法得出的损伤识别图。图11显示在第3个加速度传感器和第7个加速度传感器位置处DI超过了阈值，说明在第3个加速度传感器和第7个加速度传感器位置出现了损伤。可以看出，第3个加速度传感器对应位置的DI值大于第7个传感器对应位置的DI值，验证了ARMA模型方法对损伤程度的敏感性。

4 结语

利用基于ARMA模型的结构损伤识别方法，对隧道结构进行了损伤识别，理论计算结果和数值计算结果均表明该方法可有效识别盾构隧道结构损伤位置和程度。