三维角度域网络干扰的空间选择特性

杜得荣，曾孝平，简 鑫，杨 凡,2，陈 礼

(1. 重庆大学 通信工程学院，重庆 400044；2. 重庆金美通信有限责任公司，重庆 400044)

大规模无线通信网络(如车联网、无线传感器网络和密集部署网络等)由数量众多的节点构成，对稀缺的频谱资源需求极大． 高密度频谱空间复用是提高频谱利用率的主要手段，然而这会带来严重的网络干扰[1-2]． 三维智能天线和波束赋形技术的快速发展为解决网络干扰问题提供了有效手段，而网络干扰的空间选择特性对智能天线和波束赋形的设计和性能评估有着重要影响． 因此，在三维空间角度域，对网络干扰的统计特性进行研究可为干扰避免和消除技术提供理论支撑．

目前，对网络干扰进行建模和分析的文献较多，但大多文献是基于随机几何理论，分析接收端总干扰包络或功率的大小及概率密度[3-4]，而对干扰空间选择特性建模和分析的研究很少． 由于大规模无线通信网络包含大量空间分离节点，任意接收端的干扰信号数目众多，干扰信号可类似于信道建模中多径散射信号，因此，空间多径信道建模理论可为网络干扰统计特性的研究提供重要视角． 文献[5]提出了二维多径成型因子理论，用来描述多径衰落角度域空间选择特性，即用三个成型因子(角扩展、角收缩和最大衰落方位角方向)对本地区域的任何非全向的多径波束分布进行定量分析，具有物理意义明确，表述简单的优点． 文献[6]基于二维多径成型因子理论提出了三维多径成型因子理论，运用角扩展、俯仰角收缩、45°俯仰角收缩、方位角收缩、45°和0°俯仰角下最大衰落方位角方向六个因子表征信道的角度域空间选择特性． 二维及三维多径成型因子理论为研究大规模网络干扰的空间选择特性提供了有力工具，文献[7-8]就基于二维成型因子理论对二维空间网络干扰进行了角度域建模，并分析了干扰的统计特性． 由于通信网络各节点的高度不同，信号传播也会受到三维空间中的散射体散射，因此，网络干扰功率分布于三维空间中． 然而，已有文献尚未就三维角度域网络干扰模型及其统计特性展开研究．

针对已有文献的研究不足，笔者面向包含大规模空间分离节点的无线通信网络，提出一个三维高斯干扰空间分布模型，并给出相应的干扰功率角度谱密度函数． 然后，基于三维成型因子理论，推导出了干扰关键空间统计特性的闭合表达式． 最后，仿真分析了三维角度对干扰功率角度谱密度函数和关键空间统计特性的影响，研究结果可简化三维智能天线和波束赋形技术的设计和评估．

1 三维高斯干扰空间分布模型和干扰功率角度谱密度

1.1 三维高斯干扰空间分布模型

图1 三维高斯干扰空间分布模型

图1展示了接收端干扰来波的功率分布，RX为接收端;干扰者(基站或其他终端节点)与RX具有视距路径时，I为干扰者，干扰者与RX无视距路径时，I为干扰信号到达RX前的最后一个散射体;S为干扰所分布的三维空间(灰色区域);α∈ [0，2π]为干扰来波方位角，β∈ [0，π/2]，为干扰来波俯仰角;r为I到RX的距离;σ为高斯分布标准差，根据高斯分布3σ原则，r的最大有效值为3σ．

三维高斯干扰空间分布模型基于以下假设和设定:

(1) 距离越远的干扰信号受到的大、小尺度衰落越严重，即距离RX越近，干扰信号功率影响越大，因此，干扰来波功率在三维空间距离上不服从均匀分布[9]，假设其服从以RX为中心的高斯分布[10]．

(2) 在实际通信中，水平和竖直方向的干扰者(或干扰散射体)分布是不同的，一般来说，仰角越低，干扰者(或干扰散射体)越多，影响越大，因此，高斯分布的标准差需要在水平和竖直方向分别控制．

(3) 由于大规模网络中节点多且密度高，因此，假设干扰来波数目趋于无穷．

(4) 假设各个干扰衰落信号服从瑞利分布或莱斯分布，由文献[8, 11]可知，多个瑞利分布或莱斯分布的和分布可近似于一个Nakagami-m分布[12]，因此，假设总干扰信号服从Nakagami-m分布．

1.2 干扰功率角度谱密度

假设干扰来波功率在三维空间S中服从高斯分布，其表达式为

(1)

通过雅可比式，将式 (1) 的笛卡尔直角坐标系转换为球坐标系[13]，即

(2)

式 (2)为(r，α，β)的联合分布，若对r进行积分，则可得(α，β)的联合分布，即干扰功率角度谱密度，即

(3)

由式(3)可得干扰功率方位角边缘分布和俯仰角边缘分布分别为

则干扰水平方向和竖直方向分布是相互独立的，即pG(α，β)=pG(α)pG(β)．

又因为干扰功率俯仰角边缘分布积分为1，即

(4)

2 干扰空间统计特性

2.1 非规范复球谐系数和三维成型因子

(5)

(6)

2.2 衰落率方差

由于平稳过程的导数均值为零，因此，均方导数即为度量干扰衰落速率的最简单统计量，而平稳过程的均方导数为变化率的方差，即衰落率方差，可表示为[6]

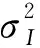
2.3 空间相关函数和相关距离

广义平稳过程信号包络r的空间相关函数可由麦克劳林级数表示[14]，即

其中，rc为空间距离，Vm(r)为Nakagami-m分布的方差． 而空间相关函数又可近似为指数函数及其麦克劳林级数[5]，即

(9)

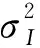
(10)

其中，Γ(·)为Gamma函数，m为Nakagami-m分布的形状因子． 若定义相关函数为 exp(-1) 时的rc为相关距离Dc，则Dc(α，β)= {2PT[mΓ2(m)- Γ2(m+ 1/2)]}1/2/ [m1/2Γ(m)σI(α，β)]．

3 仿真分析

下面主要仿真分析三维空间角度对干扰功率角度谱密度函数和关键空间统计特性的影响．针对常见的 2.4 GHz 频段(即λ= 0.125 m) 通信，为便于分析，将平均接收干扰功率设置为PT=1． 在实际通信中(如市区车车通信)，有效干扰者的竖直高度有限，高斯竖直方向标准差设置为σβ= 5 m，即有效干扰者最大高度为 15 m． 通过调整形状因子m的值，Nakagami-m分布能够模拟严重、适中、轻微到无衰落的信号衰落场景，这里假设干扰信号衰落适中，形状因子设置为m=2．

3.1 干扰功率角度谱密度

图2展示了不同高斯水平方向标准差σα和三维均匀干扰空间分布下，俯仰角对干扰功率角度谱密度的影响．在实际通信中，有效干扰者的水平距离可能较远，因此，图2考虑了不同σα带来的影响． 式 (3) 中，俯仰角的单位为弧度，为便于描述，图2中俯仰角的单位采用度． 若干扰来波功率在半球体中服从以RX为中心的均匀分布，按1.2节方法，此时的干扰功率角度谱密度可计算为 cosβ/ (2π)． 由图2可知，σα越大，干扰功率越集中于更小的仰角范围，然而σα≥ 400 m 时，各干扰功率角度谱密度曲线趋于重合，这说明由于较大的路损和遮挡，水平距离 3σα≥ 1 200 m 之外的干扰影响已经很小; 在不同σα下，各干扰功率角度谱密度曲线随着仰角的增大而急剧降低，在仰角为15°时，各干扰功率角度谱密度曲线几乎降低到零; 在三维均匀干扰空间分布场景下，干扰功率角度谱密度曲线随着俯仰角增大而极为缓慢的降低，不能很好地表征实际通信中竖直方向有效干扰者少、影响小的规律． 以上干扰空间选择特性可为智能天线和波束赋形技术的设计提供参考，使天线和波束避开主要干扰以提高系统性能．

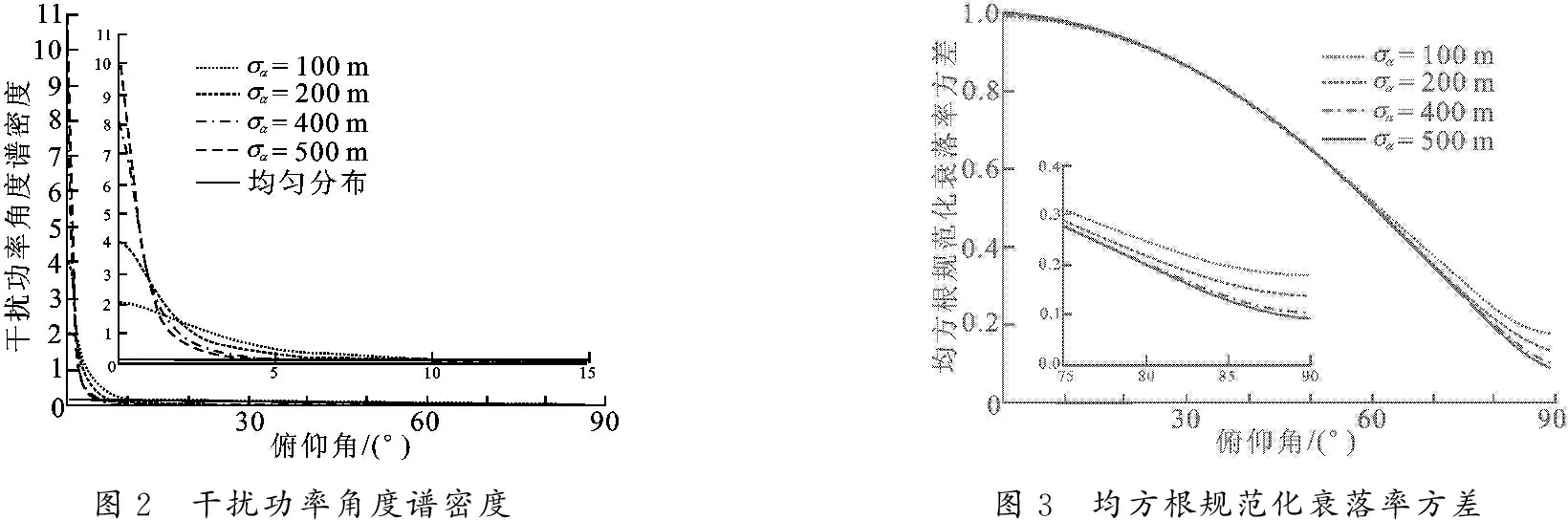
图2 干扰功率角度谱密度图3 均方根规范化衰落率方差

3.2 三维成型因子和衰落率方差

3.3 空间相关函数和相关距离

图4展示了高斯水平方向标准差σα=400 m时，不同空间间隔距离和俯仰角对空间相关函数的影响． 由图4可知，间隔距离和俯仰角对空间相关函数都有决定性影响: 在 0°～ 60°俯仰角范围内，间隔距离的影响占主导地位，且间隔距离rc≥ 0.5λ时，空间相关函数趋近于0; 在 60°～ 90°俯仰角范围内，俯仰角的影响占主导地位，且俯仰角趋近于90°时，即使间隔距离rc=λ，空间相关函数仍然较大． 图5展示了高斯水平方向标准差σα= 400 m时，不同俯仰角对相关距离的影响． 同样，俯仰角对相关距离影响很大，尤其是俯仰角趋近于90°时． 空间相关函数和相关距离是度量信号空间选择特性的重要指标，其可指导多天线阵列间隔的优化设计．由图4和图5可知，多天线阵列阵元间的间隔设置应随仰角的变化而变化，即为减少干扰相关性的影响，低仰角时需较小的间隔距离，高仰角时需大的间隔距离．综合图2～图5可知，仰角为15°时，干扰功率角度谱密度几乎降低到零，均方根规范化衰落率方差较大，空间相关性和相关距离也较小，因此，15°仰角也是合适的天线阵列朝向．

图4 空间相关函数图5 相关距离

4 结 束 语

针对车联网、无线传感器网络和密集部署网络等干扰受限的大规模网络，提出了一个三维高斯干扰空间分布模型，推导出了干扰功率角度谱密度函数和关键空间统计特性的闭合表达式，并仿真分析了三维空间角度对干扰功率角度谱密度函数和关键空间统计特性的影响． 仿真分析表明，俯仰角是网络干扰空间选择特性的决定性影响因素，其中15°仰角处干扰功率角度谱密度几乎为零，均方根规范化衰落率方差较大，空间相关性和相关距离也较小，这一特性可用于三维智能天线和波束赋形技术的设计和评估．