星载伞状可展开天线支撑肋结构优化
2018-10-11郑士昆李洲洋
王 波,郑士昆,李洲洋,谢 卓
(1. 西安空间无线电技术研究所,陕西 西安 710100;2. 西北工业大学 机电学院,陕西 西安 710072)
伞状可展开天线作为一种新型可展开卫星天线结构形式,具有结构简单、可靠性高、形面精度可调整和制造成本低等优点,近年来成为可展开卫星天线研究的热点,受到各国航天机构的大力研究[1-2].文献[3]提出了一种紧凑的伞状天线结构,并分析了空间环境下的天线热变形.文献[4]建立了大型伞状可展天线支撑肋自由振动运动方程,并进行了模态分析.文献[5]建立了伞状天线反射面索网模型,得到了天线形面误差的变化规律.文献[6]分析了在考虑预紧力时,伞状天线动力学的振动特性.文献[7]研究了伞状天线转动副的可靠性.文献[8]研究了伞状天线张力索在温度及重力作用下的稳定性.文献[9]运用有限元分析方法对径向支撑肋进行了热变形分析.综上所述,现有研究内容多集中于天线展开原理、整体结构设计及索网分析方面,缺少针对径向支撑肋的结构优化研究.
径向支撑肋作为伞状天线最重要的结构件,同时受到刚度和质量两方面的约束.支撑肋在反射面和张力索拉力作用下会产生弯曲变形[10].若减小结构尺寸、减轻质量,会导致支撑肋刚度不足,难以保证反射器形面精度; 增大结构尺寸,增加刚度,减小弯曲变形,会导致质量增加.因此,在进行支撑肋结构设计时,需要研究如何在保证支撑肋刚度、使其不产生过大变形的条件下,尽量减小支撑肋的质量.
为此,需要分析天线工作时支撑肋的受力状态,采用结构优化设计方法,建立支撑肋结构优化模型,对伞状天线支撑肋进行结构优化,以获取满足要求的优化结构参数,为伞状天线结构设计提供依据.
1 支撑肋结构及受力分析
伞状可展开天线主要由安装在环形基座上的抛物线状径向支撑肋、连接相邻两肋的柔性张力索以及覆着于张力索上的柔性金属反射面组成.伞状天线结构如图1所示.

图1 伞状可展开天线图2 伞状可展开天线张力索结构
柔性张力索包括前张力索、后张力索及纵向张力索.前、后张力索两端固定于支撑肋上,中间通过纵向张力索相连接,如图2所示.金属反射面覆着于前张力索上.通过调整张力索的空间位置,可以使反射面近似形成所需的抛物面形状,以满足形面精度要求.

图3 天线支撑肋受力及变形

2 支撑肋结构的优化建模
在张力索集中拉力和反射面均布拉力的作用下,天线支撑肋会产生一定的弯曲变形.若变形量过大,会造成张力索及反射面松弛,导致形面精度下降,使天线无法正常工作[13].因此,需要在保证支撑肋变形满足设计要求的前提下,使支撑肋具有尽量小的质量,以满足航天应用需求.
为使支撑肋具有足够的刚度,同时考虑方便加工和安装,通常将支撑肋的截面取为图4(a)所示的空心矩形.同时考虑支撑肋由根部到端部所受弯矩逐渐减小,可以采用变截面等壁厚的结构形式减轻质量,即支撑肋根部采用较大的截面尺寸,而端部采用较小的截面尺寸,如图4(b)所示.
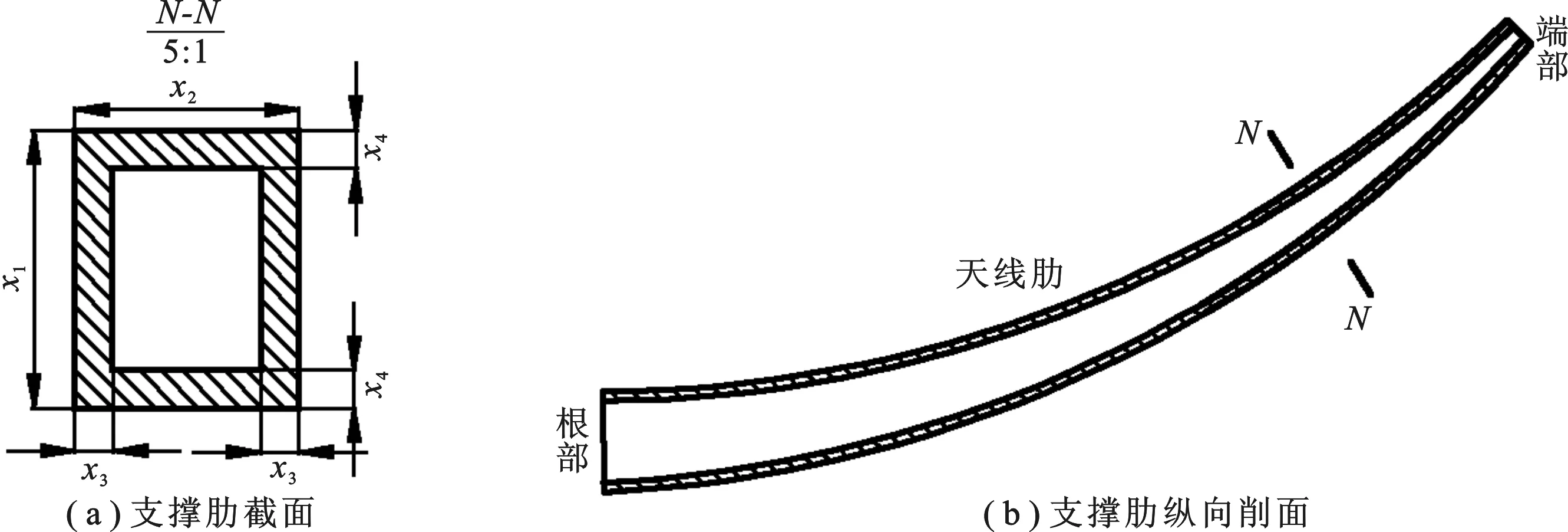
图4 支撑肋结构
根据图4所示的支撑肋结构,在满足变形要求的前提下,建立以支撑肋质量最小为优化目标,以支撑肋根部截面高度、根部截面宽度、纵向壁厚、横向壁厚以及天线端部与根部截面尺寸比值为设计变量的优化模型,其表达式为
(1)
其中,f(x)为支撑肋质量;v(x)为支撑肋单元体积;ρ为支撑肋材料密度;g1(x)为支撑肋端部变形约束;g2(x)为支撑肋端部高方向几何约束,保证支撑肋端部高方向壁厚;g3(x)为支撑肋端部宽方向几何约束,保证支撑肋端部宽方向壁厚;δ(x)为支撑肋端部变形; [δ]为支撑肋端部许用变形;x1为肋根部截面高度;x2为肋根部截面宽度;x3为肋根部截面宽方向壁厚;x4为肋根部截面高方向壁厚;x5为肋端部与根部截面尺寸的比值;ai和bi分别为变量xi取值范围的下限和上限; 设计变量x= (x1,x2,x3,x4,x5)的取值范围由天线实际结构及需求确定.
3 支撑肋优化模型求解
针对文中所建立的优化模型,分别采用蒙特卡罗法[14-15]和复合形法[14,16]进行优化求解.
3.1 蒙特卡罗法优化求解
采用蒙特卡罗法对支撑肋优化模型进行求解时,需要解决可行初始点选取、可行搜索方向计算和搜索步长取值等关键问题.
初始点可在满足约束条件下采用随机法产生.基于设计变量xi∈[ai,bi],i=1,2,…,5,计算xs的各分量:
xi=ai+qi(bi-ai) ,i=1,2,…,5 ,
(2)
其中,qi为在区间(0,1)内的均匀分布的随机数.
若随机点xs不满足约束条件,则需要重新生成随机数,直至xs满足约束条件,并将其视作初始点.
在确定可行搜索方向时,采用随机数rki(k=1,2,…,200,i=1,2,…,5)生成200个随机单位向量ek,ek可表示为
按步长α0生成200个随机点,则有
xk=x0+α0·ek,k=1,2,…,200 .
从xk中找出满足约束条件的目标函数值最小点的可行点xl,若f(xl)≥f(xs),则需缩小步长α0,重新生成xk,直至f(xl) 按照可行搜索方向xs→xl,将xl作为新的起始点xs,进行迭代搜索.迭代时步长α按下式计算:αw+1=ταw,其中,αw+1为第w+1 步迭代步长;αw为第w步迭代步长; 初始步长取α0= 0.1;τ为步长系数,加速进时取1.3,加速退时取0.7. 其中,ε1为目标函数值计算精度,取10-6;ε2为设计变量计算精度,取10-3. 采用复合形法进行优化求解的关键是解决初始复合形构建和复合形搜索方法问题. 取复合形顶点数n为优化变量数加1,即n=6.产生初始复合形时给定1个可行顶点,并采用式(2)所示的随机法产生其余n-1 个顶点.对于随机点中的非可行顶点xp按式(3)反复变换,直至满足约束条件,生成初始复合形,即 xp=xo+0.5(xp-xo) ,p=1,2,…,m, (3) 其中,m为非可行顶点数,xo为所有可行顶点的几何中心. 利用反射法进行复合形形状优化时,首先,要计算并比较复合形各顶点的目标函数值,寻找最坏点xh,即 f(xh)=max{f(xq),q=1,2,…,n} . 然后,计算除点xh外的其余顶点的中心点xc,以xh→xc为搜索方向,寻找反射点xr,即 xr=xc+αt(xc-xh) , 其中,αt为反射系数,此处取αt=1.3. 通过不断调整反射系数αt的取值,寻找反射点xr,直到满足反射成功条件: 当复合形所有顶点与中心点的均方差满足 (4) 收敛条件时,迭代结束.其中,xd为复合形n个顶点的几何中心;ε3为目标函数值计算精度,取10-6. 天线支撑肋采用碳纤维材料,材料密度ρ=1.8×10-3g/mm3,弹性模量E= 9.0 GPa.支撑肋原始结构数据如表1所示. 表1 支撑肋结构参数mm 基于表1数据计算,得到支撑肋质量为691.8 g.考虑天线支撑肋实际工作情况,忽略重力影响,计算在给定载荷下的端部变形为 2.98 mm.因此,限定优化模型中肋端部可用变形量近似为 3.0 mm.考虑天线支撑肋强度条件、支撑肋间互不干涉条件、碳纤维加工工艺以及实际装配要求等约束,确定优化模型中各参数取值范围如表2所示. 表2 支撑肋参数取值范围mm 采用与原始结构相同的载荷,基于表2给定的优化变量取值范围,分别用蒙特卡罗法和复合形法分别对支撑肋结构参数进行优化.为了对比分析,增加了对x5= 1.0时的等截面支撑肋结构优化算例.计算结果如表3所示. 表3 支撑肋结构优化结果 对比表3的支撑肋优化结果与表2给定的变量取值范围可以发现,在进行支撑肋结构优化时,不论采用等截面优化还是变截面优化,肋根部截面宽度x1、肋纵向壁厚x3和肋横向壁厚x4都取到了取值范围的下限,而肋根部截面高度x2则取到了较大的值.这表明宽度和壁厚对于支撑肋抵抗弯曲变形的能力贡献不大,截面高度才是影响支撑肋抵抗弯曲变形能力的关键因素.要增强支撑肋的弯曲刚度,首先应考虑增加肋的截面高度; 同时,在满足结构和功能要求的前提下,尽量减小宽度和壁厚以减轻质量. 从表3数据可以看出,优化后支撑肋的质量明显减轻:采用等截面结构优化后,支撑肋质量较优化前减少了约38.770%; 采用变截面结构优化后,支撑肋质量较优化前减少了约50.410%.相比等截面结构形式,采用变截面结构优化的效果更为理想,在进行结构设计时应优先考虑. 从表3的计算结果可以看出,蒙特卡罗法和复合形法优化计算结果是一致的.两种优化方法的计算收敛过程分别如图5和图6所示.分析收敛过程可以发现,蒙特卡罗法在计算过程中迭代误差有振荡现象,直到 938 s 才得到计算结果; 复合形法的迭代误差则持续收敛,在 167 s 时就获得了优化结果.相比蒙特卡罗法,复合形法表现出更快的收敛速度和更强的稳健性.因此,对于此类结构进行优化时,应优先选用复合形法进行问题求解. 图5 蒙特卡罗法计算收敛过程图6 复合形法计算收敛过程 文中以伞状可展开天线支撑肋为研究对象,通过对支撑肋的结构和受力分析,建立了支撑肋优化设计模型,并通过研究两种优化求解算法,得到了优化设计结果.通过分析可以看出,优化后支撑肋减重效果较为显著.通过对结构参数优化结果的分析发现:增加支撑肋截面高度和采用变截面结构是支撑肋优化的主要方向.文中的优化方法也可以为其他同类型结构件的优化设计提供有益的借鉴和参考.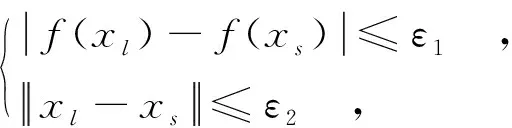
3.2 复合形法优化求解
4 优化计算结果及分析




5 结 束 语
