高低轨异构双基地SAR改进CS成像算法

王跃锟，索志勇，李真芳，张金强，张庆君

(1. 西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071；2. 北京空间飞行器总体设计部，北京 100094)

地球同步轨道(Geosynchronous Earth Orbit，GEO)卫星合成孔径雷达(Synthetic Aperture Radar，SAR)的地面覆盖范围广，时间分辨率高，但空间分辨率低[1]; 而以地球同步轨道卫星作为主动照射源，低地球轨道(Low Earth Orbit，LEO)卫星被动无源接收地面散射信号的双/多基协同体制，可实现高信噪比和高时空分辨率[2]，且灵活性强、成本低、抗摧毁和抗干扰能力强，可实现轻型化、模块化及商业化．因此，GEO-LEO双基合成孔径雷达(Bistatic SAR，BiSAR)体制与当前星载合成孔径雷达系统相比，可显著提高对地观测能力，具有广阔的应用前景[3]．然而，目前国内外对该体制的研究尚处于起步阶段，仍面临许多技术难题[4]．

星载合成孔径雷达系统的诸多应用都是以合成孔径雷达图像为基础的，因此研究适用于GEO-LEO BiSAR系统的成像处理技术势在必行．文献[5]针对地球同步轨道单基合成孔径雷达系统的“走-停”假设进行了分析并给出补偿方法，然而由于GEO-LEO双基合成孔径雷达系统中接收机的速度较快，文献中的直线轨迹假设并不成立．此外，该系统在复杂双基成像几何关系下，回波信号在距离向和方位向都具有较强的空变性．文献[6]提出一种大斜视下的同轨双基合成孔径雷达成像方法，然而该体制下不存在方位调频率空变问题．文献[7]提出了一种机载双基频域成像方法，但该方法只适用于直线轨迹，且成像范围较小．文献[8]提出了一种基于级数反演的双基成像方法，然而其未考虑方位调频率空变和保相性等问题．因此以上方法均不适用于GEO-LEO双基合成孔径雷达系统．

为解决上述问题，笔者针对GEO-LEO双基合成孔径雷达系统的成像处理技术做了深入研究，提出一种适用于该系统的基于二维时域扰动的改进线性调频变标(Chirp Scaling，CS)成像方法．首先，建立双基观测几何，推导出非“走-停”假设下的等效信号模型;然后，通过时域扰动的方式校正回波二维空变性，并对残余相位进行补偿;最后，通过仿真实验验证了该算法的有效性．

1 GEO-LEO双基合成孔径雷达系统信号模型

1.1 空间观测几何

图1 GEO-LEO双基合成孔径雷达系统对地观测几何示意图

建立GEO-LEO双基合成孔径雷达系统的观测几何，如图1所示．坐标系为目标本体坐标系，即以目标位置为原点，目标所在的地球表切面为XOY平面，Z轴垂直于XOY平面指向地球表面外法线方向，X轴为低地球轨道卫星波束中心视线在XOY面的投影方向，Y轴由右手法则确定．地球同步轨道卫星在t时刻发射信号，此时高、低轨卫星的位置矢量分别为PG(t)和PL(t)，速度矢量分别为VG(t)和VL(t)，斜距矢量分别为RG(t)和RL(t); 经时延τ1后，信号到达目标位置，此时低地球轨道卫星位置、速度和斜距矢量分别为PL(t1)、VL(t1)和RL(t1); 信号经目标反射，时延τ2后到达PL(t2)位置，此时低地球轨道卫星速度和斜距矢量分别为VL(t2)和RL(t2)．θG和θL分别为高、低轨卫星入射角，φ为双基角在XOY面的投影，即双基位置投影角，ψ为双基速度投影角．

1.2 信号模型

在GEO-LEO双基合成孔径雷达系统中，由于信号收发时延长、接收机速度快，导致“走-停”假设不成立，且在信号传播期间低地球轨道卫星速度矢量变化不可忽略．

设低地球轨道卫星在t时刻的加速度为aL(t)，则非“走-停”假设下的目标到接收机的距离为

(1)

其中，c为电磁波传播速度．由于信号在目标到低地球轨道卫星间的传播时延τ2极短，该时间段内低地球轨道卫星速度的变化可忽略，因此可将式(1)重写为

(2)

将式(2)在τ2处进行泰勒展开，并忽略高阶微小项，可得

(3)

根据式(3)，最终求得在某一时刻t下，非“走-停”假设下的双程精确斜距模型为

(4)

为验证式(4)的斜距模型，在X波段下采用表1参数进行仿真．卫星工具包(Satellite Tool Kit，STK)中观测几何如图2(a)所示，斜距误差如图2(b)所示．在“走-停”假设下引入的斜距误差随时间呈线性变化，在 2 s 时间内引入约 20 m 的斜距误差；而式(4)的非“走-停”斜距模型引入的最大相位误差只有2.4°，可忽略不计．

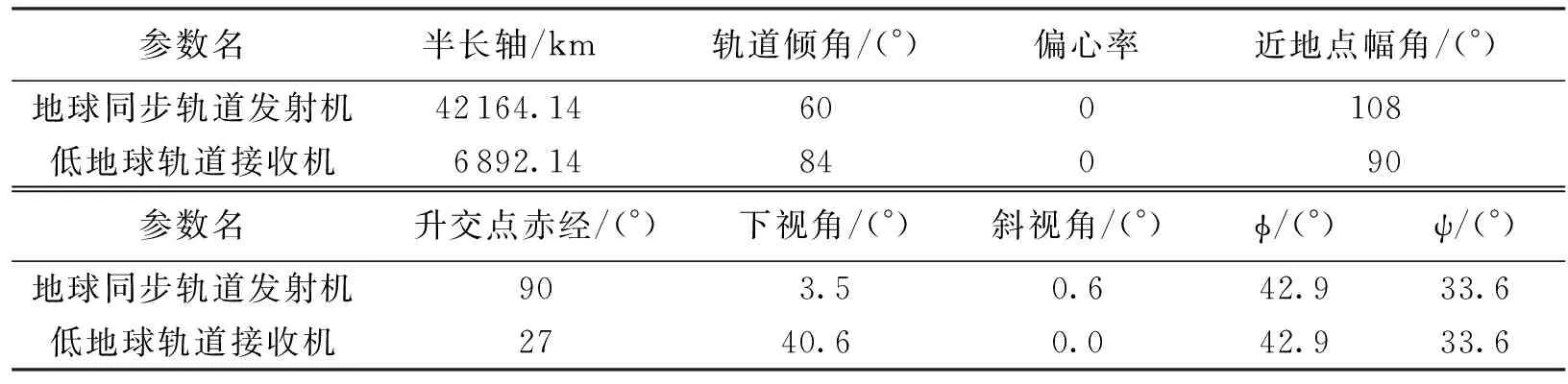
表1 GEO-LEO双基合成孔径雷达系统的轨道参数

图2 STK软件中的高低轨观测几何示意图和模型的误差曲线

在GEO-LEO双基合成孔径雷达系统的异构双基模型下，由于高低轨卫星轨迹非直线、非平行、非等速等原因，采用式(4)斜距模型进行成像算法的推导是非常困难的．考虑到GEO-LEO双基合成孔径雷达系统的合成孔径时间与低地球轨道单基合成孔径雷达的相当(秒级)，短时间内地球同步轨道卫星斜距变化很小，可采用最小二乘算法[9]对式(4)进行等效单基拟合．等效后的单基斜距模型为

(5)

其中，Ve为单基等效速度，θe为等效斜视角，Re为等效波束中心斜距．仍采用表1中的仿真参数，在非“走-停”假设下等效单基斜距模型引入的相位误差如图2(c)所示，其最大相位误差不超过3°，可忽略．

根据式(5)和驻定相位原理[10]，GEO-LEO双基合成孔径雷达系统单点回波信号的距离-多普勒域表达式为

其中，σ为复常数，λ为波长，pr(·)和Wa(·)分别为信号距离向和方位向包络，R0为目标最近斜距，Km和D(fa，Ve)分别为多普勒域信号的调频率和徙动因子．Km和D(fa，Ve)的表达式为

(7)

其中，Kr为发射信号的调频率．根据推导的GEO-LEO双基合成孔径雷达系统斜距模型，笔者建立了单点目标的等效距离-多普勒域信号模型．但对于场景中的不同目标，由于真实双基斜距历程变化，造成其等效速度不同．

传统的线性调频变标成像算法[11]是针对单基合成孔径雷达体制提出的，其首先对距离徙动(Range Cell Migration，RCM)进行补余校正和一致校正，再对距离向和方位向分别做匹配滤波，实现二维合成孔径雷达聚焦．然而，这是以场景中所有目标的等效速度相同为前提的，因此并不适用于GEO-LEO双基合成孔径雷达系统．

2 GEO-LEO双基频域成像处理方法

在GEO-LEO双基合成孔径雷达系统观测模型下，场景中不同目标的等效速度不同，导致传统的线性调频变标算法无法精确聚焦．笔者针对该问题提出一种基于二维时域扰动的改进线性调频变标成像算法，可校正由于等效速度不同造成的距离徙动空变和方位调频率空变，实现高分辨率宽幅场景的良好聚焦效果，且具有较好的保相性能．

2.1 距离向时域扰动

根据式(6)，以中心斜距目标为参考，GEO-LEO双基合成孔径雷达系统精确的距离徙动差量可表示为

ΔR=2{R0[1/D(fa，Ve)-1/D(fref，Ve)]-Rref[1/D(fa，Vref)-1/D(fref，Vref)]} ,

(8)

其中，Rref和Vref为参考目标的斜距和等效速度，fref为参考多普勒频率．仍采用表1中的参数，30 km× 30 km 场景的最大距离徙动差量如图3(a)所示．经计算，ΔR在每一距离门内所有的方位位置满足

max|2R0[1/D(fa，Ve)-1/D(fref，Ve)-1/D(fa，V)+1/D(fref，V)]|≪δr/4 ,

(9)

其中，V为某一距离门内方位中心处目标的等效速度，δr为距离分辨单元(取1 m)．因此，ΔR随方位向变化很小，可忽略[12]．此外，由图3(a)可知，ΔR与R0呈线性变化，且在高分辨时不可忽略．根据线性调频变标原理[12]，可采用时域扰动的方式进行补余距离徙动校正．将式(6)乘以如下线性调频信号:

H1(τ)=exp{jπKp[τ-(2Rref/c)/D(fa，Vref)]2} ,

(10)

其中，Kp为该信号的调频率．再在距离频域乘以如下匹配滤波器:

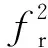
(11)

经上述频率调制和距离向的脉冲压缩后，与参考目标位置间隔Δr的目标将产生平移，移动量为

(12)

不难发现，该移动量即为补余距离徙动值，即Δrmove=ΔR．将式(8)写为

ΔR≈2m(R0-Rref)[1/D(fa，Vref)-1/D(fref，Vref)] ,

(13)

其中，m为常数，可通过式(8)与式(13)线性拟合得到．这样，可求得变标信号式(10)的调频率为

Kp=mKm[D(fref，Vref)/D(fa，Vref)-1]/[(1-m)D(fref，Vref)/D(fa，Vref)+m] ．

(14)

此时信号具有一致的距离徙动．需要说明的是，时域变标会引入二次残余相位[13]，可在距离向处理后予以补偿．一致距离徙动校正函数H3和二次残余相位补偿函数H4分别为

(15)

2.2 方位向时域扰动

由于在同一距离门内目标的等效速度随方位向空变严重，故无法采用统一的匹配滤波器聚焦．针对该问题，此处通过数值拟合的方式，给出一种基于时域调频率扰动的方位向非线性处理方法．

图3 30 km场景目标的最大距离徙动差量和二次相位误差值曲线

对于每一距离门Rbi，以方位中心时刻tref为参考，通过双基合成孔径雷达定位的方式设置一组方位ti时刻的目标，可计算得到该距离门内不同方位位置与方位向参考中心位置目标的方位调频率差为

ΔKa(Rbi，ti)=Ka(Rbi，ti)-Ka(Rbi，tref) ，

(16)

EQPE=π ΔKa(Rbi，ti)(Ta/2)2,

(17)

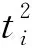
H5=exp[-j2π(n1t3/6+n2t4/12)] ．

(18)

将距离向处理后的信号在方位时域乘式(18)，使每一距离门内目标有一致的方位调频率，再在距离-多普勒域采用下述方位匹配滤波器，完成方位压缩:

H6=exp[-j4πR0D(fa，V)/λ] ．

(19)

此外，由式(18)可知，方位扰动函数是t的高阶多项式，因此在校正调频率空变的同时会引入一些给成像质量带来负面影响的相位误差．对方位时间为t的目标，将式(18)在其合成孔径时间内进行泰勒展开，可获得残余相位．首先，根据时频对应关系，每一距离门的残余高次相位误差补偿公式为

H7=exp{j2π[n1(fa/Ka(Rbi，tref))3/6+n2(fa/Ka(Rbi，tref))4/12]} ．

(20)

其次，考虑到算法的保相性，需在时域补偿残余常数相位，补偿公式为

H8=exp[j2π(n1t3/6+n2t4/12)] exp[-jπ(n1t2/2+n2t3/3)2/Ka(Rbi，yref)] ．

(21)

2.3 算法流程

笔者针对GEO-LEO双基合成孔径雷达系统提出了一种基于时域扰动的改进型线性调频变标成像算法，完整的算法流程如图4所示．

图4 GEO-LEO双基合成孔径雷达系统的改进型线性调频变标成像算法

3 仿真实验结果

为验证笔者提出的GEO-LEO双基合成孔径雷达成像算法，采用表1和表2中的参数，设置 28 km× 28 km 场景下均匀布置的 5×5 点阵目标进行仿真验证，其在地面场景中的分布如图5(a)所示，成像结果如图5(b)所示，部分点目标的成像质量指标如表3所示．从成像结果可看出，各点目标在距离向都可实现很好的聚焦，峰值旁瓣比约为 -13.25 dB，积分旁瓣比约为 -10.28 dB; 方位向越靠近场景中心，聚焦效果越好，场景边缘目标旁瓣会有轻微抬高，但都低于 -11.5 dB，这可在成像处理中通过加窗的方式予以降低; 各点目标聚焦后的残余相位误差最大不超过8°，可满足后续处理(如干涉测高)的需求．

表2 系统参数

表3 部分点目标的成像质量指标

需要说明的是，由于双基成像几何影响，使场景中同一距离上的不同目标，在成像结果中处于不同距离门，可通过几何校正的方式予以纠正[13]，但这超出笔者的研究范围，这里不再赘述．

图5 28 km×28 km场景下5×5点阵目标的分布图及成像结果

此外，部分点目标的传统线性调频变标成像方法[11]与笔者提出方法的成像结果对比如图6所示．在方位向边缘处(目标1、15)，由于调频率空变严重，使得传统线性调频变标方法严重散焦；在距离向边缘处(目标3)，由于等效速度空变，使得传统线性调频变标方法的补余距离徙动不精确，会有轻微散焦；而笔者提出的成像算法对各目标都可实现良好的聚焦．

图6 部分点目标的传统线性调频变标方法与笔者提出方法成像结果的对比

4 结 束 语

笔者针对GEO-LEO双基地合成孔径雷达系统的成像处理，提出一种基于二维时域扰动的改进型线性调频变标成像算法．根据双基观测几何，建立了非“走-停”假设下的等效单基斜距模型．基于该模型通过二维时域扰动的方法校正回波的距离徙动空变和方位调频率空变，并对残余相位进行补偿．该算法可实现GEO-LEO双基合成孔径雷达高分辨率宽幅场景的良好聚焦，且具有很好的保相性能．仿真实验验证了该算法的有效性．这项研究成果可有效地推动我国未来GEO-LEO双基合成孔径雷达系统成像技术的发展．