集体防御机制下同质网络行动同步建模与控制

王 刚，胡 鑫，马润年，刘文斌

(1. 空军工程大学 信息与导航学院，陕西 西安 710077；2. 温州大学 计算机科学与工程学院，浙江 温州 325035)

网络同步是网络各子网、节点之间围绕同一任务/目标开展的协作行动．在网络安全集体防御机制中，网络行动的同步与控制建立在集体协作基础上，通过各子网、节点间遂行自动化和互操作的集体防御行动，抵御不确定网络攻击，将攻击后果最小化，同时提升网络态势感知、自愈修复和动态防护等能力；网络行动同步是实现集体防御的重要基础和核心环节[1]．根据要素成员性质和整体拓扑结构功能的差异，网络可进一步区分为同质网络和异质网络．同质网络是指具有相似的网络结构、特点及网络间的耦合模式的网络，其相似性越强的网络，越容易实现网络同步[2]，如作战体系中的指挥控制网络、态势感知网络和火力打击网络都是同质网络．而现实作战体系通常是多类型同质网络或网络节点的混合叠加，如指挥控制网络与态势感知网络交叉构成的态势感知和控制网络[3]，就是典型的异质网络．异质网络是指将不同网络结构、特点和网络间的耦合模式的网络，通过不同的方式逐步汇聚到同一类网络中[4]．相关研究通常建立在同质网络分析的基础上．在网络同步方面，相关研究主要集中在不同类型网络拓扑的同步建模和控制．如针对同质网络的同步与反同步的自适应控制及仿真[5]，复杂网络时滞的自适应同步分析[6]，双重时滞的动态网络同步算法设计及仿真[7]，针对异质网络的参数未知耦合时滞的广义同步与仿真分析[8]，非线性网络的主动控制与自适应控制同步及仿真[9]，复杂动态网络的时滞同步及仿真[10]，非线性耦合时滞网络的自适应同步[11]．在网络安全集体防御机制下，网络行动的同步问题出现了新的特点:网络发生随机故障和遭受攻击的复杂不确定性[12]，影响网络节点信息获取、处理和交互的能力，需要在传统同步模型的基础上增加不确定性因子，建立新的同步模型;在不确定因素的影响下，网络安全集体防御的同步控制，需要考虑网络节点/链路连接关系等网络参数的复杂多样性，根据参数信息差异，分析网络同步控制．值得注意的是，网络子网中各节点间的通信连接关系决定子网的功能和特性，进一步决定网络与网络之间的相互作用关系，从而影响网络整体的集体防御效能．因此，网络子网中节点间的同步是集体防御的关键，最基本的问题就是同质网络行动的同步问题．

笔者从网络安全集体防御的分析入手，引入不确定性因子，构建集体防御机制下同质网络的行动同步模型，并利用主动控制和自适应控制，分别分析在参数已知和未知条件下的网络行动同步控制．

1 集体防御机制下的同步建模

网络安全的集体防御行动是动态的系统运行过程，对网络初始状态的变化很敏感，网络初值的微小变化就可能影响网络安全防御行动的整体效能，同时易受外界环境的影响而偏离预期行动轨道．从局部和短期看，网络安全集体防御行动可能是无序和混乱的．从整体和长期看，应建立基于某类行动规则和行动控制规则，通过同步策略和人为控制，实现有序化和同步．在集体防御机制下，各子网节点间应相互联系、协同共享，共同构成连续、线性的动态网络，通过同步行动，实施网络的实时动态安全防御[1]．

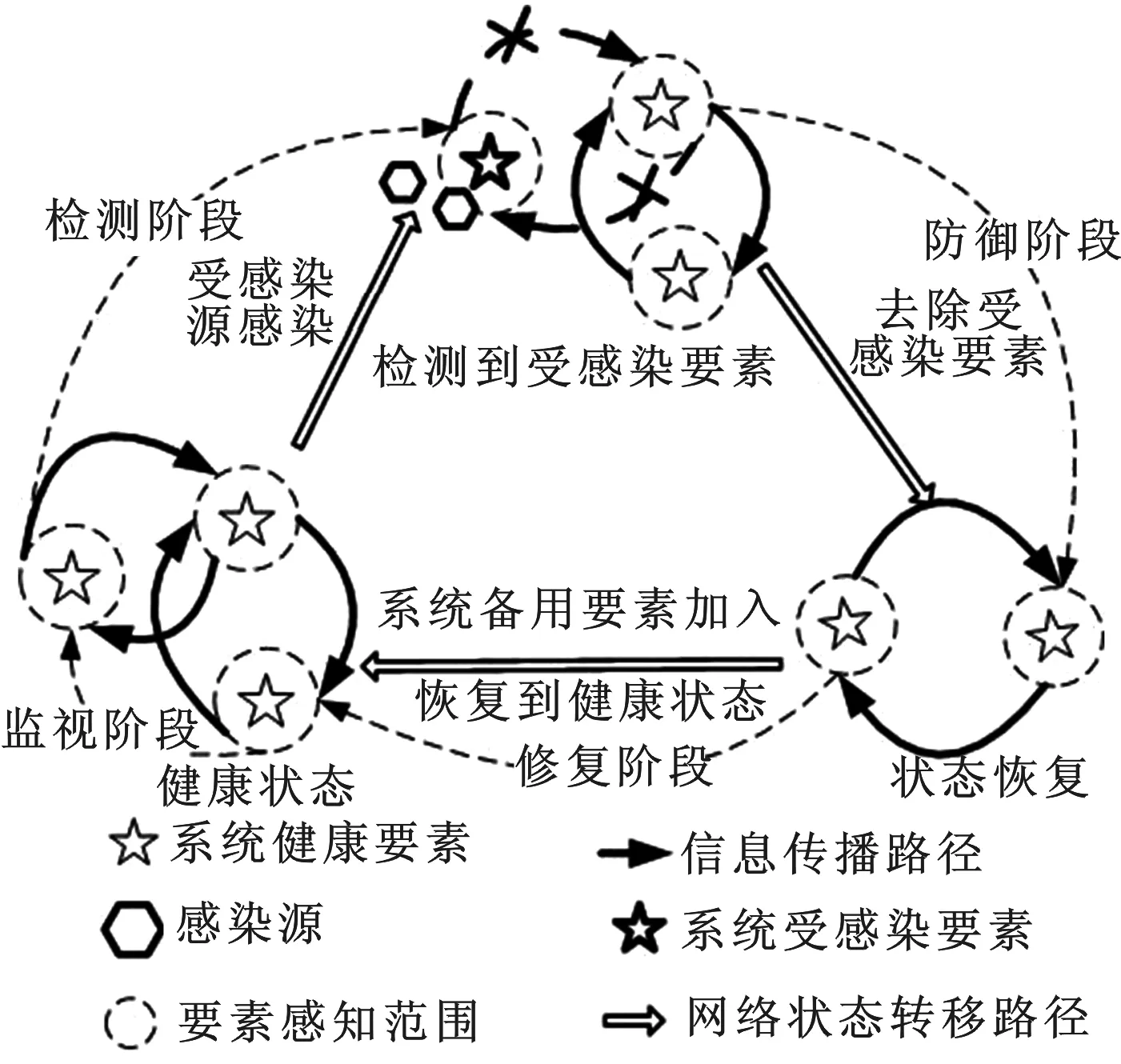
图1 网络安全的集体防御

根据网络状态差异，网络安全集体防御可划分为监视—检测—防御—修复等4个阶段[1]，如图1所示．其中影响网络行动同步的主要因素包括:网络中节点间的通信连接关系，它通过影响网络中信息的收发、处理和共享能力，影响网络安全集体防御效能和同步能力;网络行为的复杂性和不确定性，网络自身故障发生的随机性和遭受对手网络攻击的不确定性，将直接影响网络的功能、传输特性等能力，作用于集体防御效能及其同步能力．

对于同质网络行动同步问题，应考虑针对网络安全集体防御的复杂不确定性，在同质网络动力学模型的基础上，增加不确定性因子，得到集体防御机制下的同质网络行动同步模型:

(1)

(2)

根据式(1)构建相应的动态网络，则有

(3)

其中，ui(t)∈RN×N，为控制输入．当集体防御行动达到同步时，满足

(4)

其中，s(t)∈RN×N，为网络达到同步状态时节点的状态变量，此时，网络中不存在耦合控制项，即

(5)

集体防御行动达成同步的动力学模型可表示为

(6)

2 主动控制同步

将式(3)中节点i的动力学函数F(xi(t))改写为F(xi(t))=Axi+f(xi(t))[13]，其中A∈RN×N，为常数矩阵，f(xi(t))为非线性函数，则式(3)可调整为

(7)

(8)

根据式(4)，定义系统误差变量为

ei(t)=xi(t)-s(t) ， 1≤i≤N．

(9)

为此，对于式(7)所描述的同质网络，如果存在控制器ui(t)，使得式(7)在任意初始状态(x1(0)，x2(0)，…，xN(0))条件下，均满足

(10)

则动态网络趋于同步．

由式(7)和式(8)得网络误差系统，即

(12)

将式(12)代入式(11)，可得方程

(13)

在此情况下，通过调整V1使得式(13)满足Lyapunov稳定条件，令

V1=Mei,

(14)

将式(14)代入式(13)，可得

(15)

此时，选取式(14)中的矩阵M，使得矩阵P的特征值的实部均为负值[14]，保证式(15)渐近稳定于原点，即可实现式(7)和式(8)的同步．

3 自适应控制同步

在驱动系统(式(1))的基础上，构造相应的网络参考模型(即响应系统)为

(16)

为实现参考网络与原网络的同步，根据式(9)定义两个网络节点状态变量之间的误差:

(17)

根据式(1)和式(17)，可得网络误差系统为

(19)

自适应控制器可表示为ui(t)=-diei(t) ， 1≤i≤N．

(20)

并且存在非负常数ki，满足：

(21)

证明 构造Lyapunov函数:

(22)

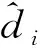
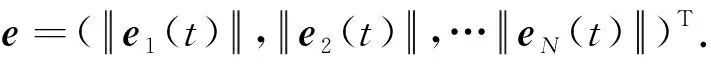
4 仿真分析

网络行动同步问题可归结为混沌系统研究范畴．在混沌系统的研究中，最为经典且运用最为广泛的是Lorenz混沌系统．Lorenz混沌系统存在如下特性[15]:初值敏感性．系统初值条件的微小变动会导致网络状态发生巨大差别，即通常所说的“蝴蝶效应”．脆弱性．由于系统的初值敏感性导致系统很容易受到外界的影响，进而影响系统整体效能．可控性．系统在初始阶段处于混乱、无序的混沌状态，但在后期可人为地调节系统的相应参数，进而实现系统的有序、同步．Lorenz混沌系统的诸多特性与网络安全的集体防御行动的基本特性在一定程度上存在一定的相似性．因此，运用Lorenz混沌系统研究网络安全的集体防御同步具有一定的合理性．

考虑网络发生随机故障和遭受攻击的复杂不确定性，减小不确定因素对网络安全集体防御行动的影响．分析Lorenz混沌系统方程结构，考虑在系统的第1个方程施加含有状态变量y和z控制信息的可变系数乘积项，通过调节可变系数有效控制不确定因素对集体防御行动的影响，其动力学方程为

(24)

选取a=10，r=28，b=8/3，初值为(x0，y0，z0)=(1，2，1)，节点总数N=50，内耦合矩阵H为单位阵，耦合系数c=1，为方便计算，选择lij= 0.1 (i≠j)，则根据式(2)得，lii= -4.9．因此，其耦合矩阵L为

(25)

分析式(24)中李雅普诺夫指数λ与可变系数h的演化关系，合理选取可变系数h值作为式(24)的参数，对应h变化的李雅普诺夫指数谱如图2所示．其中，当λ1≈0，λ2<0，λ3<0 时，系统处于周期状态；当λ1≈0，λ2≈0，λ3<0 时，系统处于二维拟周期状态；当λ1>0，λ2≈0，λ3<0 时，系统处于混沌状态．当h∈ [0，1.3]∪ [1.7，2.3]时，λ1>0，λ2≈0，λ3<0，表明系统在该区域内一直处于混沌状态．由此，分别选取可变系数h=0、h=1 和h=2，分析系统的同步误差随可变系数h的变化情况，网络发生随机故障或遭受攻击对网络安全的集体防御行动同步的影响．其中，图3表示可变系数h=0 的情况，即此时网络不存在不确定性因子，为传统的网络行动同步，而图4和图5分别表示可变系数h=1 和h=2 的情况，即此时网络存在不确定性因子的情况．显然，网络同步误差ei1、ei2和ei3均在短时间内收敛到零，系统达到同步，而对于不同的不确定性因素h，网络同步前的误差随h增大而增大，网络达到同步所需时间也越长．

图2 随h变化的李雅普诺夫指数谱图3 h=0时系统的同步误差

图4 h=1时系统的同步误差图5 h=2时系统的同步误差

仿真结果表明，当网络不受不确定性因素影响时，网络不发生随机故障或遭受攻击，网络的同步能力最强;当网络受不确定性因素影响逐渐增大时，网络发生随机故障或遭受攻击导致网络中相关节点/链路被移除，网络节点之间的连通性降低，随着发生随机故障或遭受攻击的增多，相应的集体防御机制下的网络同步能力减弱．因此，相较于传统网络行动同步，集体防御机制下的同质网络行动同步模型能够在一定程度上适应网络发生随机故障和遭受攻击的复杂不确定性，并根据特定的网络行动和任务承载，动态调整可变系数h能有效控制和减小不确定因素对网络安全的集体防御行动同步的影响．

5 结 束 语

文中针对网络安全集体防御特点，引入复杂不确定性因子，构建同质网络行动的新型同步模型；利用主动控制和自适应控制分别研究了在参数已知和未知条件下的网络行动的同步与控制；通过仿真验证了结果的有效性和可行性．