威布尔分布在面向服务的再制造回收决策中的应用

张 丹，蔡宗琰，刘清涛

（长安大学 工程机械学院，西安 710061）

0 引言

人类文明发展以来，对地球资源的消耗已经超出其恢复能力，大力发展经济的同时要遵循科学发展理念，可持续发展是我国科学发展理念之一，要求发展必须以不损害后代人利益为代价，一方面达到发展经济的目的，另一方面保护好人们赖以生存的地球。为了缓解资源消耗的速度与人类发展之间的矛盾，最大限度挖掘产品剩余价值，二十世纪九十年代，美国率先提出再制造这一概念，经过多年的发展已经具备一套完整体系。中国再制造起步较晚但发展迅速。

在传统的再制造废旧设备回收模式下，废旧品的回收都是在设备完全报废之后进行，也是目前主流回收模式。在设备完全报废后回收的废旧品，质量参差不齐，用于废旧品再制造的加工工艺也不相同，而产品服役期间，在达到预定的再制造时间点，无论设备在该时刻状态如何，都进行回收，那么用于再制造的废旧品质量得到了保证，并且制造工艺路线也变的简单。因此，定期回收再制造受到学者以及企业的关注[1]。

柯庆镝[2]、宋守许[3]等就再制造废旧设备最佳回收时期问题，提出了主动再制造理论，并分析对比了传统再制造模式与主动再制造模式的相同与不同之处，得到了适用于主动再制造理论的最佳回收时机，主要零部件优先和可成批性。利用建立服役时间冗余强因子，寿命匹配等方面在产品设计初始通过零部件层和结构层的优化降低零部件的不确定性，再通过服役时间冗余强因子，寿命匹配等确定设备回收的最佳时机。

1 面向服务的再制造

1.1 面向服务的再制造含义

全球经济飞速发展，竞争日益变得激烈，产品越来越向服务经济过度，企业也从传统的以产品为核心演变为以产品和服务为重点的新型模式，传统制造业在时代变革的驱使下也从单一的制造加工价值链向制造加工与服务的综合模式延伸，制造业与服务业越来越融合，越来越相互依存，服务的战略意义及其占企业收益比重也逐步增加。

在传统再制造模型基础上，将原来制造业处于中游的产业链扩展至上游与下游，形成一条涵盖了上、中、下的整体产业链。图1所示为文章描述的这一模型。该模式使设备在设计初始就面向再制造设计，让其更易拆卸，替换与装配，使再制造变的简单，整个价值链上游价值增加。通过回收，为客户定制全寿命周期内解决方案，优秀的售后服务可使再制造品的营销战略更加成功，实现了整个价值链下游价值增加。整个过程中，客户全程参与，可将信息，建议以及意见向企业反馈，企业与客户之间的互动使服务价值增加[4]。

图1 面向服务的再制造模型

1.2 面向服务的再制造特点

1）回收时机最佳：设备服役期间，其运行规律大致符合浴盆曲线，服役前段处于磨合期需调试，失效率较高，但此时间段内维修简单，成本低廉；磨合期结束后为设备平稳运行阶段，此阶段偶发故障多由于人工操作失误，维修较为容易；到了曲线第三阶段损耗期，该阶段维修频次与维修成本上升。因此在设备进入第三阶段且没有彻底报废之前确定回收时机，回收再制造，可将企业成本控制在最低。

2）批量回收：传统再制造回收模型在设备报废之后进行回收，由于回收渠道不同，回收行为不规范，回收的废旧设备质量各不相同，这也使后续再制造工艺路线有所差别，一系列问题导致再制造生产无法批量进行。而在面向服务的再制造模式下，设备回收在彻底报废之前，在确定最佳回收时机后，同批次设备处于正常运行状态，损坏程度近似，在此时回收，再制造工艺路线基本相同，实现了再制造批量生产[2～4]。

3）服务优先：面向服务的再制造模式为客户给与全寿命周期的解决方案，将关注点放在服务上，而不仅仅是产品自身，在客户的沟通互动过程中实现共赢[5～7]。

2 面向服务的再制造最佳时机预测

面向服务的再制造模式的其中特征之一便是时机最佳性，在什么时机进行废旧设备回收十分关键，如果回收过早，设备的原始价值没有被利用完全，回收的过晚，设备损耗严重，回收难度增加，这就违背了可批量性生产的原则，造成资源损失。因此确定最佳回收时机至关重要。

2.1 模型假设

前文中提到机电设备的服役曲线符合浴盆曲线，在设备服役前期，设备处于磨合期，需要调试，虽然故障率高，但是维修简单，成本较低；在进入浴盆曲线的第二阶段，故障率上升，此阶段的损坏多数由于人为操作不当造成，维修频率低，维修成本低，在进入浴盆曲线第三阶段，设备故障率迅速上升，此阶段由于设备长时间磨损，锈蚀，疲劳等原因，维修频率与维修成本快速上升，文章决策模型中考虑从浴盆曲线第三阶段研究[8]。

2.2 威布尔分布

威布尔是连续型分布函数模型，它广泛应用于设备和零部件的寿命预测，可靠性分析等。它先大致给定可靠度下零部件损耗开始时间Tb，但这并不是最佳回收时间，这一时间点处于浴盆曲线第三阶段，可靠度符合要求，而在这一阶段零部件出现一定程度的损耗，并经过多次维修，无法断定是否能够通过再制造使其恢复初始性能，而传统再制造模式在此时进行回收。因此回收最佳时间的确定及其重要[9]。

文章提出只考虑产品的浴盆曲线第三阶段的维修成本，另外，设备初始价值与再制造成本是设备在原始寿命周期服役的成本组合。

因此，目标设备在原始寿命周期内单位服役年限的成本最小值：

上式中：

D0为产品的原始价值；

Dr为再制造成本系数；

Dm为维修成本期望值；

M(t)为累计失效次数；

SD(tb)为优化目标；

tb为决策变量，即再制造时机，

t3为浴盆曲线的第三阶段起点。

式中：

g(s)为产品的失效概率函数，可由威布尔拟合失效数据确定[10]。

三参数威布尔分布模型在结构与参数选取上都较为困难，实践中通过优化后的两参威布尔分布模型应用较为广泛，两参威布尔分布累计失效与概率密度函数如下：

两参威布尔故障率函数：

将式(4)代入式(1)中，文章使用数值逼近方法求解目标值。

2.3 参数估计

现阶段用以拟合威布尔分布参数有几种方法，使用极大似然估计法过程繁琐，图估计法情况类似，因此这两种方法不常使用，而最小二乘法由于操作简单，精度准确等有点，文章采用该方法来拟合威布尔分布参数。

使用最小二乘法对参数进行估计时，因先估计该产品的累计失效概率，累计分布函数的准确性在一定程度上影响参数估计精确与否。经验分析法是实践中常用的累计失效概率方法：即利用经验公式从维修时间序列里计算得出各个维修时间的累计失效分布函数值。（t1，t2，…，tn)，文章使用中位秩方法预估ti时刻累计失效分布函数F(ti)的预估值：

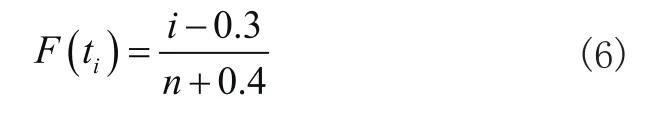
其中，i为失效顺序；n是样本值[11]。

累计失效概率预估是建立在采集来的数据样本之上，失效数据充分体现了设备以及零部件在运行过程内的寿命演化，以此作为参数预估样本比较理想。数据收集渠道主要有产品的实验结果数据和收集的现场数据，实验数据涵盖了整台设备及其零部件的数据。建立在失效数据基础上，利用中位秩法以及最小二乘法进行两参威布尔分布的数值预估，步骤如下：

两参威布尔的可靠度表达式：

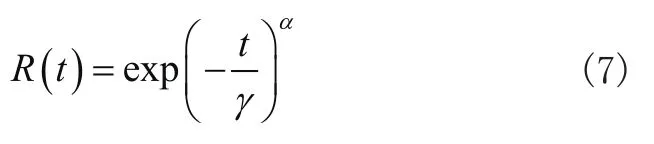
将失效率和可靠度关系式：

代入式(5)中，在对代入后的式子取对数两次之后将其简化成直线方程：

得到：

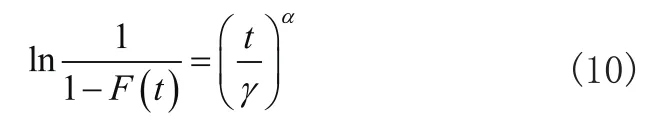
继续进行取对数操作：

将式(11)进行变形，使其成为y=ax+b的形式，最小二乘法预估参数的中心思想是令想求解的值与实际值两者间误差平方和最小，从而得出数据最优函数匹配，计算式如下：

结合式(12)，先得到威布尔分布的两个参数数值和失效分布函数，再联合式(1)和式(2)，利用MATLAB优化工具箱函数得到再制造最佳时机[12,13]。

3 实例验证

文章选取徐工XE80A型挖掘机作为研究对象。表1为验证对象失效数据。该型号挖掘机使用的发动机总成30000元，令再制造成本系数为10000元，柴油机进入浴盆曲线的第三阶段，维修成本期望为3000元，利用算例仿真分析证明文章提出的决策模型在面向服务的再制造时机预测中的应用。

依据以上数据，利用最小二乘法得到威布尔分布形状与尺度参数是7.3788，14451.7。将得到的数据带入决策模型，通过MATLAB求解，得到再制造最优时机为14782小时，以每年298天，每天运行7小时，挖掘机在7.08年后进行回收合理。

4 结论

文章针对机械设备的失效规律符合浴盆曲线，提出了一种新型的再制造模式，即面向服务的再制造模式，分析设备应在浴盆曲线进入第三阶段后开始回收工作，以设备单位时间内运行成本最小作为求解目标，利用两参数威布尔分布拟合失效函数。得到设备单位时间内成本最优的最佳回收时刻，并通过实例来验证文章所提出的模型，证明了所建立模型的可行性。

表1 实例失效数据