模糊层次分析法中权重求解的线性目标规划模型

闫利军，樵军谋，徐 坚，梁 辉

（西北机电工程研究所，咸阳 712000）

0 引言

层次分析法（Analysis Hierarchical Process,AHP）是一种有效的数学分析与评价决策工具，它将加权方法与主观测度方法结合在一起，能够较好地解决多准则决策问题。AHP具有一系列优点，它使用简单，通过建立各层因素间两两比较判断矩阵的方法来确定各因素的权重；能够将定性分析转换成定量计算，有效地将决策过程的定性因素和定量因素进行统一的量化处理，使得能够用数学方法对决策模型进行分析和运算；提供对群体决策的支持。总之，AHP具有坚实的数学理论基础，已经被用于多个领域解决多准则决策问题[1～4]。

尽管AHP方法具有诸多优点并在评价决策领域获得广泛应用，但直接将它用于产品设计方案的选择评价并不合适，这是因为AHP本身是一种确定性的决策分析工具，它基于决策者对评价目标的精确估计建立两两比较判断矩阵，从而获得评价目标之间的相对权重，这种方法并不符合实际的设计决策情形。产品开发早期的方案设计阶段具有典型的不确定性，决策者大多只能依靠定性的分析，而不是定量的计算进行方案的分析决策，因此其判断存在一定程度的模糊性，精确估计评价目标之间的相对重要性通常十分困难。因此，为了有效处理评价决策过程中的不精确判断信息，模糊层次分析法（Fuzzy AHP，FAHP）应运而生且得到了广泛的应用[5～8]，FAHP用三角模糊数或梯形模糊数表达决策者的判断，它能够有效表达决策者思维上的模糊性和不确定性，更加符合实际的设计决策情形。

FAHP应用的关键问题是如何从模糊判断矩阵中获得评价目标的权重向量。已有较多的学者对此问题进行了研究[5,9～11]，并提出了多种权重求解方法，如对数最小平方法（LLSM）、几何平均法（Geometric Mean Method）、限度分析法（Extent Analysis Method）、模糊偏序规划（Fuzzy Preference Programming）等，所有这些方法中，限度分析法由于使用简单而获得广泛的应用，但是Wang等[12]通过研究发现这种方法有时会得出错误的结果而导致决策者做出错误的决策。本文研究的目的是为FAHP寻求一种合理而简单的权重求解方法，从而克服已有方法的不足，提高FAHP的使用效率和可靠性。为此，本文以模糊判断矩阵的不一致性程度最小为目标，建立了一种模糊权重求解的线性目标规划模型。该模型使用简单且容易求解，基于该模型计算能够获得可靠的元素权重。

1 FAHP中权重求解的线性目标规划模型

对于FAHP，为了从建立的模糊判断矩阵中获得评价目标的权重向量，本文建立了一种权重求解的线性目标规划模型。下面以三角模糊数判断矩阵为例描述该模型的建立过程，建立的模型完全可以推广到区间模糊数和梯形模糊数判断矩阵的情况。

如果判断矩阵为完全一致性矩阵，则有：

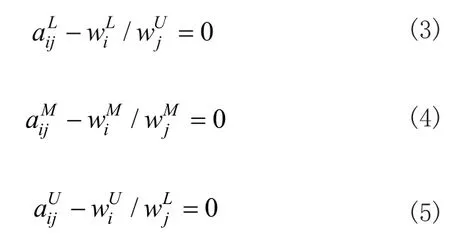
式(3)～式(5)等价于：

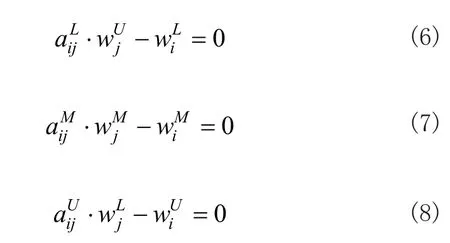
如果判断矩阵为不一致矩阵，则令：

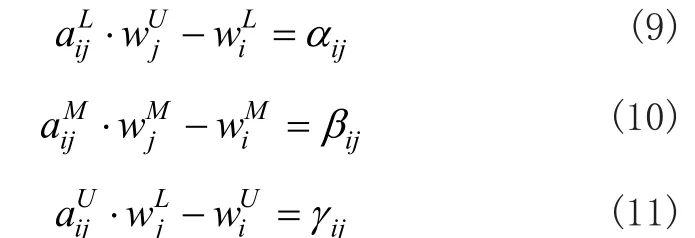
其中αij、βij、γij表示不一致性引起的估计偏差。

2）式的目标函数是要使决策者的估计和元素重要性比值的期望之间的偏差最小，其根本目的是追求判断矩阵的不一致性程度最低。因此，式(2)的目标函数等价于：

根据Wang和Elhag的研究结果[12]，模糊归一化的权重向量一定满足下列约束条件：

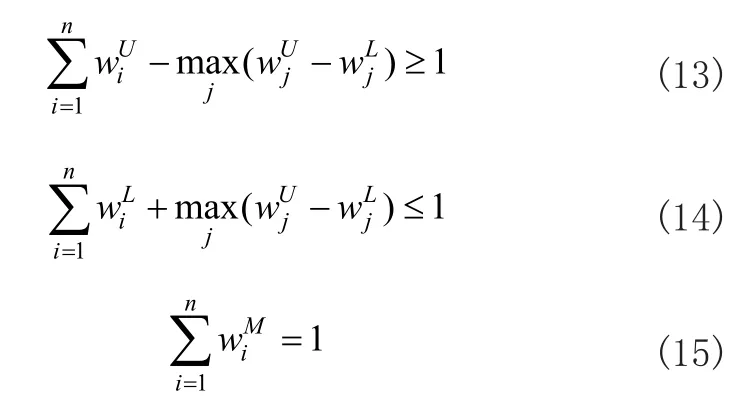
式(13)～式(15)等价于：

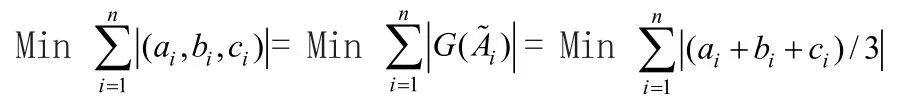
由于|(a+b+c)/3|≤|a|+|b|+|c| ，所以：

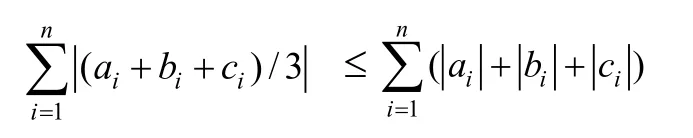
基于以上分析，本文建立的非线性规划模型为：Min：

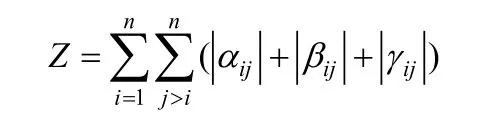
令：

i=1,2,…,n，i＜ j ＜n，则有：

从而，将式(19)的非线性规划模型变换成式(20)的线性目标规划模型：

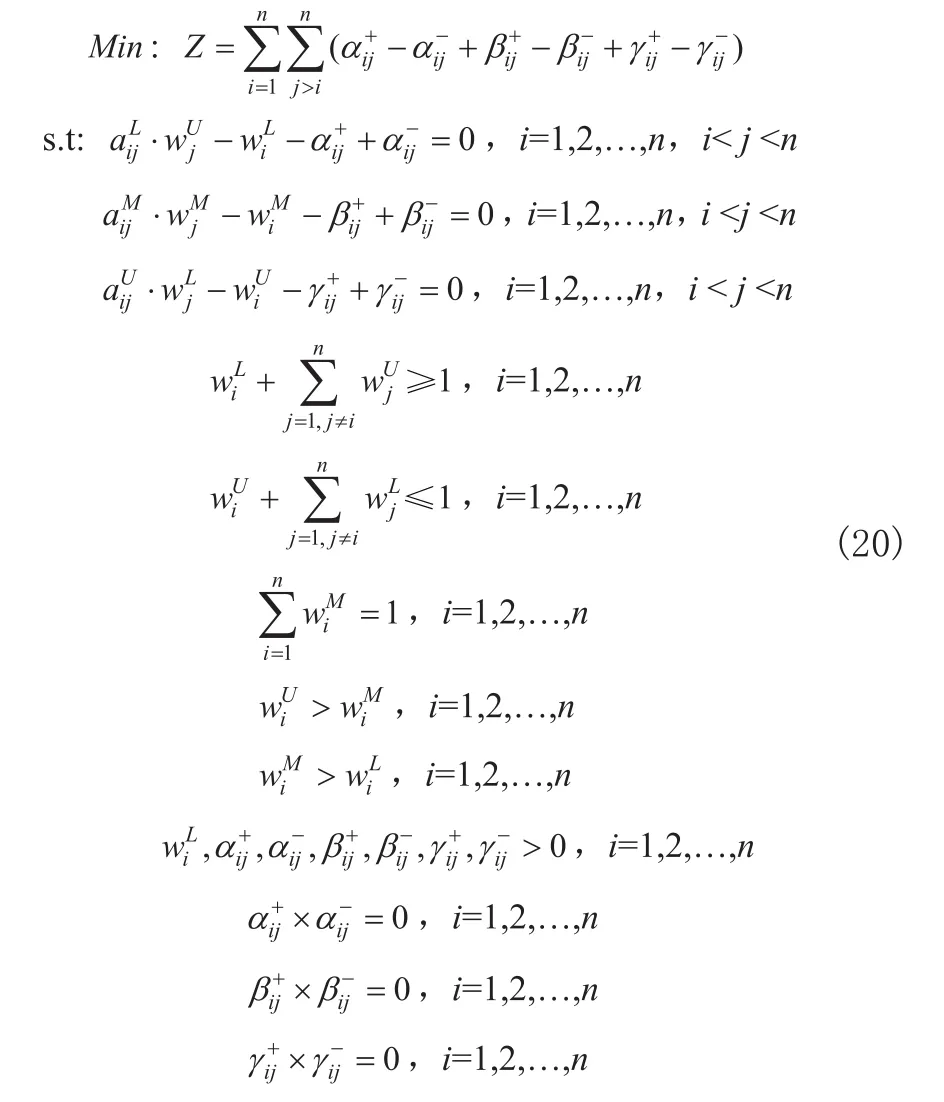
对该模型的求解，可采用单纯形法，具体过程不再详述。对任何满足一致性指标的三角模糊判断矩阵，其规划模型中的目标函数值等于0。反过来，如果规划模型中目标函数的值为0，那么就一定可以肯定相应的三角模糊矩阵为一致性判断矩阵，否则，为非一致性判断矩阵，且目标函数值的大小反映了判断矩阵的不一致性程度。

2 实例分析

对该判断矩阵，采用本文目标规划方法得到的模糊归一权重为：

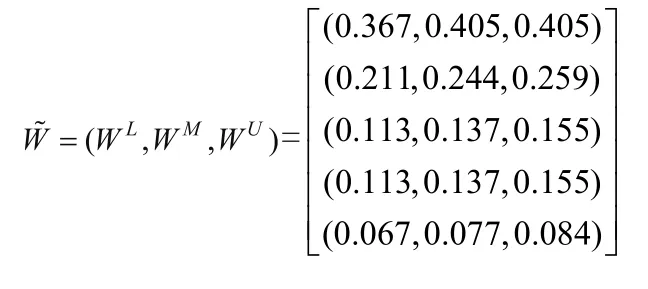
该权重向量对应的目标函数值为：Z*=0.034。由于目标函数值不等于零，因此可以肯定该矩阵为不一致判断矩阵。

对此判断矩阵，文献[15]采用限度分析法得到的确定性权重值为W=（0.46，019，0.12，0.12，0.11）T。可以发现，该结果的前三个元素权重0.46，0.19和0.11均超出了它们的合理取值区间（（0.367～0.405），（0.211～0.259），（0.113～0.155））。因此，其结果是不合理的。Wang等[12]研究认为通过限度分析法获得的权重并不能真正反映决策准则或备选方案之间的相对重要性，因此，也不能作为这些元素的重要性权重。这就是为什么在上述实例中采用限度分析法得到的确定权重值超出了采用目标规划方法得到的模糊权重的区间范围的原因。

3 结论

考虑到模糊层次分析法在实际的评价决策领域应用的广泛性，以及通过模糊判断矩阵求解元素权重的困难性，本文以模糊判断矩阵的不一致性程度最小为目标，建立了一种模糊权重求解的线性目标规划模型，在权重的合理范围内寻找使目标函数最优的期望权重作为最终的评价元素权重，目的是使得元素重要性权重与决策者估计之间的偏差最小。通过实例计算并和文献中采用限度分析法给出的结果进行比较，指出限度分析法计算得到的元素权重的不合理性。