LCLC补偿型电场耦合式无线电能传输系统特性分析

余江华，孙岩洲，张笑林，韦延方

（河南理工大学 电气工程与自动化学院，焦作 454000）

0 引言

无线电能传输（Wireless Power Transfer，WPT）技术是指不通过直接的电气连接将电能从电源侧传输到负载侧的一种新型电能传输方式，可使用电设备摆脱传统的线缆束缚，在一些特殊的场合有着美好的应用前景[1]。基于电场耦合式电能传输（Electrical-field coupled power transfer，ECPT）技术作为无线电能传输技术之一，采用金属薄板作为发射电极和拾取电极，通过极板间建立的高频电场作为载能介质，实现电能的无线传输，具有电磁干扰性小，耦合机构灵活性高的特点[2～5]。目前该技术已在植入式医疗器械和电动汽车等近距离传输场合得到应用[6,7]。由于ECPT系统中耦合机构的等效耦合电容值较小，耦合容抗大，需要对系统的耦合机构进行谐振补偿[8]，目前ECPT技术多采用LC串联谐振补偿网络[9]，采用该种补偿方式存在补偿电感体积过大以及系统对谐振频率的鲁棒性较差等问题。

文献[10,11]将LCLC补偿网络运用到ECPT系统中，在有效解决上述问题的同时也使ECPT系统的传输功率和效率产生了质的飞跃[12]。经研究发现，由于该补偿网络阶数较高，参数变化时对系统输出功率和效率有着较大的影响，然而对于一个ECPT系统来说，相关参数特别是耦合电容、负载和谐振频率等具有较大的变化特性。为了得到双边LCLC对称补偿型ECPT系统中易变参数对系统输出特性的影响规律。本文通过电路理论建立LCLC对称补偿型ECPT系统的等效电路模型，分析了耦合机构的等效电容、旁路并联电容、负载和频率变化时对系统输出功率和效率的影响规律，所得结果可为LCLC对称谐振型ECPT系统的设计和调试提供参考。

1 系统建模

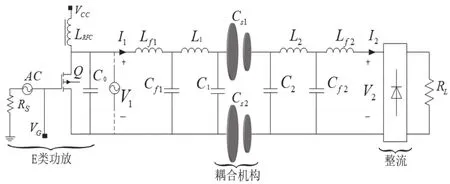
图1 系统等效拓扑电路图

所设计的完整ECPT系统电路如图1所示，采用E类功率放大器作为系统的高频电源；耦合机构作为ECPT系统的核心部件，由两对铜制薄板构成；为减小系统的谐振补偿电感量，发射极板侧和接收极板侧并联旁路电容C1和C2；由于本文主要分析LCLC对称谐振型补偿网络，为简化分析电路，将E类功放等效为输入电压源V1，负载侧获取电压等效为V2；耦合机构等效为集总电容CS1和CS2。

在理想情况下耦合机构等效集总电容CS1和CS2的表达式为：

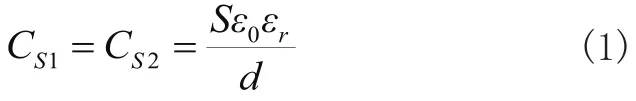
式中S为耦合极板有效耦合面积，d为耦合间距，（8.85×10-12）为真空介电常数，为所选电介质的相对介电常数。

系统两边采用对称式结构设计，对应位置上元器件参数取值相等，即Lf1=Lf2、Cf1=Cf2、L1=L2、C1=C2；等效耦合电容CS1、CS2串联成总耦合电容CS，CS与C2串联后再与C1相并联为电容Ch；Lf1和Cf1在角频率ω下发生谐振；L1与Ch发生谐振的同时也要与Cf1发生谐振；各元器件相互关系表达式[10,11]为：

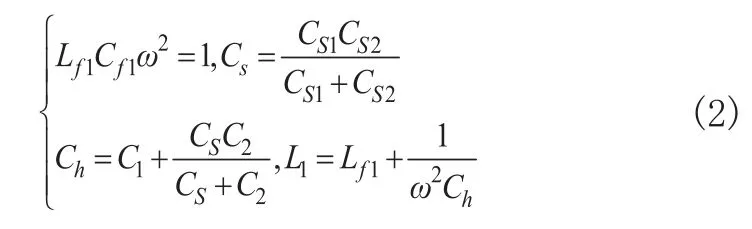
等效电源V1与I2关系表达式，等效负载电压V2与I1的关系表达式以及输出功率的表达式为：

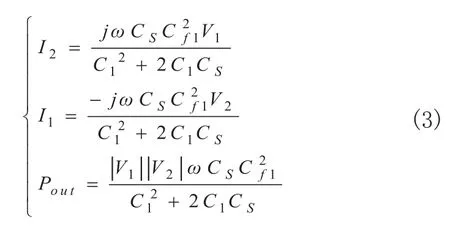
根据电路理论可知±j可以看成旋转因子，即输出电流I2超前输入电压V190度，输入电流I1滞后输出电压V290度，输入侧电压电流同相位，输出侧电压电流同相位，且与负载性质无关。

由于系统的补偿网络阶数较高，为进一步简化分析电路，应用电路星三角联结等效变换理论将图1转化为图2所示的等效电路图。

图2 星三角变换等效电路

系统采用对称式设计，对应位置上元件参数取值相等，经过星三角理论变换后对应位置上等效阻抗依然相等，即Z1=Z5、Z2=Z4，等效阻抗表达式为：

式中a=Lf1+L1-ω2Lf1L1Cf1。

各级等效阻抗表达式Zd1、Zd2、Zd3的表达式为：

采用阻抗变换原理建立等效电路图2的电压增益模型为：

将式(4)、式(5)代入式(6)可得关于参数Z1、Z2、Z3、Ze、ω、CS的电压增益表达：

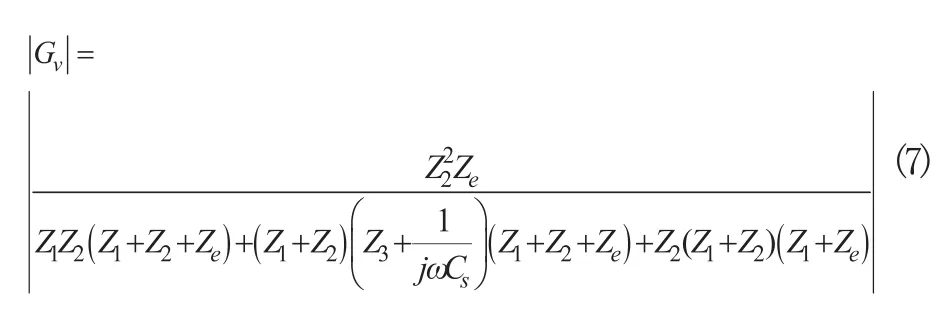
图2中系统输入阻抗Zin的表达式为：

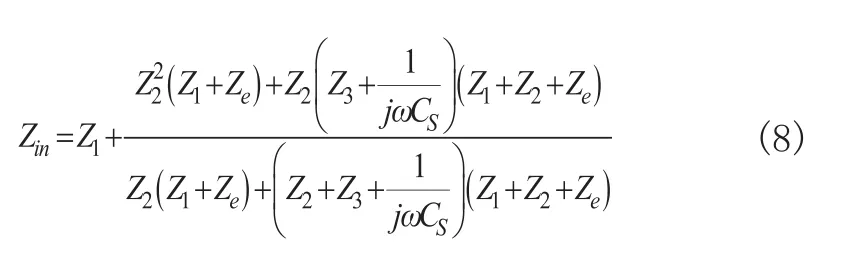
系统输出功率和效率的表达式为：

式中|Gv|和Zin取值如(7)、式(8)所示。

2 系统传输特性分析

本文设计的系统模型传输功率30W，负载50Ω，电源和负载侧电压幅值均取值55V，耦合机构等效电容200pF，旁路并联电容设定为500pF，系统频率设定为13.56MHz。通过式(2)和式(3)可计算系统其他元件参数，具体参数取值如表1所示。

表1 系统参数及元件值

以表1参数为基础，通过MATLAB仿真分析系统的频率f、等效耦合电容CS、旁路电容C1和负载Ze变化时对系统输出功率Pout和效率η的影响规律。

2.1 输出功率、效率随频率的变化规律

其他参数为设计值时，改变系统的频率，得到系统输出功率和效率随频率的变化规律如图3所示。

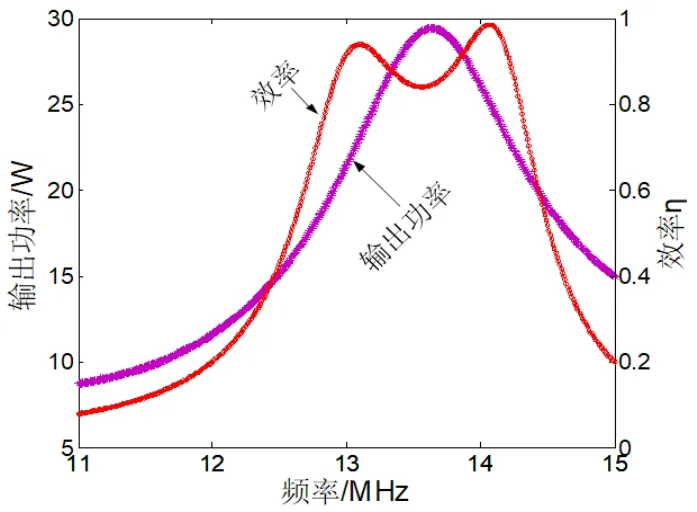
图3 输出功率、效率随频率的变化规律

由图3可知输出功率随着频率的增大先增大后减小，在谐振点达到最大值，频率的减小相对于频率的增加对输出功率的影响更为显著；系统效率在谐振频率点的两侧取得最大值，LCLC对称补偿型ECPT系统存在频率分裂现象，在调试过程中，可适当的增加或降低系统频率，以获取最优的系统传输效率。

2.2 输出功率、效率随等效耦合电容和旁路并联电容的变化规律

在实际应用中，ECPT系统的耦合极板很难保证精确对位，相对位置易发生变化，使两对耦合极板之间发生交叉耦合，在引起耦合机构等效电容变化的同时，也会造成旁路并联电容值发生改变。

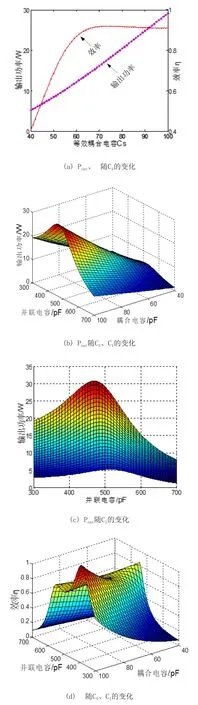
图4 Pout、η随C1、CS的变化规律

由图4(a)可知随着耦合机构的等效电容减小系统输出功率减小。系统效率在等效耦合电容值减小到设计值的60%时才开始大幅下降，即系统效率对等效耦合电容的变化具有较高的鲁棒性；由图4(b)可知当等效耦合电容值降低时，交叉耦合引起的旁路并联电容增大会进一步降低系统的输出功率；通过视角改变法可由图4(b)得到图4(c)，由图4(c)可知当旁路并联电容减小时，系统输出功率先增大后减小且可取到最大值；由图4(d)可知系统的旁路并联电容大于或小于设计值时，系统效率均先增大后再减小且都可取得最大值；综合图4(c)和图4(d)可知，当旁路并联电容减小时，系统的输出功率和效率都可取得最大值，即在系统的设计和调试过程中可在理论值的基础上适当的减小旁路并联电容的值，不仅有利于减小交叉耦合带来的影响，也可使系统的输出功率和效率均达到最优。

2.3 输出功率、效率随负载的变化规律

其他参取值为系统的设计值，系统的负载Ze分别取值为R，RL，RC。图5示出三种负载变化时对系统输出功率和效率的影响规律。

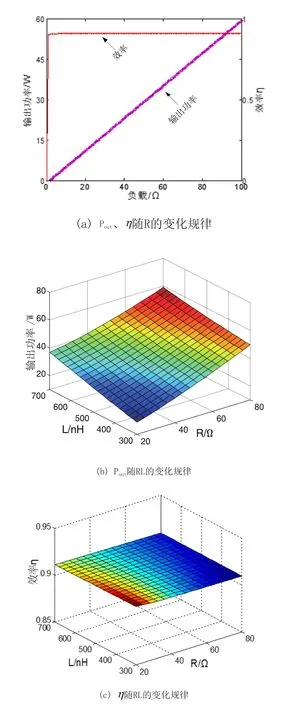
图5 输出功率和效率随负载的变化规律

由图5(a)、图5(b)和图5(d)可知系统的负载呈阻性、感性或容性时，系统的输出功率均随着负载的等效阻抗增大而增大；由图5(a)、图5(c)和图5(e)可知系统的输出效率不随负载的变化而变化，系统对负载的变化具有较高的稳定性。

3 实验

为验证上述系统的输出特性，搭建如图6(a)所示的实验电路，并省略整流模块。采用高频高效的E类功率放大器为系统提供高频电能，能够实现输出功率30W，带宽2MHz；采用4块半径为49mm的铜板作为耦合极板，可获得最大耦合电容200pF。实验参数在系统设计参数（表1）的基础上根据分析所得的输出功率最优原则选择频率13.56MHz，等效耦合电容为200pF，旁路并联电容C1(C2)为450pF，负载为50Ω，测得在输出功率最优原则下负载侧的电压幅值为50.4V，如图6(b)所示。

因实验条件有限，通过测量负载侧获取的电压幅值估算输出功率的变化趋势。当负载分别取值25Ω、50Ω和75Ω时测得负载侧电压幅值随频率和等效耦合电容的变化规律如图7所示，由图7(a)可知随着频率的增大，系统取3种负载时输出电压幅值均先增大后减小，基本都在谐振频率点达到最大输出电压。在同一频率下，负载等效阻抗越大，输出电压幅值越高。由图7(b)可知，在三种负载下系统的输出电压幅值随着等效耦合电容量的减小而减小，与图4仿真获得的变化趋势基本一致。

图6 ECPT实验电路及最佳参数时电压波形

图7 VL随频率和等效耦合电容的变化规律

4 结束语

针对双边LCLC对称补偿型ECPT系统的输出特性易受影响，而在实际应用中耦合机构的等效电容、旁路电容、负载和频率等参数又易发生变化的问题。通过电路理论建立系统的等效电路模型，采用MATLAB仿真分析系统的传输功率和效率与系统的等效串联电容、旁路并联电容、负载和系统频率的变化规律。结果表明，由于存在频率分裂现象，系统在设计谐振频率值的两侧达到最优输出效率。当等效耦合电容的变化范围小于系统设计值的40%时，系统可保持较高的输出效率。旁路并联电容小于设计值时，不仅有利于减小交叉耦合带来的影响，也可使系统的输出功率和效率均达到最优。系统的输出功率随负载的等效阻抗增加而增加，系统效率不随负载变化而变化。在LCLC对称补偿型ECPT系统的设计和调试过程中可综合调整系统频率、耦合电容、并联电容、负载使系统的输出功率和效率取得最佳。