关注学生差异 突破教学难点 打造高效课堂

范惠珍

(福建省石狮市石光中学 362700)

众所周知学生之间数学学习能力是有差异的，高效的数学课堂要求提供给学生良好的数学学习环境，使得存在差异的各类学生都可以建构起与自己能力相称的新的数学认知结构，得到全新的情感体验，进而形成良好的个性品质，达到知识与能力双赢的结果.下面结合具体案例谈谈如何关注学生学习差异，善用一些方法手段，突破教学难点，进而提升课堂教学效率.

一、善用问题变式，突破教学难点

数学是灵活的，一个知识点往往可以构造出许多道看似完全不同的题目.所谓“难题”往往源自一些基本题(母题)，命题老师通过把已知量和求解量互换、将已知条件恒等变换等手段就可以将母题改造成各种面目全非 的试题.教师讲解题目时若能找出母题，让学生参与到变题中去，难题往往就能迎刃而解.

例如数列中已知形如an=kan-1+b这样的递推关系求通项公式这一题型时，若将解决方案“用待定系数法将其转化为公比为k的等比数列，再求an”直接告知学生，许多学生难以理解.为了突破这个难点，我设计了以下题组：

已知数列{an}中，a1=2，

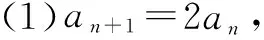
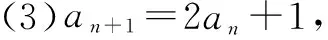
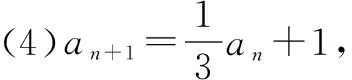
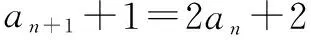
这样的“变题”使得空降的解法得以落地，使得大多数同学能更加自然地掌握这种解法.对于优生来说，或许并不需要这样的铺垫就能理解该解法，但是这样的分析有助于他们领会命题老师是如何出题的，“知己知彼，百战不殆”，这样有助于提高他们的知识迁移能力.

二、善用类比推理，突破教学难点

类比是指由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也具有相似特征的推理.通过类比，我们可以借助已经解决的问题和已经掌握的知识，理解新的知识或找到新的问题的解决办法或得出新的结论.

例如：为了让学生学会用“体积法”求三棱锥的内切球的半径，我先复习了用“面积法”求三角形的内切圆的半径.

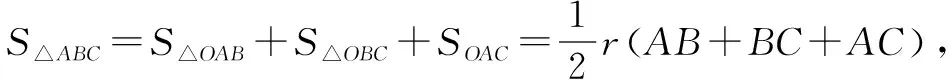
这时，学习能力较高的同学就能较快联想到用“体积法”求三棱锥的内切球的半径.

设内切球的半径为R，球心到三棱锥各面的距离恰为半径R.以球心为顶点，以三棱锥各面为底面，可以将原三棱锥分割成四个小三棱锥.

因为VA-BCD=VO-ABC+VO-ABD+VO-ACD+VO-BCD,

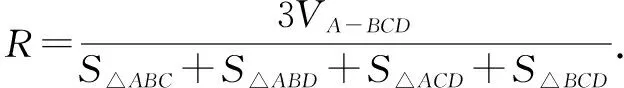
类比旧知识学习新知识，不仅有助于中等生和学困生对新知识的理解，还有助于学生对新旧知识整合，形成更加完善、更加合理的知识体系.类比有助于提高学生的知识迁移能力和创新能力，教师应重视培养学生的“类比”意识.

三、善用方法变换，突破教学难点

善用方法变换，也是突破教学难点的重要手段.换元法是解决难题、复杂问题时最常用到的一种解题方法.事实上，教师在命题时借助“换元”能够实现把不同的知识点融合到一道题中，从而把问题复杂化.

例如教师要命一道题同时考察一元二次不等式和指数函数，可以令不等式t2+t-2≥0中的t=2x，则可得到较难的不等式4x+2x-2≥0.与之相反，学生解题时，通过换元，则能化陌生为熟悉、化复杂为简单，这样的解题过程与教师的命题过程是相逆的.教师要注重培养学生的“换元”意识，无论对于哪个层次的学生，这都是他们解决陌生问题、复杂问题的有效手段.

突破教学难点，探求高效的课堂不是要消除差异，却能够帮助学困生树立学习的信心，而他们的内在积极性一旦被激发出来，则有机会进步甚至赶上，也能够在一定程度上促进中等生进步同时避免中等生沦为学困生，尤其是教师用于突破难点的策略能够潜移默化地影响优生的思维品质，进而提升整个课堂的效益.