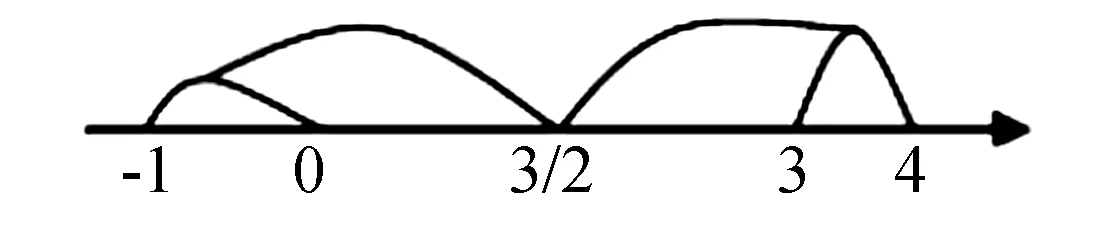浅谈高中数学“一题多解”的学习心得

王子今

(河南省实验中学高二7班 450000)

我们在高中阶段的学习，需要多加练习，尤其是数学学科，其难度提升的幅度较大，所以在解题的过程中，要及时找出自己没有掌握的知识点，查缺补漏，并总结解题的规律和经验.

一、高中数学解题过程遇到的主要困难

1.基础知识掌握不扎实

在高中数学的学习中，对于数学的练习可以巩固基础知识，并且查看自己对数学知识的学习情况，以便能够更好地进行之后阶段的学习.在解决数学练习题的过程中，我发现基础知识的掌握是解决数学问题的关键点，但是在不断学习知识的过程中，很多知识会由于时间太久被遗忘，所以会出现知识点掌握不牢固的情况.如果没有扎实的基础知识，会严重影响解题的效果，特别是在分析问题的过程中，基础知识不扎实不但会影响解题的效果，降低准确性，还会影响解题的正确性.因此，在学习的过程中，要注意对以往知识的复习，巩固自己的薄弱之处，定期对知识点进行总结和归纳，并在老师的指导下，逐步对知识点进行提升.

2.不会应用知识点

数学知识之间存在较大的关联，在计算几何题目以及代数等题目的过程中，会应用到大量的知识点，如在解决平面向量以及复数的问题中，需要应用三角函数的知识点.在解题时，熟练应用数学知识点，是解题问题的关键，但熟练应用可以将解题的效率提升，并保障解题的正确性.数学知识与知识之间并没有较多的衔接，很多知识点都需要单独学习.所以，在解题的过程中，经常会出现这样的情况，很多知识并不能熟练应用在解题当中，制约了学习的效果.

二、高中数学“一题多解”的学习心得

1.一题多解在等差数列当中的应用

例如：已知Sn是等比数列的前n想项和，S3,S9,S6成等差数列，求证：a2,a5,a8成等差数列.

在解决问题的过程中，要明确题目的考点为等差数列的定义及性质，等比数列的前n项等相关知识点的理解.其中，要找出能够应用的知识如函数与方程知识，并应用首项与公差知识进行解决.此外，在解题的过程中，还要学会应用多种思维一题多解.

在完成解题之后，还要总结解题的过程和解题的思路，如针对这道题，要学会运用函数与方程思想解题，其中首项与公比是解决等比数列问题的关键，并且应用的知识点为等比数列的通项公式、前n项和公式涉及五个量：a1，q，n，an，Sn，知道其中任意三个就可以列方程组求出另外两个.

2.一题多解在不等式当中的应用

例如：解不等式3<|2x-3|<5.

在这道问题当中，考察的知识点为一元一次不等式组的解法等，所以要应用相关的知识点，进行解答.

解法一根据绝对值的定义，进行分类讨论求解.

(1)当2x-3≥0时，不等式可化为3<2x-3<5⟹3

(2)当2x-3<0时，不等式可化为3<-2x+3<5⟹-1

所以，最终的解集为{x∣3

解法二转化为不等式组求解，原不等式等价于∣2x-3∣>3且∣2x-3∣<5⟹3

解法三应用等价命题法，原不等式等价于 3<2x-3<5或者-5<2x-3<-3，解得3

解法四利用绝对值的几何意义，原不等式可化为3/2<∣x-3/2∣<5/2，不等式的几何意义是数轴上的点x到3/2的距离大于3/2，并且小于5/2，由图象一可以得出解集为{x∣3

在解题的过程中，要应用不同的方式和方法.不等式为高中数学必须掌握的知识，所以要对解题思路进行总结，如首先需要分别求出不等式组中各个不等式的解集；其次，将这些不等式的解集在同一个数轴上表示出来，找出它们的公共部分；最后，根据找出的公共部分写出不等式组的解集，若没有公共部分，说明不等式组无解.

总之，我们在高中阶段的学习过程中，对于数学的学习需要掌握扎实的基础知识，并学会应用不同的思路一题多解.在完成解题之后，要做好总结工作，明确典型题的规律，对学习效果的提升能够起到重要的帮助作用.