理解函数单调性概念 提高学生核心素养
2018-10-10严小红
严小红
(陕西省商洛中学 726000)
一、单调性定义
1.北师大版教材中的定义
一般地对于函数y=f(x)的定义域内的一个子集A,如果对于任意两数x1,x2∈A,当x1 类似地,在函数y=f(x)定义域内的一个子集A上,如果对于任意两数x1,x2∈A,当x1 如果函数y=f(x)在定义域的某个子集A上是增加的或减少的,那么就称函数y=f(x)在这个子集上具有单调性. (1)符号语言:任意x1,x2∈A,x1 (2)图象语言:观察函数y=f(x)的图象,从左向右看,上升的为单调递增,下降的为单调递减. (3)定义的双向性:增函数:x1 y=f(x)在A上单调递减 函数单调性是一个局部概念,是针对区间而言,是区间上性质,对于单独点讨论单调性毫无意义,因此写单调区间时,区间端点可带可不带,若一个函数有几个单调递增(或递减)区间时,不能并起来,只能分开写,如单调递增区间[1,2]和[3,4],不能写成[1,2]∪[3,4],为什么这样,我们从本源问起,为什么要引入单调区间概念?只不过是为了方便函数值比较大小而已,要比较大小,只能放在一个单调区间,而在多个区间是无法比较函数值大小.同时由此还可以看出求函数单调区间,是寻求区间的最大化.如单调递增区间为[1,3],你不能写成[1,2]和[2,3]. 例1 若函数f(x)=x2+2(1-2a)x+6在(-∞,-1)上为减函数,求a的取值范围. 解f(x)=[x+(1-2a)]2+6-(1-a)2,对称轴方程为x=2a-1,则f(x)单调递减区间为(-∞,2a-1),而f(x)在(-∞,-1)为减函数,∴(-∞,-1) ⊆(-∞,2a-1),∴-1≤2a-1,∴a≥0. 例2 若函数f(x)=x2+2(1-2a)x+6的单调区间为(-∞,-1),求a的值. 解f(x)对称轴方程为x=2a-1,则f(x)单调区间为(-∞,2a-1),即为(-∞,-1),∴ 2a-1=-1,∴a=0. 这两个问题是不同的,第一个问题说明函数的单调性,即所给区间为单调区间的子区间,第二个问题是求单调区间问题,要注意分清. 证明函数的单调性只能用两种方法:①定义法(高一学生用),对于抽象函数的单调性一般用定义法证明;②导数法(相对于定义证明是比较先进的方法).判断函数单调性或单调区间的确定,可以有多种方法:①定义法;②导数法;③性质法(利用已知函数的单调性转化为函数和差的单调性或利用复合函数的单调性)④图象法(画函数图象从图中看). 例3 讨论f(x)=lnx+ax2+(2a+1)x的单调性. 解析f(x)的定义域为(0,+∞). 例4 已知奇函数f(x)的定义域为[-2,2],若f(x)在[0,2]上是递减,且f(1-m) 解析∵f(x)是定义在[-2,2]上的奇函数,且f(x)在[0,2]上是减函数, ∴f(x)在[-2,0] 也是减函数, ∴f(x)在[-2,2] 上单调递减. 只有对函数单调性的内涵和外延有深入的理解,易混的问题进行有效辨析,常见问题做到胸中有数,才能在解决函数单调性问题时,做到游刃有余,面对高考中的函数问题轻松拿下.2.对定义的理解
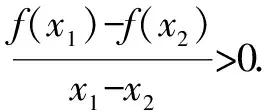

3.对单调区间理解
二、常见函数单调性问题
1.单调性证明、判断及单调区间的确定
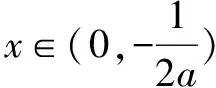
2.解抽象不等式
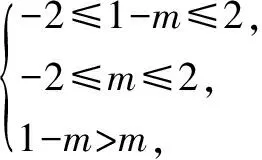

3.利用函数单调性求参数取值范围



