涉及“任意”和“存在”问题的解析与思考

汪 俊

(江苏省梅村高级中学 214112)

一、在“一题多解”，“一题多变”的方法比较中，充分理解“任意”和“存在”问题

例1 (1)∀x不等式x2+ax+1≥0恒成立，求a的取值范围.

(2)∃x不等式x2+ax+1≤0成立，求a的取值范围.

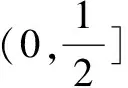
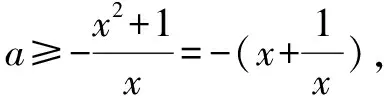
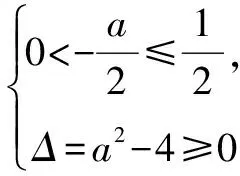
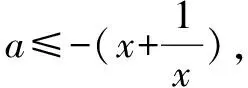
小结“任意”与“恒成立”结合的比较紧密，必须对整个区间的每个值都应该涉及.“存在”就是只需要找到一个数即可，不需要区间里每个值参与.

二、“任意”问题中的“反客为主”思想

例2 若不等式x2+px+1>p+2x对于实数|p|≤2恒成立，求x的取值范围.

分析在不等式里出现了两个字母x及p，关键在于该把哪个字母看成是一个变量，另一个作为参数，本题将p视作自变量比较简便，这样可将上述问题转化为在[-2,2]上关于p的一次函数大于0恒成立的问题.

简解将不等式x2+px+1>p+2x，变形为(x-1)p+x2-2x+1>0.

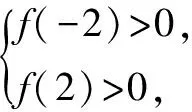
解得x<-1或x>3.

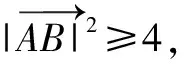
化为关于t的一次函数，可解得λ≥3或λ≤-3.

评注分清楚“主元”问题，才能有效地处理问题，必要的时候“反客为主”的方法可以更简洁有效.

三、“任意”问题中的“投石问路”策略

例3 设函数f(x)=ax3-3x+1(x∈R)，若对于任意x∈[-1,1]，都有f(x)≥0成立，求实数a的值.

分析本题是关于多次函数的不等式恒成立问题，无论是单纯求导还是分离系数都需要对a进行分类讨论，分类多，过程繁，但是如果多考虑“对于任意x∈[-1,1]，都有f(x)≥0成立”这一关键句，我们就会考虑在x=-1,x=1也成立，这样a的范围变小了，这样的“投石问路”就可以不需要对a分类讨论了.

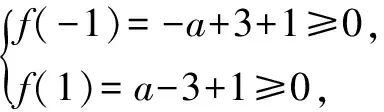
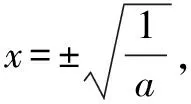
评注对参数的讨论是一个难点，一方面我们害怕分类不完全，一方面害怕分类太繁琐.所以涉及任意的问题，我们可以取特殊的值“投石问路”，让范围缩小，复杂的问题就迎刃而解了，从这个角度说，“任意”的利用价值很高.

四、任意和存在的综合性问题

例4f(x)=x2-x-1,g(x)=x3-x2-5x+m，(1)∀x∈[-2,2]，都有y=f(x)的图象在y=g(x)的图象下方，求m的取值范围.

(2)若∃a,b,c∈[-2,2]，使得g(a)+g(b)

(3)∀x1,x2∈[-2,2]，都有f(x1)≤g(x2)成立，求m的取值范围.

(4)对于∀x1∈[-2,2]，∃x2∈[-2,2]，有f(x1)≤g(x2)成立，求m的取值范围.

(5)∀x1,x2∈[-2,2]，都有|g(x1)-g(x2)|<|x1-x2|成立，求m的取值范围.

分析首先，对两个函数在区间[-2,2]的单调性，极值和最值进行研究，不加叙述.

问题(1)可以转化为g(x)>f(x)，产生一个新函数g(x)-f(x)，通过它的单调性研究，解不等式g(x)-f(x)>0；

问题(2)可以打比方：班级中存在三个同学，两个同学的体重之和小于第三个同学，这样就应该考察班级中最轻的两个小于最重的那个同学.所以问题转化为：2g(x)min

问题(3)比较常见，可以转化为f(x)max≤g(x)min.

问题(4)因为是∀x1∈[-2,2]，f(x)是小于等于所以应该考察f(x)max，而g(x)是存在，所以问题转化为f(x1)max≤g(x2)max.

问题(5)中首先的关键是处理绝对值问题，为了说明任意性，所以可以令x1g(x2)-x2和g(x1)+x1

评注涉及这类问题的题目比较多，在一个题目的背景下变式生成，对“特定句式”进行研讨，重点是需要理解和揣摩，提炼和转化出问题的关键.

总之，我们处理问题时，善于与平时的热点知识比如恒成立问题产生联系，拥有“主元”意识，必要时通过隐含条件缩小参数范围，充分借助“特定句式”进行转化，这样涉及“任意”和“存在”的问题就能够得到有效的解决.