高中数学中恒成立问题的求解策略

黄海兰

(广西省南宁市第二十九中学 530022)

高中数学中的恒成立问题大多以不等式的形式出现，而不等式两边的条件往往是解题的关键，对这些条件进行合理地变形、整理，便能让解题变得高效率、高准确率，那么又有哪些方法可以用来帮助我们整理题目中的条件进而解决问题呢？以下着重分析恒成立问题中三种常用的解题方法.

一、参变分离

恒成立问题的中档题里一般会出现一个变量，一个参数让学生计算参数范围.学生遇到此类问题时往往没有突破的方向，此时应该观察参数和变量的关系，当参数和变量易于分离，且分离后方便构建新函数时，应使用参变分离的方法做题.

例1f(x)=(x+1)lnx-a(x-1)，若当x∈(2,+∞)时，f(x)>0恒成立，求a的取值范围.

点拨因为同时考虑参数和变量的难度过高，而参变分离的使用很好地梳理了题目所给的条件，将本题转化为一道函数极值问题，进而快速解题.所以在遇到同时存在变量和未知参数的题目时不妨多使用参变分离的方法，让问题简易化.

二、数形结合

某些双变量问题中，如果直接参变分离，构建新函数，再求解，计算量会比较大，此时就需要使用另一种方法——数形结合.数形结合往往可以通过图形达到避繁就简的目的，所以，掌握这一解题技巧同样是必不可少的.

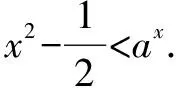
点拨数形结合往往可以将抽象的问题形象化，在解决很多类型问题时都不失为一个好方法，此处的应用也是使得大小的比较更加的直观，让解题更加容易.

三、变换主元

在恒成立问题中还有一类题目，出题者给出参数的范围，而让学生求解变量的范围.前两种在这类题型中就起不到太大的作用了，此时就需要使用变换主元的方法来解题.其实变换主元就是一种换位思考，将参数想象成变量，将变量看成参数来求解.

例3 若不等式2x-1>m(x2-1)，对满足-2≤m≤2所有的m都成立，求x的取值范围.

点拨变换主元实则就是逆向思维的过程，出题者将题目中的交换了条件和问题的位置，而变换主元就是在解题时将两者再次调换，是一种很巧妙的方法.这一方法的掌握可以开拓学生的视野，发散解题思维.

综上来看，不难发现，恒成立问题的求解，大多与函数分不开关系，不等式的外形只是为我们的求值指引方向.希望学生们掌握恒成立问题的各种解题技巧，在遇到各种恒成立问题时，可以快速拿出最有利于这道题的解题方法，降低解题的难度，大大缩短解题的时间，提高解题的准确率.