三次函数的命题相关思考
2018-10-10张秋鸿
张秋鸿
(福建省龙岩市漳平二中 364400)
对最一般的三次函数y=ax3+bx2+cx+d(a≠0)一类的问题,从解题的角度来看,可以经过平移将三次函数的拐点(即三次函数的对称中心点)移到原点处,使问题简化,从而较为简单地解决问题.此时三次函数都可化为y=ax3+px(a≠0),以下称该型为标准型三次函数.过程如下:
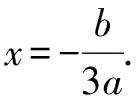
另上面也可这样变形:
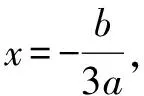
此时只须上下平移即可变为标准型三次函数.
经过以上分析,要解决三次函数问题,实际上解决标准型问题即可.同样的思维方法用在有关三次函数问题命题时有很好的帮助.一方面可以在标准型上研究,然后推广到一般情形,另一方面也可以命好题后放到标准型上继续研究.
不妨假设标准型三次函数的三次项系数a>0,则显然有以下性质:
1.函数为奇函数,原点为其对称中心点;
2.当p≥0时,函数在R上为增函数,没有极值;




(1)若对任意的m∈(t,x2],线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
(2)若存在点Q(n,f(n)),x1≤n 分析(1)在过点M的直线中,除平行于x轴外恰好还有一条与曲线相切,且切点在O点与N点之间.此时如果斜率继续增大,在P点两侧均有交点.可见,相切时的切点是线段MP是否与曲线有异于M,P的公共点的临界点.曲线在P处的切线斜率为f′(m). m=-2时即为M点,故m=1. (2)若m∈(0,2],只要取Q为P关于原点的对称点,因为f(x)为奇函数,显然PQ线段过原点,而原点在曲线上,所以m∈(0,2]符合题意. 若m∈(-2,0],因为-2 本题若为普通三次函数(如09福建卷)则明显加大难度了,因为函数的图象不清,不能应用数形结合,特别是(2)问难度就更大了,所以原题(09福建卷)只要求写出结果,而不要求证明. 该题用很基本的三次函数,但却考查了科学严谨的数学分析的思想方法,对中学阶段来说属灵活性,难度都较大.试题有较好的区分度,不过有不足的地方就是起点门槛高,对不能理解题意的考生基本得不到分数. 分析本题关键在两点: 1是切线l1上两倍的切点横坐标和切线与曲线另一交点横坐标和为零;(把切点当两个点看,即有切线与曲线交点的横坐标和为零,如本题2xP1+xP2=0) ∴a(x-x1)2(x+2x1)=0.∵x≠x1, ∴x+2x1=0,即x2+2x1=0,即有2xP1+xP2=0. 另一方面: 拐点处切线方程为:y=px,与f(x)联立方程有: 事实上,对上述的第一点有:对三次函数y=ax3+px(a≠0),如果与直线y=kx+b有三个交点,则三个交点的横坐标和为零.特别地,当直线与曲线相切时,切点用两点计算.联立两方程,因为ax3+px=kx+b,即有ax3+ (p-k)x-b=0,由x2项的系数为零,根据韦达定理容易得到:x1+x2+x3=0. 把上述推广到一般情形有:对一般三次函数y=ax3+bx2+cx+d(a≠0),如果与直线y=kx+b有三个交点,则三个交点的横坐标的平均值为三次函数拐点的横坐标.(如果直线与曲线相切,则切点用两点计算)可以把这一性质设计成试题,让考生猜想,同样的,考生不容易观察到,对数学思维有很高的要求.