三类特殊图的(强)彩虹连通数

赵燕,柴航

(泰州学院数理学院,江苏 泰州 225300)

1 引言

本文考虑的图为有限无向简单图.Chartrand等人[1]在2008年首次提出了彩虹连通性的概念.设图G=(V,E)是一个非平凡的连通图,在G上定义一个边染色c:E→{1,2,···,t},t∈N,其中相邻的边可以染相同颜色.如果这条路上的任意两条边均染不同颜色,称图G的一条路是彩虹路.如果在图G的任意两个顶点间都存在一条彩虹路,就称图G是彩虹连通的.对于一个连通图G,保证它是彩虹连通所需的最少颜色数就是G的彩虹连通数,记为rc(G).彩虹连通不仅是一个自然的组合概念,而且在网络中也有着重要的应用.事实上,它的提出起源于政府机构之间的信息安全传递.当人们在机构之间传递信息时,一方面希望所用的密码个数足够得少以便于管理;另一方面,又需要足够多的密码,使得任何两个机构之间至少存在一条信息安全路(路的不同段分配不同密码),以防止入侵者破坏.可以用图来表示这个信息传递网络.如果用边染色表示密码,那么最少的密码个数就是图的彩虹连通数.

基于彩虹连通数的概念,Chartrand等人[1]又提出了强彩虹连通数的概念.给定图G中的两个点u,v,一条彩虹(u,v)-测地线是指图G中一条长度为d(u,v)的彩虹路,其中d(u,v)表示图G中u,v的距离.如果在图G的任意两个顶点间都存在一条彩虹测地线,就称图G是强彩虹连通的.对于一个连通图G,保证它是强彩虹连通所需的最少颜色数就是G的强彩虹连通数,记为src(G).

Chakraborty等人[2]证明了给定一个图G,判定rc(G)=2是NP-完全的,特别的,计算一个图的rc(G)是NP-困难的.Chartrand等人[1]得到了一些特殊图类的彩虹连通数.例如,rc(G)=src(G)=1当且仅当G是完全图,rc(G)=src(G)=m当且仅当G为一棵m条边的树,一个顶点数大于3的圈的 (强)彩虹连通数为.注意到,对于任意连通图G,diam(G)≤rc(G)≤src(G)≤m,其中diam(G)表示图G的直径,m表示图G的边数.同时注意到,若H为G的连通生成子图,则rc(G)≤rc(H).更多关于彩虹染色的结果参考文献[3-6].

本文研究了两类特殊图的彩虹连通数.首先给出一些定义.2n个点的太阳图是在n个点的圈图的基础上,每个点处再悬挂一条边.令图G有m个顶点,图H有n个顶点,G和H的日冕(corona)(用G⊙H表示)定义为一个图,取一个G的复制和m个H的复制H1,···,Hm,在G的第i个点和H的第i个复制的每个点均连边.由定义可知,G⊙H有m(1+n)个顶点.对任意两个图G和H显然有G⊙H?H⊙G.

接着给出本文需要用到的一些彩虹连通数的结果.

引理1.1[7]令n≥2,则扇图(即Pn∨K1)的彩虹连通数为：

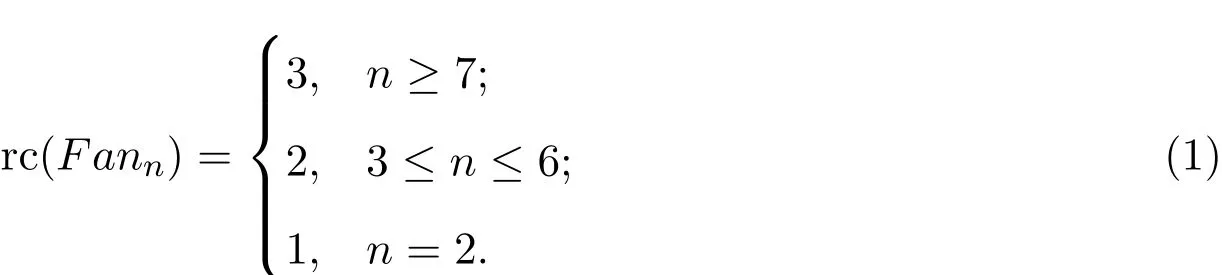
引理1.2[7]令n≥2,则扇图(即Pn∨K1)的强彩虹连通数为：

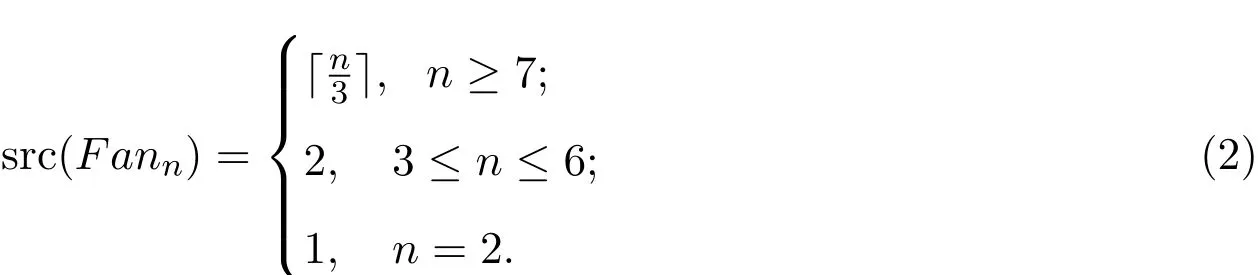
引理1.3 令n≥3,则太阳图Sn的(强)彩虹连通数为：

2 主要结果

定理2.1 令G=(Pt1∪Pt2∪···∪Pts)∨K1,其中,2≤ t1≤ t2≤···≤ ts,则

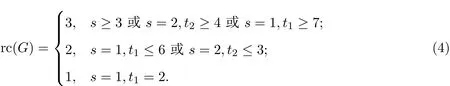
证明令

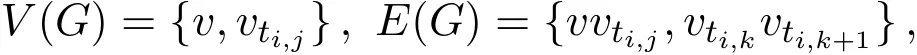
其中

s=1的情形即引理1.1,因此下设s≥2.首先令s≥3.定义一种染色方式

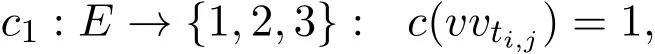
若1≤i≤s,1≤j≤ti,且j为奇数;c(vvti,j)=2,若1≤i≤s,1≤j≤ti,且j为偶数;其余边染3色.易证图中任意两点均有彩虹路连接,因此rc(G)≤3.假设用两种颜色染色,由于

并且vt1,i和vt2,j(vt3,k)只有一条2长路,因此得到

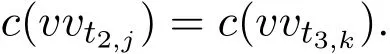
此时,vt2,j和vt3,k无彩虹路.因此rc(G)=3.

当s=2,t2≥4时,仍采用染色方式c1,可以保证图中任意两点均有彩虹路连接,因此rc(G)≤3.假设用两种颜色染色,由于d(vt1,i,vt2,j)=2,并且vt1,i和vt2,j只有一条2长路,因此得到

其中1≤j,k≤t2,j̸=k.此时,vt2,1和vt2,t2无彩虹路.因此rc(G)=3.

当s=2,t2≤3时,定义一种染色方式

c2:E→{1,2}:c(vvt1,1)=c(vvt1,2)=c(vvt1,3)=c(vt1,1vt1,2)=c(vt2,1vt2,2)=1,其余边染2色.易证图中任意两点均有彩虹路连接,因此rc(G)=2.

定理2.2 令G=(Pt1∪Pt2∪···∪Pts)∨K1,其中2≤ t1≤ t2≤ ···≤ ts,s≥ 2,则

证明令

其中

s=1的情形即引理1.2,因此下设s≥2.考虑vti,p和vtj,q(i̸=j).由于它们只有一条测地线,为保证vti,p和vtj,q有彩虹测地线,

由引理1.2知,如果c(vvti,p)=c(vvti,q),则dPti(vti,pvti,q)≤2.因此

另一方面,类似于引理1.2,可以定义一种染色方式保证图中任两点有一条彩虹测地线.因此,定理得证.

定理2.3 设n为偶数,令G=Cn⊙K2,则rc(G)=

证明 令n=2k.设

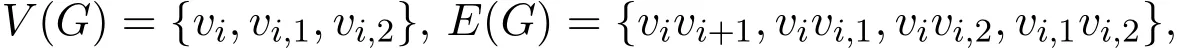
其中1≤i≤n.首先证明rc(G)≤k+3.定义一种染色方式

c:E → {1,2,···,k+3}: c(vivi,1)=k+1(1≤ i≤ n), c(vivi,2)=k+2(1 ≤ i≤ n),c(vi,1vi,2)=k+3(1≤i≤n), c(vivi+1)=i(1≤i≤k), c(vivi+1)=i−k(k+1≤i≤n).

易证图中任意两点均有彩虹路连接,因此得证.

下面证明rc(G)≥k+3.反证,假设G使用一种k+2种颜色的边染色方式使得图中任意两点有一条彩虹路连接.

首先得到如下的论断:圈中两条同色边只能是相对边.反证,假设

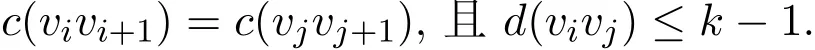
为保证vi,1和vj+1,1存在一条彩虹路,d(vivj)=k−1.不妨假设 c(v1vn)=c(vk+1vk+2).考虑v1,1(v1,2)和vk+1,1(vk+1,2).易得

于是有

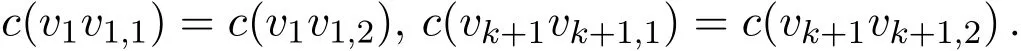
不妨假设

为保证vk+1,1和vk,1,vk+1,1和vk,2均有彩虹路,色k和k+2不能同时出现在vk悬挂的三角形中. 考虑v1,1和vk,1(vk,2),此时v1,1vk,1-彩虹路只可能走vkvk,1或者vkvk,2vk,1. 如果走vkvk,1,v1,1vk,1必为色k或k+2.如果为色k,为保证v1,1和vk,2有彩虹路,vk,1vk,2染k+2或者vkvk,2染k或k+2,此时vk+1,1和vk,1无彩虹路,矛盾.如果为色k+2,为保证v1,1和vk,2有彩虹路,vk,1vk,2染k或者vkvk,2染k或k+2,此时vk+1,1和vk,1仍无彩虹路,矛盾. 如果走v1,1vk,2vk,1,v1,1vk,2和vk,2vk,1必为色k和k+2,此时vk,2和vk+1,2无彩虹路,矛盾.

为保证v1,1和vk+1,1有彩虹路,不妨假设

由上述论断知,色k+1在圈中至多出现一次,k+2也至多出现一次.根据色k+1和k+2是否在圈中,分如下三种情形考虑.

情形1 色k+1和k+2同时在圈中.此时

进一步,只能边vk+1vk+2染色k+1,边vnv1染色k+2.由上述论断知,

考虑v1,1和vk,1,如果vkvk,1染色k,为保证v1,1和vk,2有彩虹路,则vk,1vk,2染k+2或者vkvk,2染k或k+2,此时vk,1和vk+1,2无彩虹路,矛盾;如果vkvk,1染色k+2,类似vkvk,1染色k的情形;如果vkvk,1不染色k和k+2,则vkvk,2和vk,2vk,1必为色k和k+2,此时vk,2和vk+1,2无彩虹路,矛盾.

情形2 色k+1在圈中,色k+2不在圈中(色k+2在圈中,色k+1不在圈中类似).此时

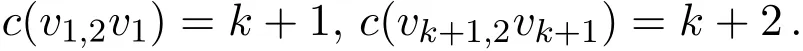
进一步,只能vk+1vk+2染色k+1.由上述论断得

类似于情形1,考虑v1,1和vk,1,均会得出矛盾.

情形3 色k+1和k+2均不在圈中.

由上述论断知,c(vivi+1)=i−k(k+1≤i≤n−1).此时

类似于情形1,考虑v1,1和vk,1(vk,2),色k+2或者色k出现在vk悬挂的三角形中两次,或者色k和k+2同时出现在vk悬挂的三角形中,均会得出矛盾.

推论2.1 设n≥4为偶数,令G=Cn⊙P3,则rc(G)=

证明设

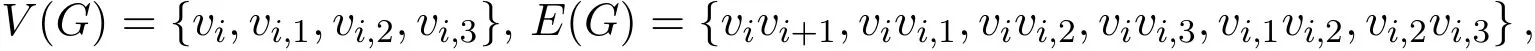
其中1≤i≤n.在定理2.3的染色基础上,添加新的染色

通过类似定理2.3的讨论,可以得证.

定理2.4 设n≥4为偶数,令G=Cn⊙K2,则src(G)=n+1.

证明设

其中1≤i≤n.首先证明src(G)≤n+1.定义一种染色方式c:E→{1,2,···,n+1},其中

易证图中任意两点均有彩虹测地线连接,因此c为强彩虹连通染色.

下证

用反证方法,假设src(G)≤n.由于

推论2.2 设n≥4为偶数,令G=Cn⊙P3,则src(G)=n+1.

证明设

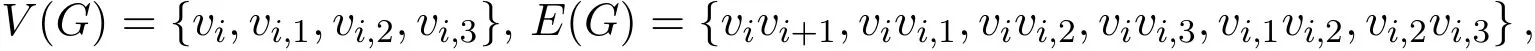
其中,1≤i≤n.在定理2.4的染色基础上,添加新的染色

通过类似定理2.4的讨论,可以得证.