放矿场动力学响应机理研究的LBM-DEM耦合方法
2018-10-10常宝孟杜翠凤初晓峰
常宝孟 杜翠凤 韩 斌 李 涛 初晓峰
(北京科技大学土木与环境工程学院,北京100083)
自然崩落法具有生产能力大、便于组织管理、作业安全及开采成本低等优点,是唯一能与露天开采经济效益相媲美的高效地下采矿方法[1-4]。自然崩落法放矿是在崩落围岩覆盖条件下进行的,覆岩中的废石极易掺杂于矿石中,并与矿石一起经放矿口放出,从而造成放矿贫化。此外,放矿控制不当可能造成矿岩崩落不均匀,易造成放矿口堵塞及井下空气冲击波等危害,严重影响井下人员与设备安全及矿山生产效益,因此有必要对放矿过程进行理论研究。
自然崩落法放矿过程的本质是崩落矿岩在放矿漏斗内运动的动力学过程[5],国内外学者提出的椭球体放矿、类椭球体放矿及随机介质放矿等放矿理论主要是基于放矿运动学方面的研究,其研究前提是将崩落矿岩视为理想散体,与矿山生产实际存在出入,因而具有一定的局限性和不可靠性。目前,国内外关于放矿动力学的研究主要有:赖森华等[5]在分析放矿过程中矿岩移动规律的基础上,建立了矿岩块体力学模型和相应的动力学方程,从理论上对放矿动力学过程进行了探讨;王昌汉[6]根据实验研究结果,建立了松散矿岩从漏斗口均匀放出时的力学方程,从散体力学角度对放矿力学体系进行了完善;F Melo等[7-8]基于Bergmark-Roos理论分析了放矿过程中矿岩块体的受力状态,建立了放出体极坐标运动方程。由于放矿过程本身的复杂性及研究手段的局限性,放矿动力学相关研究成果较少且发展缓慢。
针对自然崩落法放矿研究,离散元法(Discrete Element Method,DEM)是岩土力学中最常用的有效模拟手段。但由于受模拟颗粒数量及计算机性能的限制[9],难以在全域上采用离散颗粒进行模拟。按照美国ASTM(Unified Soil Classification System)岩土颗粒粒级分类标准[10],相较于粒径单向尺寸大于1 m的矿岩,颗粒直径小于19 mm的碎石可视为细颗粒。刘传平等[11-12]基于“拟流体”思想,通过颗粒斜槽流实验获得了颗粒流黏性的本构关系,其数学模型预测值与实验结果的相对误差在13%以内,表明颗粒流拟非牛顿流体研究是可行的。而格子Boltzmann法(Lattice Boltzmann Method,LBM)作为一种新兴的流体数值模拟方法,具有高并行性及能够处理复杂边界条件等显著优势,近年来在多相多组分流、粒子悬浮流及多孔介质流等方面得到了广泛的发展和应用[13-15]。根据上述理论与研究,本研究将自然崩落法放矿过程中大块散体矿岩及碎石细颗粒分别视为离散体与非牛顿流体,并基于LBM-DEM耦合方法实现自然崩落法放矿过程模拟,从动力学角度对放矿场内崩落矿岩的力学响应机理进行分析,为放矿理论研究提供新的研究思路与技术支持。
1 LBM-DEM耦合框架
1.1 LBM非牛顿流体处理
在LBM粒子速度离散模型中,典型的二维D2Q9模型(如图1所示)的离散速度ei为:

式中,C=dx/Δt为格子速度,Δt为时间步长。

为将碎石细颗粒拟作非牛顿流体,需对LBM方程进行非牛顿流体化处理。在处理流固耦合的问题时,LBM方程标准形式为[15]:
式中,(fix,t)为t时刻位于x处以离散速度ei运动的粒子分布函数;τ为无量纲松弛时间;fieq为局部平衡态方程。D2Q9模型对应的平衡态分布函数具有如下形式:

式中,ωi为数值积分公式的权系数,为格子声速;u为速度。宏观层面的流体密度ρ、速度u和压力P可由粒子分布函数的零阶和一阶速度矩定义:

在低马赫数假设前提下,通过Chapman-Enskog展开由式(2)格子Boltzmann方程可正确恢复出Navier-Stokes方程,并得到非牛顿流体黏性与模型参数的关系[16]为:

式中,v为非牛顿流体黏度;e为应变率;τ*与τ0分别为非牛顿流体与牛顿流体松弛时间。
1.2 流体—移动颗粒边界耦合控制策略
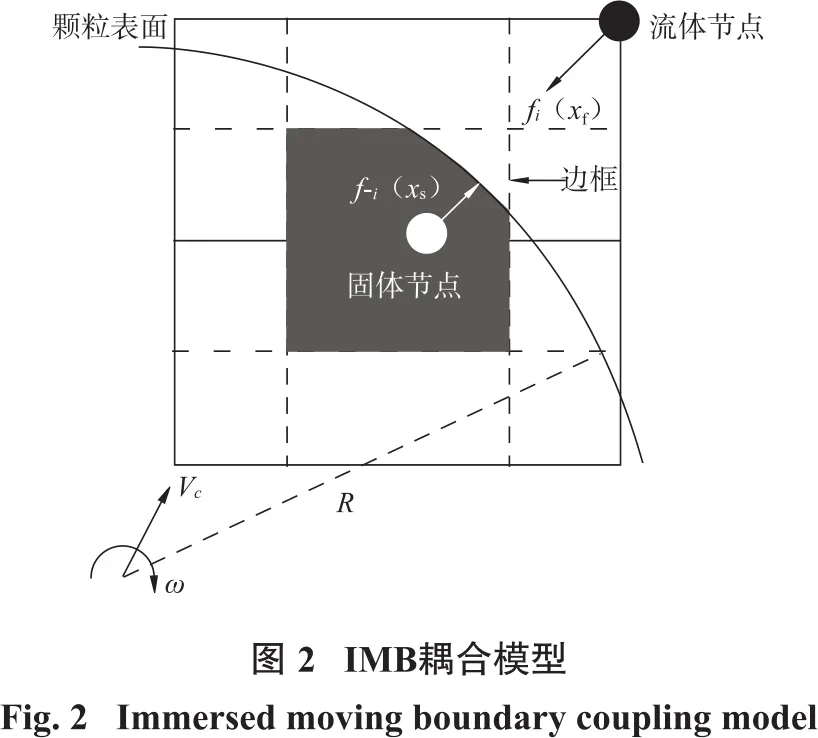
要实现放矿场内流体与离散颗粒的耦合框架,重点在于解决细颗粒流与移动散体矿岩的边界耦合问题。Noble等[17]提出针对LBM-DEM耦合的浸入运动边界法(Immersed Moving Boundary,IMB)。为解决流固边界耦合动量不连续性问题,并使移动颗粒受力计算更平顺,引入新物理参数格子固含率ε,其取值取决于固体节点所覆盖的节点单元比例,图2中固体节点的格子固含率ε为填充区域与其边框的面积比值,fi(xf)为流体节点,f-i(xs)为固体节点。
针对IMB法,通过引入一个与格子固含率有关的加权函数β来修正LBM,其表达式为:

对应式(7),修正后的LBM方程为:
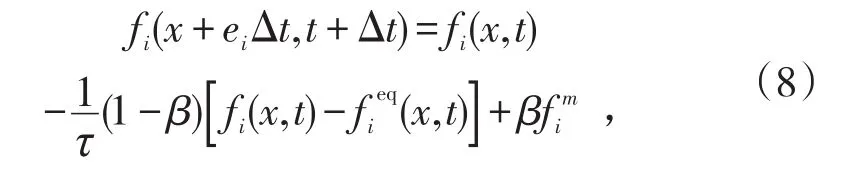
通过在LBM修正方程中引用非牛顿流体松弛时间τ*,可解决碎石细颗粒流拟非牛顿流体及流体与移动颗粒边界耦合的问题。
2 流体与离散颗粒耦合力
自然崩落法放矿过程中,散体矿岩颗粒的运动存在随机性与突发性,难以对每一块体每一时刻的运动状态和力学作用过程进行精确描述和分析。根据崩落矿岩的散体流动性及放矿场的边界条件,可对放矿场内矿岩颗粒在放矿过程中的受力状态进行分析,如图3所示。

放矿场内单个矿岩颗粒运动遵循牛顿第二运动定律,矿岩颗粒在重力mg作用下,与细颗粒流及其他相邻矿岩颗粒间存在摩擦力Ff,且Ff为阻尼作用,阻碍矿岩块体向放矿口运动。除此之外还存在碰撞作用,由于块体间的碰撞作用存在随机性,因而将其简化为垂直于Ff方向的合力N。根据图3的受力分析,放矿场内单个矿岩颗粒的动力学方程可表达如下:
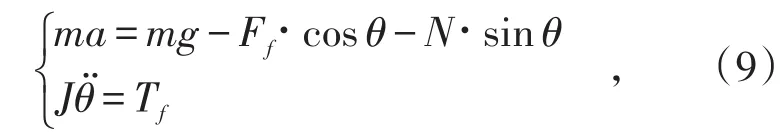
式中,m和J分别为矿岩颗粒质量与惯性矩;θ̈为角加速度;Ff和Tf分别为作用于矿岩颗粒上的总摩擦力与总力矩。流体粒子与固体颗粒交互作用时,两者间将产生动量交换,根据流体粒子与固体颗粒之间的动量交换可计算作用力。按照动量定理,颗粒受到的总摩擦力和力矩分别为:

式中,β为加权函数。
获得作用于颗粒上的力和力矩后,分别对颗粒的运动方程进行离散求解,散体颗粒运动方程为:

式中,Mp和Fp分别为颗粒质量和作用于颗粒上的总力;up为颗粒运动速度;xc为颗粒质心。其中,t时刻颗粒受到的作用力、力矩和颗粒速度三者平均值为:

式中,ϕ=Fp,Tf,up.
3 算例:自然崩落法单漏斗放矿试验
3.1 计算参数及数值模型
国内某矿山已探获铜金属量为480万t,矿化带长 2 300 m,宽 600~800 m,面积约 1.09 km2,呈穹窿状。由于该矿具有岩层破碎、矿石品位较低、矿体相对较为厚大等特点,故采用自然崩落法全地下开采。开采区矿体及围岩主要由石英二长斑岩与闪长玢岩组成,根据开采技术条件研究成果整理,矿体及围岩力学参数见表1。

在生成自然崩落法放矿数值模型时,需对放矿场内的不同块度矿岩进行分类处理:根据颗粒斜槽流实验结果[12-13]将细颗粒流视为非牛顿流体,在时间与空间统计平均意义下,其细观结构不需考虑,并通过LBM方法处理;大块散体矿岩在放矿漏斗内的运动视为离散体运移,并通过DEM方法模拟其运动状态。由于在实际放矿场中,崩落矿岩颗粒是非球形的,且块度大小不均,此类复杂介质通常通过定义当量直径Dp来表示其中颗粒的大小,Dp可根据不同的统计平均方法确定。在此统计平均意义下,崩落散体矿岩可表示为按高斯分布的直径为Dp的二维圆盘介质(颗粒粒级服从高斯分布)。考虑模型计算量和计算精度的要求,散体矿岩及流体域参数分别按表2、表3选取。


根据第1节中LBM-DEM耦合框架,分别将放矿场内细颗粒流与大块崩落矿岩通过LBM与DEM模拟,利用Fortran语言编写程序代码,按矿山放矿场参数设置模型参数,并在Visual Studio平台对算例代码进行编译。生成的单漏斗放矿耦合模型如图4所示。

3.2 模拟结果及分析
图5为编译程序经Tecplot软件处理后获得的放矿场内不同时刻压力分布云图。从图5中可以看到,在时间t分别为5 s、10 s及15 s时,放矿口周边压力较大,一直保持在3.002 5×107~3.007×107N水平,而放矿口上部压力较小,在2.991×107N左右,且放矿场内压力随崩落矿岩的放出表现为脉动分布形式。其主要原因在于崩落矿岩从放矿口放出时存在松散和压缩2种变形,放矿口上部为松散变形区,矿岩压力较小,周边为压缩变形区,矿岩压力较大。此外,液—固两相流中颗粒相的细观结构与宏观力学特性均十分复杂,流场中离散颗粒是其运动的基本单元,在放矿过程中表现为随机脉动的运动形式,而细颗粒流拟为非牛顿流体,其动力学特性在统计平均意义下具有宏观上的连续性与规律性,因而会出现放矿场内压力脉动分布现象。

为进一步研究放矿场内不同位置的压力分布特征,分别以放矿口水平为x轴,以放矿口轴线为y轴建立直角坐标系,分别取A(-5,1)、B(0,10)、C(0,50)3点进行监测,压力监测结果如图6所示。

根据图6可知,放矿口处监测点A压力在3.002 5×107~3.007×107N间波动,放矿口轴线上B、C2点压力值波动区间比较接近,区间为2.993 5×107~2.998×107N,A点压力值明显大于B、C2点。上述压力分布特点原因在于放矿场内颗粒介质的离散性与随机性主要通过颗粒间的摩擦与碰撞产生动量传递与能量耗散。临近放矿口处,矿岩颗粒运动速度快,矿岩间的碰撞与摩擦作用明显,而远离放矿口位置的颗粒运动速度较慢,矿岩间碰撞阻尼作用较弱。放矿场内矿岩动力学响应机理研究结果与文献[5]、[18]等研究结论一致,并对研究放矿成拱原因、放矿场边界压力及控制底部结构压力等具有指导作用。
4 结论
(1)将碎石细颗粒流与大块崩落矿岩分别视为非牛顿流体与离散体,并分别通过LBM与DEM模拟,基于LBM-DEM耦合框架可以很好地实现自然崩落法单漏斗放矿模拟,同时有效降低离散元模拟规模,为放矿模拟提供了新的研究手段。
(2)从放矿动力学角度对放矿场内单个散体矿岩进行受力分析,得出放矿过程中其主要受重力及颗粒间的碰撞与摩擦阻力作用。按照动量定理,推导出颗粒总摩擦力及力矩计算公式,并通过对颗粒运动方程进行离散求解,得出相应的颗粒运动方程。
(3)根据本研究提出的计算分析方法,得出矿岩放出过程中放矿口上部存在松散与压缩2种变形,放矿口周边压力在3.002 5×107~3.007×107N水平,放矿口上部压力在2.991×107N左右,且放矿场内压力因散体矿岩的随机脉动形式随时间做脉动分布。
(4)通过设置不同监测点,得出A、B、C3点处压力值均在一定区间内波动,且A点压力要明显大于B、C2点,与放矿场内颗粒介质的离散性与随机性主要通过颗粒间的摩擦与碰撞产生动量传递与能量耗散有关。
