陶瓷大板圆形轨迹加工工艺研究

2018-10-10徐斌

佛山陶瓷 2018年9期

关键词：节距大板磨头

徐斌

（广东科达洁能股份有限公司，佛山528313）

关健词：陶瓷大板；长幅摆线；圆形轨迹；磨头

1 前言

2018年佛山陶瓷展会在潭洲举行，陶瓷大板是展会的热点，各个厂家争相展出大规格的陶瓷砖。瓷砖已经进入了“大”时代，这也推动了瓷砖行业的进一步发展。这次展会上，展出最大规格的瓷砖是3200 mm×1600 mm。

陶瓷大板的特点是规格大[1]，而石材大板的特点也是如此。因此，石材大板深加工工艺对陶瓷大板的加工具有很强的借鉴意义。国内外石材大板抛光工艺发展到今天，不再是局限于摆动式抛光，之字形加工轨迹[2-3]，还有圆形加工轨迹、八字形轨迹等等。石材大板圆形轨迹加工工艺是在2015年开发并应用，2015年湖南卓迪机械有限公司研发了其设备并应用生产，但是并未在石材行业之内普遍推广和应用。至今应用最为广泛的还是摆动式抛光工艺，之字形加工轨迹。原因是石材边缘不规则，造成尺寸不规格。加工过程中会出现漏抛现象，由于没有理论数据，无法准确的掌握瓷砖进给与圆形轨迹之间的匹配关系，限制了这种工艺在石材行业的发展。

本文在借鉴石材大板圆形轨迹加工设备的基础上，分析陶瓷大板圆形轨迹加工原理，建立陶瓷大板研抛复合运动轨迹方程。得出陶瓷大板进给速度、横梁圆形轨迹运动与磨头加工覆盖率之间的匹配关系。研究结果对陶瓷大板圆形轨迹工艺的应用提供了理论基础，为设备的设计提供理论数据。同时也为圆形轨迹加工工艺在石材行业的推广和应用，提供理论支持。

2 陶瓷大板圆形轨迹加工工作原理

在借鉴湖南卓迪机械有限公司研发的石材大板圆形轨迹加工设备的基础上，分析陶瓷大板圆形轨迹加工工作原理。如图1所示。磨头安装在横梁上，横梁规定在曲柄上[4]，曲柄安装在支撑座上。从图上看出，实质上是一个双曲柄结构。两端曲柄的尺寸是相同的，双曲柄驱动着横梁上的磨头做圆周运动。因此磨头的运行轨迹和两端的曲柄是一样的，也是圆形轨迹。该运行原理形式与蒸汽式火车的驱动轮系统运行原理类似。陶瓷大板在磨底下做直线进给运动。

3 陶瓷大板研抛轨迹方程

图1显示的是横梁驱动磨头运动之后，磨头中心线所做的运动轨迹，其轨迹是一个圆。但是没有加上陶瓷大板的进给运动。陶瓷大板研抛轨迹是指横梁圆形轨迹运动，以及与陶瓷大板进给运动复合而成的运动，在陶瓷大板表面上划擦出来的运动轨迹。因此，陶瓷大板研抛轨迹是一种复杂的运动轨迹。如图2所示，这种轨迹是由牵连运动，也就是陶瓷大板的进给速度v；相对运动，也就是磨头中心点m绕着圆形轨迹中心点m所作的旋转运动。从而得到磨头中心点m在陶瓷大板上的绝对运动轨迹。

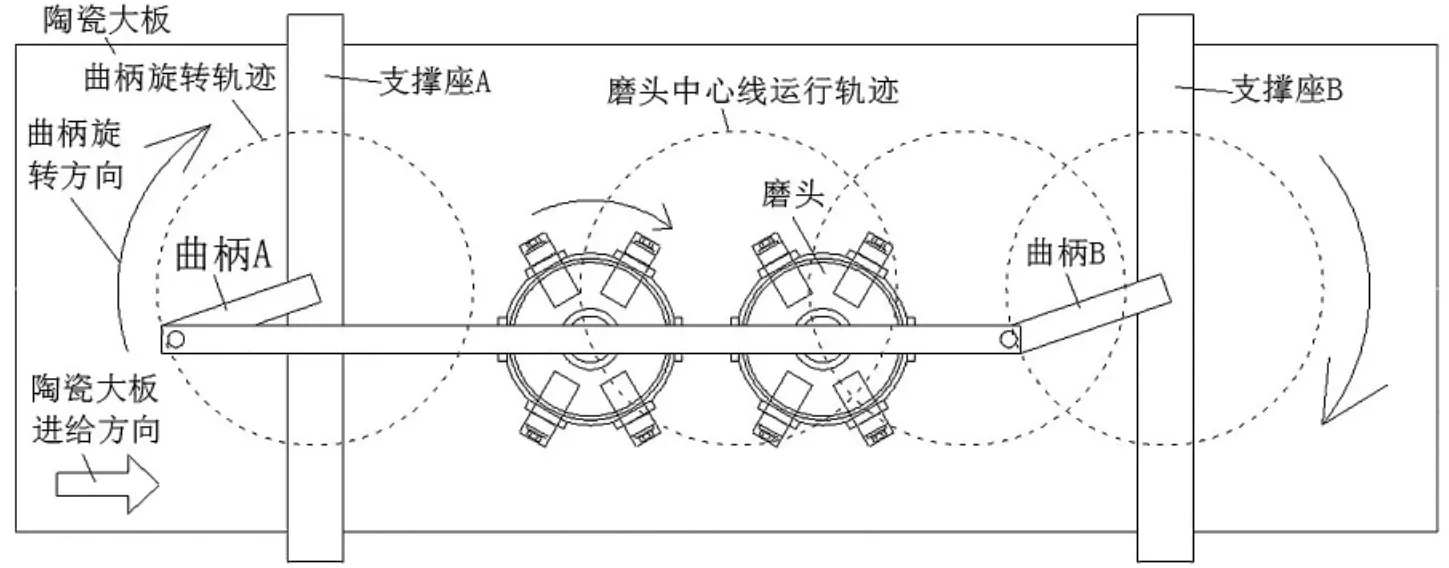
图1 陶瓷大板圆形轨迹加工工作原理图

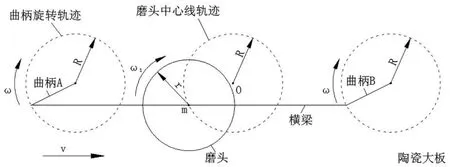
图2 陶瓷大板圆形轨迹加工运动简图

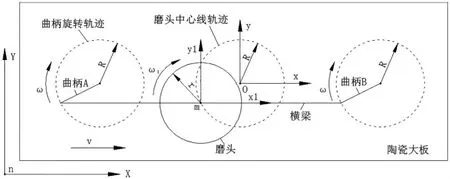
图3 陶瓷大板研抛运动坐标系

为了便于研究，首选要对上述各种运动建立坐标系。

图3中，将陶瓷大板抛光机机架上的参考系nXY成为固定参考系，简称定系。将因曲柄运动而驱动横梁做圆形运动得到的圆形轨迹的参考系Oxy称为动参考系，简称动系。被观察的磨头中心点m称为动点。动点相对于定系的运动称为该点的绝对运动；动点相对于动系的运动，称为相对运动；动系相对于定系的运动称为牵连运动。

为了描述磨头中心点m在陶瓷大板表面的运动轨迹，动系取在O点处，定系取在机架，这样上述的三种运动就随之确定。磨头中心点m的绝对运动就是陶瓷大板表面的运动轨迹，该轨迹是沿旋轮线的运动。相对运动是圆周运动，是磨头中心点m绕着中心点O的圆周运动。牵连运动是陶瓷大板的进给直线运动。

磨头中心点m在陶瓷大板表面上的合成运动轨迹曲线，下面采用作图法描点绘出。

在图4中假设u、v均为等速运动，图中R为曲柄半径；ω为曲柄旋转角速度；v为陶瓷大板直线进给速度；u（=Rω）为磨头中心m相对于横梁驱动其形成的圆周轨迹线的圆周线速度。

磨头中心点m在沿着圆周轨迹线（图4中虚线圆）旋转前进的过程中，圆周轨迹线圆心所在的位置原为O0，磨头中心点在该圆周轨迹线上的端点为m0。圆周轨迹线按照图中箭头所示的方向转过△ф1的角度时，圆周轨迹线的中心由O0前进至O1，这是圆周轨迹线正转的情况。此时，磨头中心点的位置由m0移动到m1；当圆周轨迹线连续再转过△ф1时，圆周轨迹线的中心将再前进一段距离到O2，此时磨头中心点的位置由m1移动到m2，如此继续下去，当陶瓷大板走过距离S，即圆周轨迹线的中心经过 O1、O2、O3......至 On时，磨头中心点 m在陶瓷大板表面的轨迹即为m1、m2、m3......mn所连接形成的曲线。该曲线为摆线。如果S为圆周轨迹线旋转一周时陶瓷大板直线进给的距离，则此时磨头中心点m旋转一周后运动估计也完成了一个形成周期，如此继续下去，周而复始。图中S＜2πR。

下面分别建立轨迹的方程，建立如图5所示的坐标系。设坐标轴Y上的磨头中心m，以角速度ω经过t秒钟转动之后，其角位移为ф，此时圆周轨迹线的中心移动的距离为x0，磨头中心的位置移动到m1点，点m1的水平位移为x，垂直位移为y。

（1）磨头中心点m的旋转运动方程（相对运动）

式中：R——圆周轨迹半径（mm）

ф——圆周轨迹旋转的角位移（rad）

（2）陶瓷大板的直线进给运动方程（牵连运动）

式中：v——陶瓷大板的直线进给运动速度，（m/min）

（3）磨头中心点m在陶瓷大板表面的轨迹曲线方程（绝对运动）

式中：R——圆周轨迹半径，（mm）；

ф——圆周轨迹旋转的角位移，（rad）；

x0——圆周轨迹线的中心移动的距离，（mm）。

将 x0代入（3）式得：

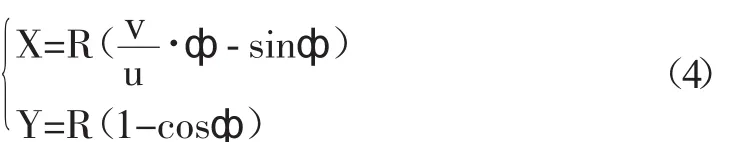
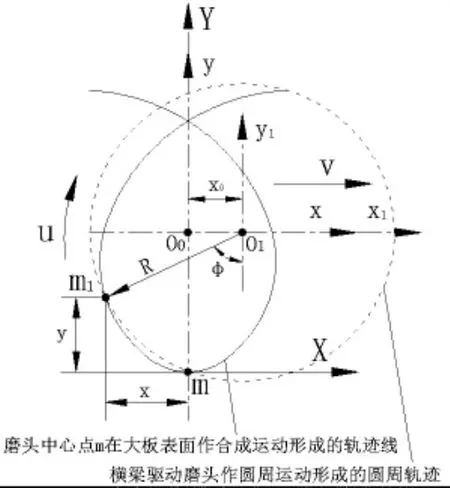
图5 磨头中心点轨迹分析图

4 陶瓷大板研抛轨迹的性能特征

从磨头中心点m在陶瓷大板表面的轨迹曲线方程（4）得知，磨头中心点m在陶瓷大板表面的轨迹曲线形状与圆周轨迹半径R、圆周轨迹线旋转速度u、陶瓷大板直线进给速度v有关。由于R、u、v不同，磨头中心点m在陶瓷大板表面的轨迹曲线具有以下特征：

式（5）是标准的摆线公式，S=2πR。其轨迹如图6所示。标准摆线的轨迹是一个圆弧线，在交接之处转折一下。

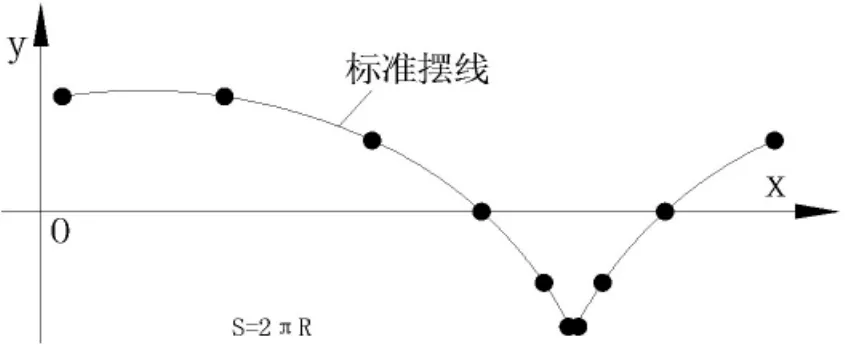
图6 标准摆线轨迹

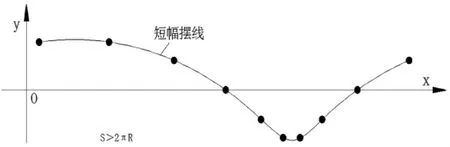
图7 短幅摆线轨迹

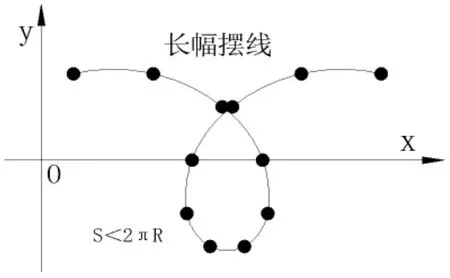
图8 长幅摆线轨迹

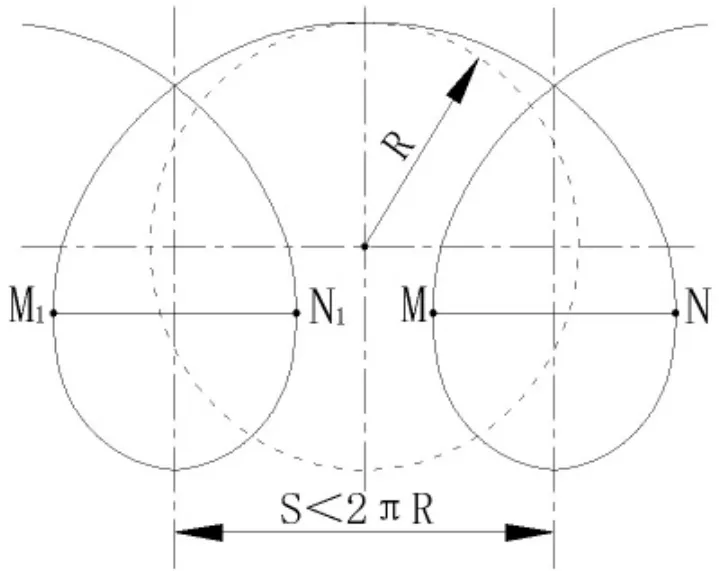
图9 磨头中心点m在陶瓷大板表面的运动轨迹曲线

这种长幅摆线具有一个绕扣，如图9所示。图中MN为绕扣的横弦。当值越小时，绕扣的横弦就会越大。当v=0时，则绕扣就是一个整圆，最大的横弦等于2R。

综上分析，得出标准摆线、短幅摆线不是适合做磨头中心点m在陶瓷大板表面的运动轨迹曲线。因为标准摆线、短幅摆线会在陶瓷大板的表面形成空白区域。长幅摆线轨迹是最适合做磨头中心点m在陶瓷大板表面的运动轨迹曲线。长幅摆线有一个绕扣，这种摆线就像一个个拉开的圆环，可以有力的保证磨头运动轨迹在陶瓷大板表面的覆盖，保证抛光的均匀性。

5 陶瓷大板研抛轨迹的运行速度

磨头中心点m沿着圆周轨迹线旋转一周的过程中，所经各处的速度是不同的。对（4）式中的时间求导得：

磨头中心点m的绝对运行速度：

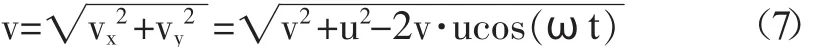
从（7）式可知，磨头中心点m处于在陶瓷大板表面的运动轨迹曲线（摆线）最低位置，也就是ωt=2πn时，绝对速度最小，vmin=v-u。当磨头中心点m处于在陶瓷大板表面的运动轨迹曲线（摆线）最高位置，也就是ωt=（2n+1）π时，绝对速度最大，vmax=v+u。

由此可见，磨头中心点m的运行速度，随着时间作周期性的变化。陶瓷大板作等速进给运动，也就是直线前进速度v是常量，则对磨头不产生加速度的影响。磨头中心点m处的加速度，仅有其沿着圆周轨迹旋转运动而产生。磨头中心点m处的加速度数值由下式表示：

式中：R——圆周轨迹半径，（mm）；ω——圆周轨迹旋转角速度，（rad/s）。

6 陶瓷大板研抛工艺参数的确定

（1）节距。

磨头中心点m沿着圆周轨迹旋转运动与陶瓷大板直线进给运动的合成运动轨迹是长幅摆线。在陶瓷大板表面上连续的研抛轨迹，如图10所示。从图中看出，连续的加工轨迹好似一个个拉开的圆环，实质上这是平面螺旋线。

如图中所示，相邻的两个研抛轨迹线在中线上对应两点间的轴向距离称为节距，用S表示。节距又称为进给量。也就是磨头中心点m沿着圆周轨迹旋转一周，陶瓷大板的进给距离。这个进给距离小于圆周轨迹的周长时，才会形成长幅摆线轨迹，也就是S＜2πR。

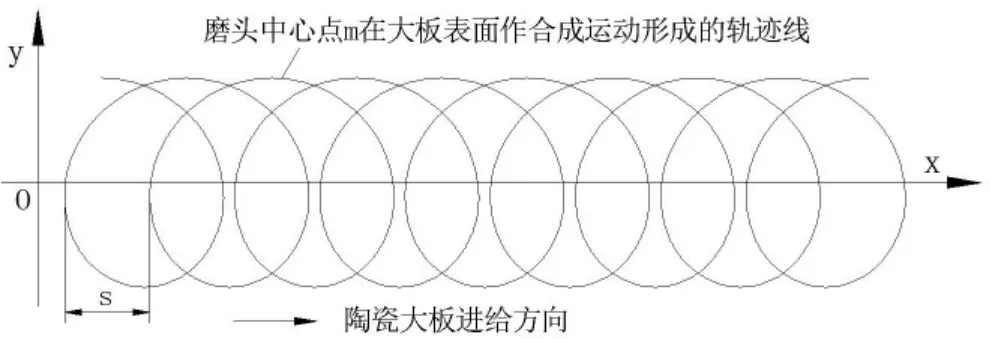
图10 陶瓷大板表面连续研抛轨迹

（2）节距与圆周轨迹旋转速度之间的关系。

节距s与圆周轨迹旋转速度u、圆周轨迹的半径R，这三者之间的匹配关系直接影响着陶瓷大板的加工均匀性。圆周轨迹旋转一周所用的时间为t。

式中：ω——圆周轨迹旋转角速度，（rad/s）

磨头中心点m沿着圆周轨迹旋转一周，陶瓷大板的进给距离为：

将其代入（10）式得：

式中：v——陶瓷大板直线进给速度，（m/min）；

ω——圆周轨迹旋转角速度，（rad/s）；

R——圆周轨迹半径，（mm）；

λ——速度比；

u——圆周轨迹线的圆周线速度，（mm/s）。从（11）式看出，节距s也就是陶瓷大板的进给量，由陶瓷大板的进给速度、圆周轨迹线的圆周线速度、圆周轨迹的半径确定。只要改变其中的一个，就可以改变陶瓷大板的进给量。

（3）最佳节距的确定。

如图11所示，磨头的磨削半径为r，磨块的长度L。磨头旋转一周，磨削区域为一个圆环，圆环中间为空白区域。

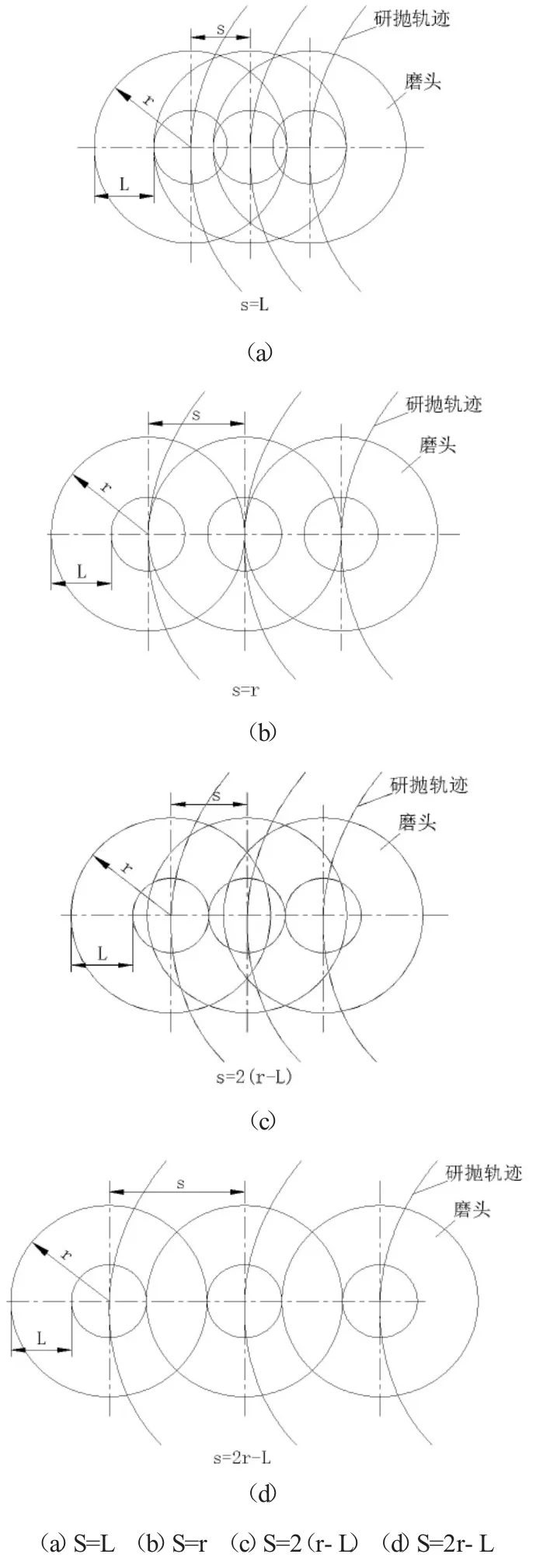
图11 最佳节距

最佳的磨削方式有四种情况，第一种最佳的磨削方式是相邻的两个研磨轨迹，后一个研抛轨迹的磨头磨块长度L磨削的区域能够磨削到前一个研抛轨迹磨头大半个圆环空白区域，如图11（a）。节距S=L。研磨轨迹网纹紧密均匀。

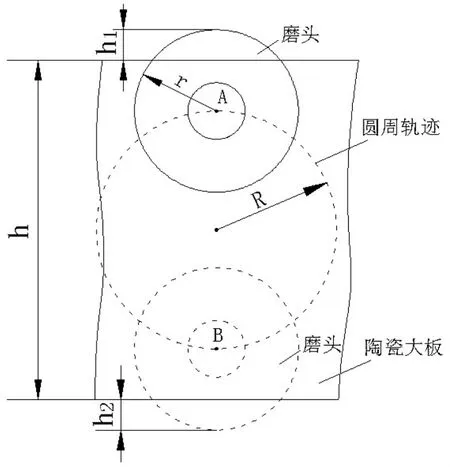
图12 圆周轨迹极限位置

第二种最佳的磨削方式是相邻的两个研磨轨迹，后一个研抛轨迹的磨头磨块长度L磨削的区域能够磨削到前一个研抛轨迹磨头半个圆环空白区域，如图11（b）。节距S=r。研磨轨迹网纹较为紧密均匀。

第三种最佳的磨削方式是相邻的两个研磨轨迹，后一个研抛轨迹的磨头磨块长度L磨削的区域能够磨削到前一个研抛轨迹磨头大半个圆环空白区域，如图11（c）。节距S=2（r-L）。研磨轨迹网纹紧密均匀。

第四种磨削方式是相邻的两个研磨轨迹，后一个研抛轨迹的磨头磨块长度L磨削的区域与前一个研抛轨迹磨头磨块长度L磨削的区域，相互重合。磨头圆环空白区域没有被磨削到。就会出现磨削不均匀的现象。因此，第四种磨削方式是不适合的。

厂家可以根据陶瓷大板的实际情况，选择不同的节距S。

（4）圆周轨迹半径R的确定。

由前面的分析可知，横梁的圆周轨迹是由其两端的曲柄旋转造成的。圆周轨迹的半径R，也就是曲柄旋转的半径。图12中，陶瓷大板的宽度为h，磨头在陶瓷大板边缘处的两个极限位置A、B。磨头到陶瓷大板的极限位置，磨头超越陶瓷边缘位置，也叫越程量。图中h1、h2分为两个极限位置的越程量，而且h1=h2。磨头的半径r。