改进近场动力学方法在圆柱绕流问题中的应用

朱红玉，刘立胜，2，刘齐文，赖 欣

(1.武汉理工大学力学系，湖北 武汉 430070；2.武汉理工大学材料复合新技术国家重点实验室，湖北 武汉 430070)

流体工程问题广泛应用于原油勘探、水文地质学、多孔介质渗流[1]等领域。过去50年,流体力学随着计算机的发展迅速崛起，实验方法较难满足流体真实的运动状态，且效率低、成本高，相比于风洞实验方法，数值模拟方法可以更高效地研究不同因素对流体外流场性能的影响[2]。因此，有效发展数值方法研究流体的运动状态意义重大。

目前描述流体连续介质运动有两种方法[3]：欧拉方法和拉格朗日方法。其中，欧拉方法将物理量表示成与流体粒子空间位置、时间相关的函数；拉格朗日方法跟踪流体粒子，记录物理量与流体粒子空间位置、时间的关系。本文采用拉格朗日方法跟踪流体粒子，对流体的运动状态进行描述[4]。近场动力学方法是基于流体连续介质力学的一种非局域方法，由Silling[5]提出，不同于扩展有限元方法等需额外添加判据，近场动力学方法的流体运动控制方程是积分形式的，没有空间导数，克服了网格依赖性、非物质奇异性、失效准则选取[7]等困难，而近场动力学键理论与经典理论的区别在于有限距离上的键与接触力[8]。

近场动力学方法过去十几年发展迅速，已成功运用于裂纹扩展[9]、热传导[10]、烧蚀[11]等领域。如廖洋等[12]采用近场动力学强度折减法分析了边坡的稳定性问题;Oterkus等[13]采用近场动力学方法，在不引用其他失效准则情况下研究了渗流裂纹构型中的压力场与裂纹的扩散；Katiyar等[14]采用常规态理论研究了微压缩单相对流流体在均匀多孔介质中的流动；Yang等[15]采用浸入边界法研究了流体结构与多相黏性流作用;王瀚霖等[16]提出的预测模型考虑了摩擦阻力与流体的可压缩性对天然气管道压力变化的影响，且通过对比验证了该模型的预测结果较为准确;周学君等[17]将近场动力学中描述流体粒子之间相互作用的本构力引入光滑粒子流体动力学方法中用于处理固壁边界，能够体现真实的边界作用，很好地解决了流体粒子非物理穿透边界问题；Cundall等[18]在研究岩石变形时，考虑粒子流中颗粒间的相互作用，分别表示了颗粒上的法向力和切向力。

基于上述研究，本文在近场动力学方法中“法向键力”的基础上引入“切向键力”，共同描述流体粒子的受力状态，这种方法相比传统的近场动力学键理论方法，能更有效地描述流体粒子间的“切向黏性力”作用，根据均质不可压缩牛顿流体的运动特性，考虑粒子邻域范围内粒子间的相互作用力与压力、黏性力的关系，推导出基于拉格朗日描述的近场动力学形式的流体运动控制方程。采用Fortran语言编程利用该方法计算相应的算例，并与有限体积法的模拟结果进行了对比，从而验证了本文提出的改进近场动力学键理论方法在研究流体问题中的可行性和有效性，促进了近场动力学在流体问题领域中的应用研究。

1 改进近场动力学键理论的计算方法

1. 1 流体本构方程

流体中一点的应力状态由9个分量构成，由矩阵表示流体应力状态P(表示应力矩阵)的张量形式可写为[19]

pij=-pδij+τij

(1)

式中:pij为应力张量(i、j分别取x、y、z);p为压强;δij为克罗内克δ(当i=j时，δij=1;当i≠j时，δij=0);τij为偏应力张量。

(2)

式中:4πa2表示半径为a的球的表面积;pnn为压力积分项;dA为面积微元;pxx、pyy、pzz分别表示x、y、z方向的压应力。

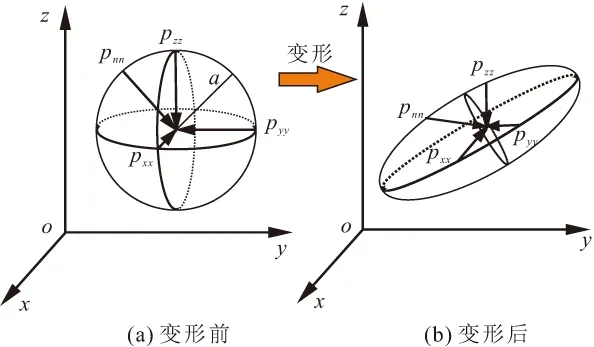
图1 流体元变形前、后压力示意图Fig.1 Diagrams of the pressure of undeformed and deformed fluid element

对于二维流动问题，上述计算公式可转化为

(3)

式中：2πa表示半径为a的二维流体元的周长;dS为弧长微元。

假设平均压强(以下简称为压强)与热力学压强相等，则有：

(4)

当i=j时，式(1)中τij为附加法向应力，表示在流体元上3个法向应力分量偏离平均压强的部分，该应力与流体元的变形率相关，当流体静止时该量消失。

根据Stokes提出的三个假设[19]：①流体应力与变形率成线性关系；②流体是各向同性的，应力与变形率的关系与坐标系的选取无关；③流体静止时，法向应力等于静压强。

可得到牛顿流体的本构关系如下：

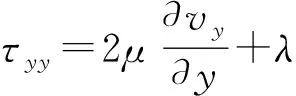
(5)

式中:vx、vy分别表示沿x、y方向的速度;μ为分子黏性系数；λ为第二黏性系数。

μ与λ的关系式为

(6)

则二维流体本构方程可表示为

(7)

式中:σ为应力矩阵;I为单位矩阵;D为变形率张量。

1. 2 法向键力与切向键力的推导

本文基于近场动力学键理论思想[5]，并考虑了粒子邻域δ范围内粒子间的相互影响，考虑粒子间沿键长方向的法向键力作用和沿键切线方向的切向键力作用。在流体运动中，可认为压强与沿键长方向速度分量影响法向键力，沿键切向速度分量影响切向键力[19]。粒子x与邻域范围内粒子x'之间的法向键力和切向键力示意图见图2。

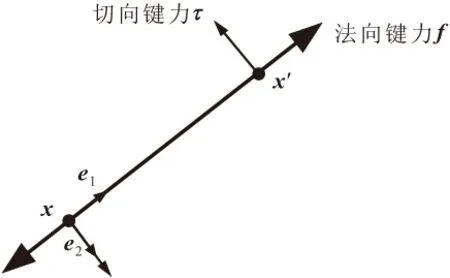
图2 粒子x与领域范围内粒子x'之间的法向键力和切向键力示意图Fig.2 Schematic diagram of normal bonding force and tangential bonding force in peridynamics between particle x and x' in the neighborhood

在粒子邻域范围内，假设粒子x与粒子x'之间的键与x轴夹角为θ，沿键长方向单位矢量为e1，沿键切线方向单位矢量为e2，粒子邻域半径为δ，见图3。其中：

e1=cosθi+sinθj

e2=sinθi-cosθj

(8)

式中：i、j分别表示x、y方向的单位矢量。

图3 粒子键力作用邻域Fig.3 Neighborhood of particles’ bonding force

在邻域范围内粒子x与粒子x'之间的作用力有沿着键方向的法向键力f和垂直于键方向的切向键力τ作用，则基于键理论的近场动力学运动平衡方程[4]为

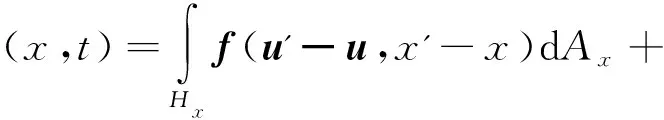
(9)

式中:ρ为粒子的材料密度;u为位移矢量;ü(x,t)为粒子x在t时刻位移的二阶导数，表示加速度矢量;x为粒子x的初始坐标;x′为粒子x′的初始坐标；f为点对相互作用函数;τ为切向作用力。

将公式(9)沿着坐标轴分别分解至x和y方向，则有：

(10)

式中：üx、üy分别表示粒子沿x、y方向的加速度；dAx表示粒子x邻域范围内面积积分微元。

由均质不可压缩牛顿流体Navier-Stokes方程中的动量方程：

(11)

式中:x方向加速度方程中，压力与速度沿x方向变化产生的加速度由法向键力引起，压力与速度沿y方向变化产生的加速度由切向键力引起。

同理，可分析y方向加速度方程。为了区分方向，下面用粒子i代表粒子x，用粒子j代表粒子x′，根据近场动力学思想[10]，则粒子i与粒子j间的“法向键力”可表示为

(12)

式中:p为压力;v为速度矢量，ζij为粒子间相对位置矢量。

同理，粒子i与粒子j间的“切向键力”可表示为

(13)

式中：c1、c2、c3为键参数。

将公式(12)和(13)代入公式(10)中，并沿x方向分解，则x方向的流体运动控制方程为

(14)

采用近场动力学键理论方法分析的某粒子的加速度应与传统方法中粒子加速度的表达式相等[10]，则有：

(15)

推导过程中，法向键力取的速度邻域[20]见图4，切向键力取的速度邻域见图5。

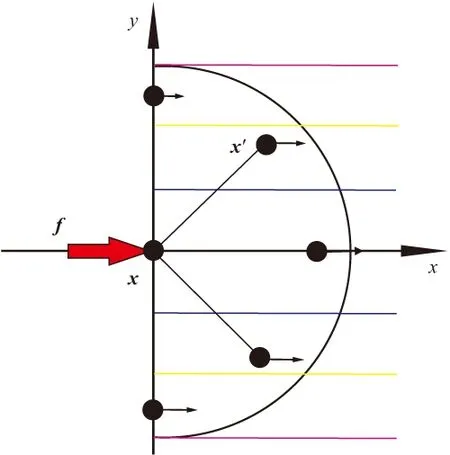
图4 法向键力速度邻域Fig.4 Neighborhood of normal bonding force by velocity effects

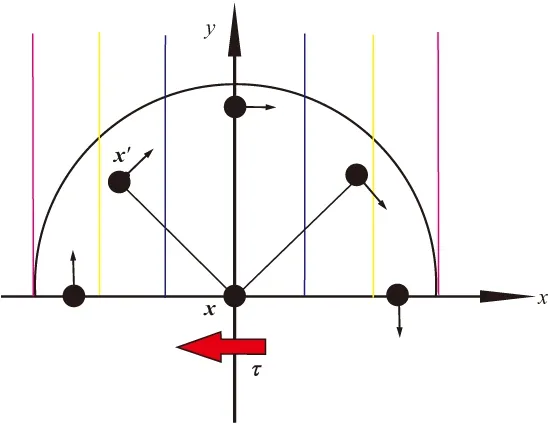
图5 切向键力速度邻域Fig.5 Neighborhood of tangential bonding force by velocity effects

可求得键参数c1、c2、c3为

(16)

将公式(16)代入公式(14),即可得到改进的近场动力学键理论方法的流体运动控制方程。

1. 3 边界条件和初始条件的设置

本文选取无限域圆柱绕流问题进行研究，因此边界条件涉及到圆柱表面和壁面的处理。圆柱表面定义为无滑移壁面条件，边界上流体粒子的速度等于固体粒子的速度，由于本文研究的是静止圆柱，所以在圆柱表面边界Γf上，有：

vxf=0,vyf=0

(17)

式中：vxf、vyf分别表示流体粒子在x、y方向的速度。

壁面边界条件为

vxs=vxf,vys=vyf

(18)

式中：vxs、vys分别表示固体粒子在x、y方向的速度。

公式(18)则表示壁面固体粒子的速度与其相邻流体粒子的速度相同。

速度入口边界条件需要确定来流速度，可以通过分量形式或矢量形式来指定。本文选取流向为x方向，垂直于x方向的逆时针为y方向正方向，则速度入口边界上的速度应为来流速度v0，即

vxf=v0,vyf=0

(19)

出流边界上的零扩散通量条件是指出流边界面上的流动变量均由流场内部变量值外插得出。本文由于求解二维均质不可压缩流体控制方程，因此使用了与来流速度相同的均匀流场对流场做了初始化处理。

2 圆柱绕流问题的计算流程

2. 1 计算流程

根据上述改进的近场动力学键理论方法推导出的流体运动控制方程，可根据速度场计算出压力场和粒子加速度，并对粒子速度、位置进行更新。圆柱绕流问题的计算流程见图6。

图6 圆柱绕流问题的计算流程图Fig.6 Flow chart of flow around a cylinder

2. 2 空间离散与时间积分

改进的近场动力学键理论方法的流体运动控制方程计算的离散格式如下：

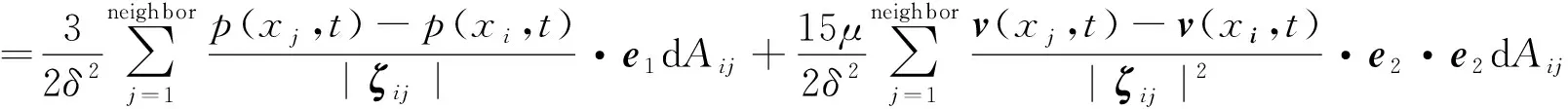
(20)

对于某粒子i，假设其邻域某一粒子为j，则根据方程式(20),可计算得到粒子当前时刻的加速度，再根据Velocity-Verlet积分方法更新粒子速度、位移，从而完成流体状态的更新。

3 算例应用与分析

3. 1 二维圆柱绕流问题的计算模型

本文选取雷诺数约为10，均匀来流的二维圆柱绕流模型，流场的尺寸和边界条件见图7。圆柱直径D为0.01 m，选取计算域宽度为0.05 m，圆柱前方流场和后方流场分别为0.06 m和0.04 m，入口处流入速度vx= 0.001 m/s、vy=0.0 m/s，流场两侧壁处vy=0.0，圆柱壁面处vx=vy=0.0 m/s。流场计算域离散为27 000个粒子，计算时间步长取0.000 25 s，计算时间步为200 000步。计算模型采用Fortran语言编程实现。

图7 流场尺寸和边界条件Fig.7 Geometry and boundary conditions of flow field

3. 2 数值计算结果

本文利用改进的近场动力学键理论方法和有限体积法(商业软件Fluent)模拟计算得到圆柱绕流算例瞬态1.25 s、50 s时在x、y方向的速度分布云图，详见图8至图11。

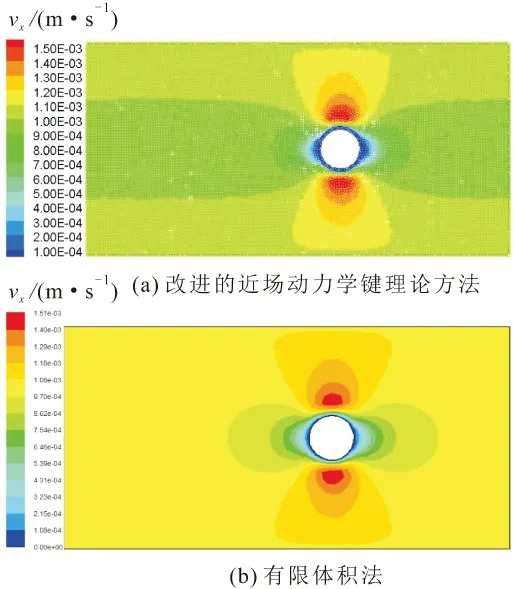
图8 1.25 s时圆柱绕流算例在x方向的速度分布云图Fig.8 X-direction velocity distribution of flow around a cylinder based on the improved bondbased peridynamics and the finite volume method at 1.25 s

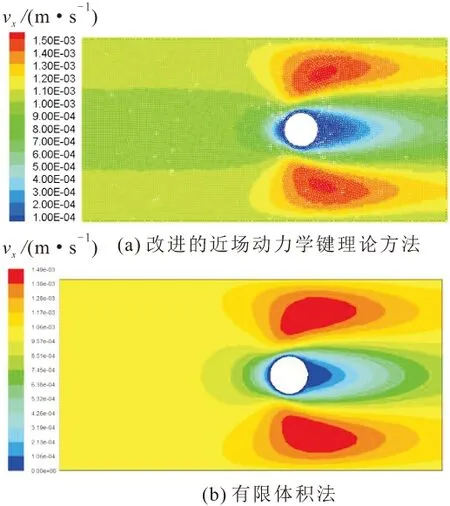
图9 50 s时圆柱绕流算例在x方向的速度分布云图Fig.9 X-direction velocity distribution of flow around a cylinder based on the improved bondbased peridynamics and the finite volume method at 50 s

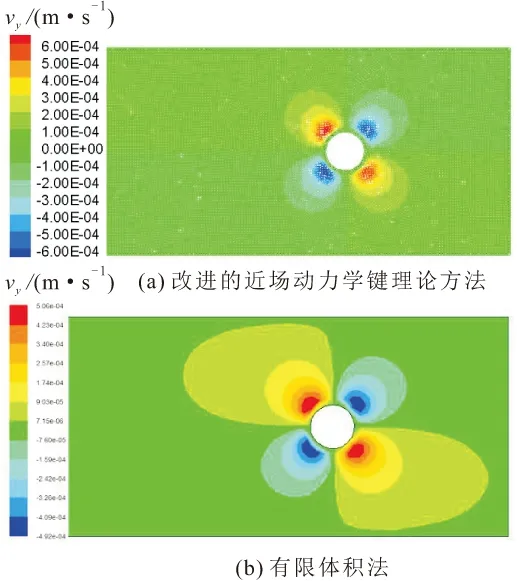
图10 1.25 s时圆柱绕流算例在y方向的速度分布云图Fig.10 Y-direction velocity distribution of flow around a cylinder based on the improved bondbased peridynamics and the finite volume method at 1.25 s

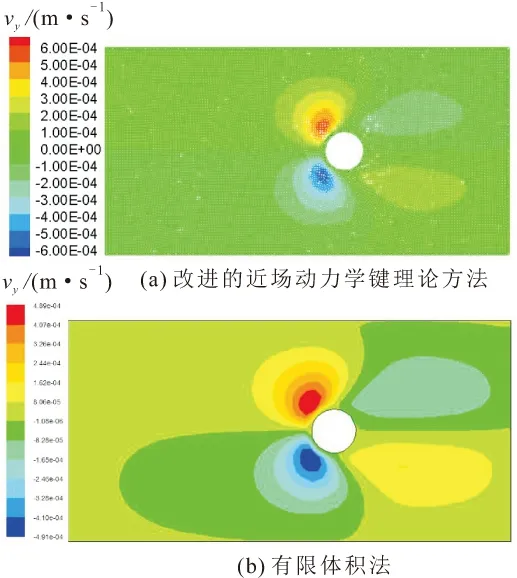
图11 50 s时圆柱绕流算例在y方向的速度分布云图Fig.11 Y-direction velocity distribution of flowaround a cylinder based on the improved bondbased peridynamics and the finite volume method at 50 s

由图8至图11可见，本文提出的改进近场动力学键理论方法可在相同的初始条件、边界条件下初步计算流体的速度场，与有限体积法的模拟结果较为接近，但在某些位置存在一些差异，产生这种差异的原因可能是：圆柱壁面处流体粒子与圆柱的作用，有限体积法对网格的依赖性较强，而改进的近场动力学键理论方法直接考虑了邻域内粒子间的相互作用，且与邻域大小、粒子间距的选取有很大的关系，因而影响了数值模拟计算结果的精度。

当雷诺数为10时，采用本文提出的改进近场动力学键理论方法计算无限域中圆柱绕流算例的耗时大于商业软件Fluent，但本文提出的改进方法与有限体积法的计算结果匹配较好，主要表现为：本文提出的改进近场动力学键理论方法与商业软件Fluent的模拟结果相比，在x方向速度值大小和分布位置相近，终止时刻速度最大值误差约为6.4%，总体分布相似，且分布范围一致；在y方向速度分布结果虽不如x方向的精度高，但总体分布仍相似，且分布范围和趋势一致，终止时刻速度最大值误差约为22.6%。

4 结论与建议

本文在传统近场动力学键理论方法的基础上，提出了一种改进的近场动力学键理论方法，并对给定条件下圆柱绕流问题算例进行了数值模拟分析，得到如下主要结论：

(1) 研究均质不可压缩黏性流体平面运动时，在传统近场动力学键理论方法基础上，考虑了“法向键力”作用，并引入“切向键力”作用，通过键力与流体本构之间的联系，分别推导了“法向键力”与“切向键力”的键参数，并推导出基于拉格朗日描述的近场动力学形式的流体运动控制方程。

(2) 相比传统的近场动力学键理论方法，本文提出的改进方法能够考虑流体粒子间黏性力的影响，初步反映了流场中黏性剪切的作用。采用Fortran语言编程，利用改进的近场动力学键理论方法模拟计算了低雷诺数时无限域圆柱绕流问题算例，并与有限体积法(商业软件Fluent)的模拟结果进行了对比分析，结果表明：本文提出的改进方法与Fluent软件的模拟结果在x、y方向速度场的分布、变化趋势基本一致，且终止时刻速度最大值误差分别为6.4%、22.6%，能够初步实现对给定条件下流体运动的描述，从而验证了本文提出的改进近场动力学键理论方法在流体运动状态捕捉中的可行性，对近场动力学方法在流体方面的应用与探究作出了一定的贡献。在后续研究中可考虑引入圆柱固体材料参数，着手处理流体粒子与固体粒子之间的强耦合作用，分析流场对固体部分的作用，从而为实际工程中圆柱部分材料的强度设计、流场中圆柱构件的排布等提供参考。