Moser-Trudinger不等式及其极值函数的存在性
2018-10-10李嘉禹杨云雁朱晓宝
李嘉禹,杨云雁,朱晓宝
(1.中国科学技术大学 数学科学学院,合肥 230026;2.中国科学院 数学与系统科学研究院,北京 100080; 3.中国人民大学 数学系,北京 100872)
Moser-Trudinger不等式作为临界情形的Sobolev嵌入定理,是由著名数学家Trudinger[1]在1967年首先得到的.设Ω是n中的光滑有界区域,是在范数
(1)
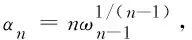
称不等式
∀0<α≤αn
(2)
为Moser-Trudinger不等式.
Carleson等[3]发现了一个令人惊讶的事实:在Ω是单位球的时候,存在函数能达到(2)式中的上确界,即它的极值函数存在,而这个事实对次临界的Sobolev不等式是不对的.随后,Flucher[4]和Lin[5]分别证明了对2维和n维的一般区域,(2)式的极值函数也存在.
论文旨在介绍Moser-Trudinger不等式及其极值函数存在性的相关进展.第一部分,介绍紧黎曼曲面上的Moser-Trudinger不等式及其应用;第二部分,介绍一般维黎曼流形上的Moser-Trudinger不等式;第三部分,介绍一类改进的Moser-Trudinger不等式;最后,介绍带奇异位势的Moser-Trudinger不等式.
1 紧黎曼曲面上的Moser-Trudinger不等式及其应用
由不等式(1)和紧黎曼曲面上的单位分解,可得定理1.
定理1[1]设(Σ,ds2)是紧黎曼曲面,则存在c>0,使得不等式
成立.
由Cauchy不等式,有定理2.

其中:CΣ是只与(Σ,ds2)有关的正的常数.
1.1 预定高斯曲率问题
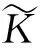
(3)
对(3)式两边在Σ上积分,可得
(4)
因而,可将对方程(3)的求解分为χ(Σ)<0,χ(Σ)=0和χ(Σ)>0这3种情形.下面介绍变分方法和Moser-Trudinger不等式在这3种情形中的应用.Berger[6]通过寻找泛函
(5)

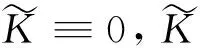
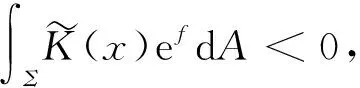

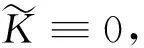
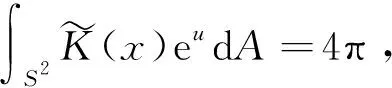
(6)
由定理2知,泛函J(u)是弱下半连续的.为了清楚泛函J(u)是否满足强制性条件,Moser计算了定理1中的最佳常数,证明了定理5.
定理5[2-8]在标准球面(S2,g0)上,成立
和
作为定理5的直接推论,有定理6.
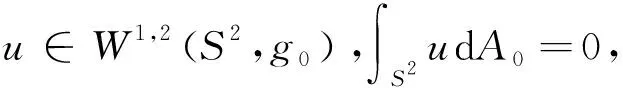
其中:CS2是只与(S2,g0)有关的正的常数.
由定理6(i),泛函J(u)有下界.由定理6(ii)知,泛函J(u)在空间
{u∈W1,2(S2,g0):u(x)=u(-x)a.e.x∈S2}
中满足强制性条件.由经典的变分理论,有定理7.
定理7[8]设K是S2上的光滑函数,满足K(x)=K(-x),∀x∈S2且存在x0∈S2,使得K(x0)>0,则方程(3)有光滑解.
更多的关于Nirenberg问题的研究可参见文献[9-12].
1.2 Kazdan-Warner问题
设(Σ,ds2)是一个紧黎曼曲面,为方便起见,约定它的面积是1.设h(x)是(Σ,ds2)上的光滑函数.Kazdan等[7]问:对h加什么条件,可使得方程
Δu=8π-8πheu
(7)
有解.这个问题被称为Kazdan-Warner问题,它可以看成是Nirenberg问题的推广.当(Σ,ds2)不是球面或实投影平面时,它上面不再有常正曲率的背景度量,因而此时的方程(7)不是预定高斯曲率问题,但它会出现在Chern-Simons Higgs理论中[13-14].
(8)
的临界点.
Ding等首先证明了(8)式中定义的泛函J(u)有下界,这也将S2上的Moser-Trudinger不等式——定理6(i)推广到了一般的紧黎曼曲面上.

其中:CΣ是只与(Σ,ds2)有关的正的常数.
为了证明泛函J(u)有下界,文中考虑了J(u)的扰动泛函
其中:ε>0.
由变分的直接理论,泛函Jε(u)在某个uε处达到它的极小值.现在有两种可能:
(i)uε在W1,2(Σ)中有界;
(ii)uε在W1,2(Σ)中无界.
对于第一种情形,容易验证存在某个u0∈W1,2(Σ),使得泛函J(u)在u0处达到极小.当然,此时u0就是方程(7)的解.
文中主要分析了第二种情形,称为uε爆破.经过细致分析,最终计算出在uε爆破的条件下,有
(9)
其中:A(p)是格林函数展开式中的常数项.接下来,在一个几何条件下构造了一列φε,满足J(φε) 定理9[15]设K是(Σ,g)的高斯曲率,如果 Δlogh(x)>-(8π-2K(x)),∀x∈Σ, 则泛函J(u)可以达到极小,方程(7)可解. 上述方法是在经典的变分理论(满足弱下半连续和强制性条件的泛函,可以在自反的巴拿赫空间中达到它的下确界)的强制性条件不满足,泛函极小化序列爆破的情形下,使用扰动泛函分析出泛函的下确界;然后再构造爆破序列,使得爆破序列上的泛函值小于之前得到的下确界,进而说明爆破不会发生,泛函达到极小,对应的方程可解.该方法被多次应用于求解物理与几何中带临界指标的方程中.参见文献[16-24]. 定理10[25]设K是(Σ,ds2)的高斯曲率,h是Σ上的光滑函数,满足:h≥0,h≢0,如果 Δlogh(x)>-(8π-2K(x)),∀x∈Σ{h(x)=0}, 则泛函J(u)可以达到极小,方程(7)可解. 紧黎曼流形上的Moser-Trudinger不等式是Aubin[26]首先提出, 并由Cherrier[27-28]证明了次临界的情形,最终Fontana[29]计算出了它的最佳常数. 定理11[26-29]设(M,g)是n维紧黎曼流形.对任意的0<α≤αn,成立不等式 (10) 其中:αn是最佳常数,即当α>αn时,不等式(10)不再成立. Li在文献[30-31]中使用变分的方法和爆破分析研究了不等式(10)的极值函数,得到定理12. 定理13[32-35]对任意的0<α≤αn,有 (11) 其中:αn是最佳常数. 关于Moser-Trudinger不等式(11)的极值函数,有定理14. 定理14[36-37](i) 当n=2时,存在某个α0>0,使得当α∈(α0,α2]时,Moser-Trudinger不等式(11)的极值函数存在;当α>0很小时,Moser-Trudinger不等式(11)的极值函数不存在. (ii) 当n≥3时,Moser-Trudinger不等式(11)的极值函数存在. 定理15[38]对任意的0<α≤αn,有 (12) 其中:αn是最佳常数. 在一般的n维完备非紧的黎曼流形(M,g)上,记 定理16[39]如果(M,g)的Ricci曲率有下界,单射半径有一致的正下界.那么对任意的0<α<αn,存在某个τ>0,使得不等式 (13) 成立,其中:αn是最佳常数. 当α=αn时,Moser-Trudinger不等式(13)是否成立,目前并不知道.该不等式的极值函数问题目前也不清楚. 设D是2中的有界区域,记有定理17. 定理17[40](i) 对任意的0≤α<λ1(D),有 (ii) 对任意的α>λ1(D),有 Yang[41]使用变分方法和爆破分析,将定理17分别推广到了高维和紧黎曼曲面的情形,有定理18. 定理18[41]设Ω是n中的光滑有界区域,n≥3.记 有 (i) 对任意的0≤α<λ1(Ω),有 (14) (ii) 对任意的α>λ1(Ω),有 (iii) Moser-Trudinger不等式(14)的极值函数存在. 定理19[42]设(Σ,ds2)是一个紧黎曼曲面.记 有 (i) 对任意的0≤α<λ1(Σ),有 (15) (ii) 对任意的α>λ1(Σ),有 (iii) 当α>0很小时,Moser-Trudinger不等式(15)的极值函数存在. 设B是2中的单位圆盘,H是在范数 下的完备化.使用变分的方法和爆破分析,Wang等[43]证明了定理20. 定理20[43]不等式 的极值函数存在. 定理21[44]对任意的0≤α<λ1(B),不等式 的极值函数存在. Tintarev[45]考虑了一类更广的Moser-Trudinger不等式,证明了定理22. 定理22[45]不等式 (16) 成立,其中:V(x)>0是一类函数,它包含了定理20和21中的函数作为特例(具体见原文). 当V(x)≡α,0≤α<λ1(D)时,有定理23. 定理23[46]对任意的0≤α<λ1(D),不等式 (17) 的极值函数存在. 定理24[46]当0≤α<λl+1(D)时,不等式 的极值函数存在. 在紧黎曼曲面上,也有类似结果,有兴趣的读者可参见原文. 假设0∈Ω,Adimurthi等[47-48]将Moser-Trudinger不等式(2)和(11)分别推广到定理25、26带奇异位势的情形. 定理25[47]设0<β<1,对任意的0<α≤αn(1-β),有 (18) 定理26[48]设0<β<1, 对任意的0<α≤αn(1-β),有 (19) 定理27[49]当n=2时,Moser-Trudinger不等式(18)的极值函数存在. 定理28[50]Moser-Trudinger不等式(19)的极值函数存在. 至于n≥3时,Moser-Trudinger不等式(18)的极值函数是否存在目前尚不清楚.最近,作者用变分的方法和爆破分析得到了一类改进的带奇异位势的Moser-Trudinger不等式. 定理29[51]对任意的0<β<1和任意的0≤α<λ1(D),不等式 的极值函数存在. 定理30[51]对任意的0<β<1和任意的0≤α<λl+1(D),不等式 的极值函数存在.2 一般维黎曼流形上的Moser-Trudinger不等式
2.1 紧黎曼流形上的Moser-Trudinger不等式
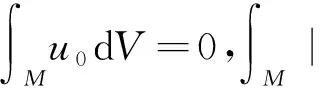
2.2 完备非紧黎曼流形上的Moser-Trudinger不等式
3 一类改进的Moser-Trudinger不等式
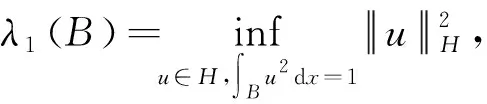
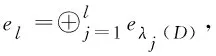
4 带奇异位势的Moser-Trudinger不等式
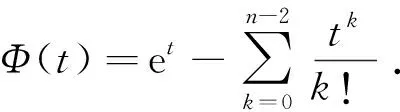
猜你喜欢
杂志排行
安徽大学学报(自然科学版)的其它文章
- 多细胞生物自噬的分子机制和生理功能
- 一类时滞不确定系统的有限时间 非脆弱L2-L∞滤波器设计
- Linear (optimal) complexity direct full-wave solution of full-package problems involving over 10 million unknowns on a single CPU core
- The effect of Unruh effect for quantum-memory-assisted entropic uncertainty relation
- 不确定信息环境下多属性决策方法的研究进展
- 肾脏纤维化的细胞和分子机制研究进展
