汽轮机湿蒸汽区抽汽焓计算模型研究

张 勇， 贾昌盛

(陕西科技大学 机电工程学院， 西安 710000)

大型汽轮机组低压缸蒸汽膨胀到末级或末几级时，一般会进入湿蒸汽区，由于缺乏在线测量湿度的有效方法，无法直接得到湿蒸汽焓。此时，湿蒸汽压力和温度不再是独立参数，蒸汽焓也不能由蒸汽图表查得。

目前，在常规机组性能计算中，对湿蒸汽焓的计算，通常采用ASME PTC6A—1982中推荐的能量平衡法和曲线外推法两种方法。能量平衡法是先假定排汽焓，利用热量、物质平衡方程及汽轮机功率方程，对回热系统进行热平衡计算，得到相应湿蒸汽区抽汽焓，反复迭代直至前后两个抽汽焓偏差满足精度要求。曲线外推法是将机组过热区的热力过程线平滑外推至湿蒸汽区，得到湿蒸汽区的抽汽焓。而对于大型汽轮机组，应用以上两种方案均存

在困难：能量平衡法无法确定多个湿蒸汽区抽汽点焓；曲线外推法由于抽汽拟合点较少，汽轮机过程线外推至湿蒸汽区时焓的精度较差。

针对以上问题，笔者提出了一种基于级内损失理论的湿蒸汽区抽汽焓的近似计算模型，为汽轮机湿蒸汽区焓的计算提供依据。

1 计算模型

蒸汽在汽轮机内膨胀过程中，存在喷嘴损失、动叶损失、叶高损失、叶轮摩擦损失、部分进汽损失、漏汽损失、扇形损失、排汽损失、湿汽损失等多种级内损失，级的理想能量不能全部转化为有效功。考虑各种损失后，低压缸实际热力过程线见图1。

h0—低压缸进口处蒸汽焓，kJ/kg；p0—低压缸进口处蒸汽压力，MPa；pc—湿蒸汽区抽汽压力，MPa；hc—湿蒸汽区抽汽焓，kJ/kg；hct—低压缸进口蒸汽等熵膨胀到湿蒸汽区抽汽压力下的理想焓，kJ/kg。

图1 蒸汽在低压缸内膨胀的热力过程线

根据级的相对内效率公式可知，无论余速是否被下级利用，本级的有效比焓降不变[1]。结合级内损失的理论可知，当汽轮机组的结构参数确定且保持不变时，除湿汽损失和余速损失外的其他损失占理想焓降的比例不变[2-3]。

hc=hct+a(h0-hct)+hx

(1)

式中：a为除湿汽损失及余速损失外的其他损失占理想焓降的比例；hx为湿蒸汽湿汽损失，kJ/kg。

1.1 a的求解

当汽轮机系统变工况运行时，由于进汽参数的变化，低压缸工作级的前后压力比、比焓降、反动度均会有明显的变化[4]。工作级的喷嘴损失、动叶损失也将发生变化。因此由级内损失理论公式可得[5]：

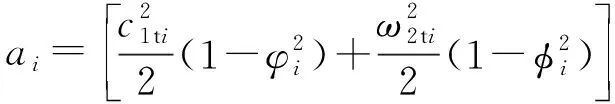
(2)

式中：下标i表示低压缸第i级；φ为喷嘴速度系数；φ为动叶速度系数；Δht为级的理想焓降，kJ/kg；c1t为喷嘴理想出口速度，m/s；ω2t为动叶出口气流的理想相对速度，m/s；m为除余速损失、湿汽损失、动叶损失、喷嘴损失外的其他损失占级的理想焓降的百分比。

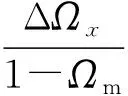
(3)

式中：ΔΩx为速度比变化引起的反动度变化；Ωm设计工况下的反动度；Δxa为速度比的变化；xa为设计工况下的速度比。

在喷嘴和动叶的叶型确定后，喷嘴和动叶的速度系数基本确定。近似认为喷嘴和动叶的速度系数相等[7]，喷嘴损失、动叶损失与级的反动度的关系式为：

(4)

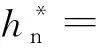
(5)

动叶进出口速度关系式为：

ω12=c12+u2-2c1ucosα1

(6)

式中：w1、c1、u分别为喷嘴出口相对速度、喷嘴出口绝对速度、轮周速度，m/s；α1为喷嘴出口速度方向角，rad。

联立式(2)、式(3)可化为：

ai= (1-φi2){1+[1-(Ωm-0.4(1-Ωm)

(7)

式中：xi为低压缸第i级速度比。

在变工况时，近似认为低压缸结构参数、速度系数保持不变。由速度比与理想焓降的关系，将式(4)中速度比的多项式替换成理想焓降的多项式[8]，则式(7)可写成只与理想焓降有关的多项式，并推广到低压缸湿蒸汽区：

a=t1+t2(t3-Δhi)(Δhi-t4)2

(8)

式中：t1、t2、t3、t4是常数，其数值可以通过若干已知工况，利用最小二乘法拟合得到。

1.2 级内湿汽损失的计算

利用湿蒸汽干度计算公式(9)，并结合级内湿汽损失的经验公式(10)[9-10]，联立可得式(11)：

(9)

hx′=(1-(1+x′)/2)Δh′

(10)

(11)

式中：hci′为第i次计算得到的湿蒸汽焓，kJ/kg；hcq为不计湿汽损失、余速损失的级内湿蒸汽焓，kJ/kg；x′为焓为hcq和湿蒸汽区抽汽压力下的干度；hg为湿蒸汽区抽汽压力下饱和蒸汽焓，kJ/kg；hl湿蒸汽区抽汽压力下饱和水焓，kJ/kg；Δh′ 为未计湿汽损失级的有效比焓降，kJ/kg；hx′为在干度为x′ 时计算的湿汽损失，kJ/kg。

当hcqhc时，由式(9)计算得到的x′ 大于hc对应的湿蒸汽干度x，同样代入式(10)计算得出的级内湿汽损失小于hc对应的湿汽损失，由式(11)计算得出的hci′小于hc。

利用式hcq=hct+a(h0-hct)，计算得出hcq；代入式(11)求得湿蒸汽区抽汽焓初值hc0′；再由式(11)计算得出的新的湿蒸汽区抽汽焓初值hc1′。迭代计算直至前后两次计算的焓绝对误差满足精度要求时，近似认为计算得到的抽汽焓为实际湿蒸汽区抽汽焓，即hc=hci′。

设Δhd为湿蒸汽区抽汽焓值迭代允许的误差，具体计算流程见图2。

图2 湿蒸汽区抽汽焓值计算流程图

1.3 a计算误差的影响

在近似认为低压缸结构参数、速度系数在变工况下保持不变的前提下，通过已知工况拟合得到的多项式计算求得a，其值存在一定的计算误差。令hcq=hc，根据小偏差原理[11]，则式(11)可转化为：

(12)

对式(12)进行计算可知，δa约为0.01，对计算结果影响很小。

2 结果及分析

在设计工况下，根据设计数据，利用式(1)及hx=(1-(1+x)/2)Δh求取a(见图3)，其中x取设计工况下湿蒸汽干度。

图3 a随低压缸进汽至湿蒸汽抽汽点理想焓降的变化

在已知a及低压缸进汽至湿蒸汽抽汽点理想焓降后，利用最小二乘法求取t1、t2、t3、t4，结果见表1。

表1 不同机组的t1、t2、t3、t4

取Δhd=0.01，利用所提出的计算模型对不同厂家、不同工况下300 MW机组湿蒸汽区抽汽焓进行计算，结果见表2～表4。

表2 东汽300 MW机组第八级抽汽(湿蒸汽)焓计算值与设计值对比

表3 哈汽300 MW机组第八级抽汽(湿蒸汽)焓计算值与设计值对比

表3(续)

表4 北重300MW机组第七级抽汽(湿蒸汽)焓计算值与设计值对比

由表2～表4可知：根据设计数据，由所提出的湿蒸汽区抽汽焓计算模型，计算得到的结果精度可以满足工程要求。

对于不同厂家的汽轮机组，经计算，东汽300 MW机组得到的湿蒸汽区抽汽焓最大相对误差为0.086%，最大误差为2.26 kJ/kg；北重300 MW机组，得到的湿蒸汽区抽汽焓最大相对误差为0.147%，最大误差为3.36 kJ/kg；哈汽300 MW机组，得到的湿蒸汽区抽汽焓最大相对误差为0.085%，最大误差为2.12 kJ/kg。

综上分析可知：该计算模型在机组工况变化时，湿蒸汽区抽汽焓计算值仍保持较高的计算精度，且对不同厂家的300 MW机组均具有良好的适用性。虽然进行了迭代计算，但迭代次数小于3次。

3 结语

笔者基于级内损失理论，建立湿蒸汽区抽汽焓的计算模型：

(1) 利用该计算模型，分别对不同厂家机组的多种工况进行了湿蒸汽区抽汽焓的计算，并与相应工况下的设计值进行对比，证明该方法具有良好的精度。

(2) 通过小偏差理论的分析，证明该模型中不计湿汽损失和余速损失的其他损失占比对最终计算结果影响较小。

(3) 该模型供热抽汽工况时，湿蒸汽区抽汽焓普遍存在较大误差。

(4) 虽然该计算模型存在迭代计算，但迭代次数基本为2～3次，利用编程容易实现计算。