多角度计算圆锥摆弹力的冲量

王 云 张 剑 牛志松

(安徽省滁州中学,安徽 滁州 239000)

图1

例题.如图1是内壁光滑,半顶角为θ的圆锥,离锥顶高h的水平面内一个质量为m的小球做匀速圆周运动.求小球从A到B经过半个周期锥面弹力的冲量大小.

1 模型及考点赏析

本题是关于圆锥摆经典题型.涉及的考点有向心力、冲量、动量定理、平行四边形定则等.物理情境考查学生的空间想象能力,需要利用降维思想把三维降成二维,运算过程考查数学方法解决物理问题能力.由于圆锥摆的弹力是变力,解题的突破口可以选择动量定理,角动量定理等,同时利用微元思想化变为恒.

2 解题方法

方法1：利用动量定理求变力的冲量.

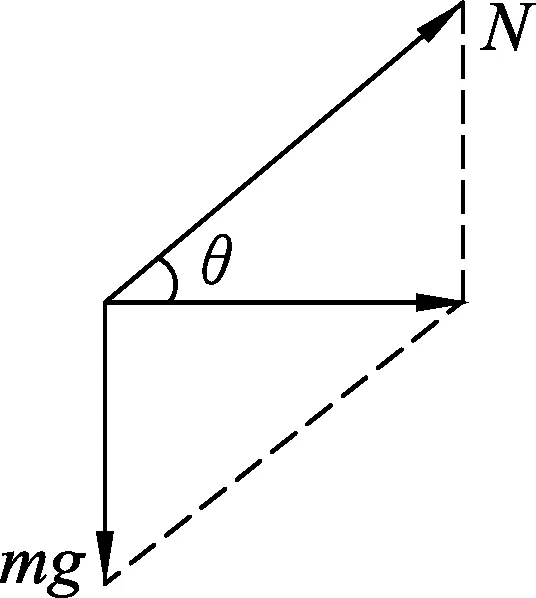
图2

解析： 如图2重力和弹力的合外力提供小球的向心力，有

mgcotθ=mω2htanθ.

(1)

解得

(2)

小球从A到B弹力在竖直方向的冲量为

(3)

弹力在水平方向的冲量由动量定理有

(4)

弹力的冲量为

(5)

评析： 利用动量定理是求解变力冲量的常用方法,同时把力、冲量利用平行四边形定则进行分解与合成达到化繁为简的效果.

方法2： 圆形矢量结合多边形定则,化矢量运算为平面几何运算.

把A到B的时间等分为n(n→∞)等份,每等份时间为

(1)

如图3是各点弹力在水平方向分力,如图4利用多边形定则把n个微元冲量ΔIx=mgcotθΔt矢量首尾相连,构建为半径R的半圆且有

πR=nmgcotθΔt.

(2)

所以弹力在水平方向的冲量为

(3)

弹力在竖直方向的冲量、合冲量同上.

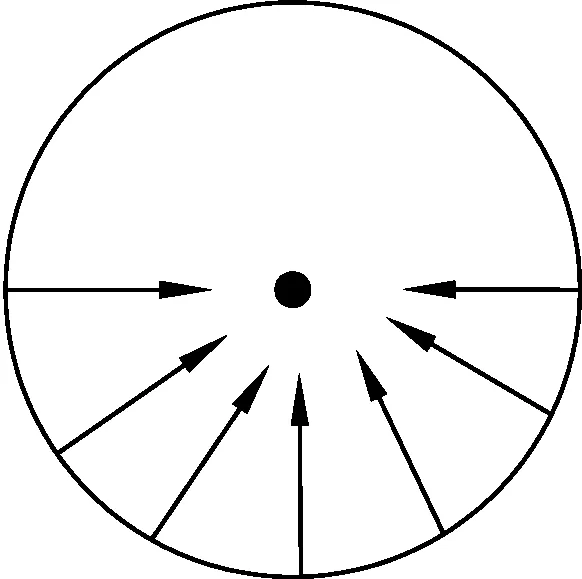
图3

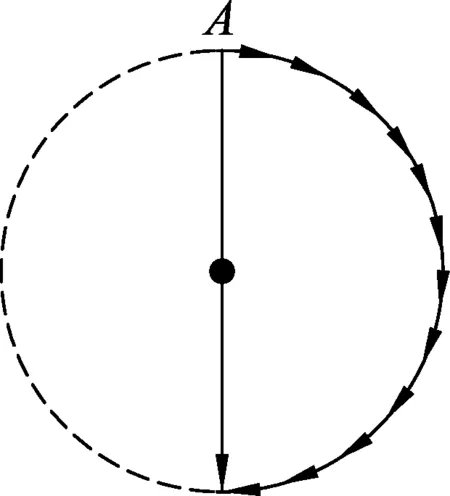
图4

评析： 通过多边形定则化隐形的冲量为显性的平面几何,利用此方法可以求解任意一段时间弹力在水平方向的冲量.概念较前面的动量定理更进一步,但学生更容易理解.

图5

方法3： 利用微元思想、积分方法求解.

设圆锥摆的轨道半径为r,角速度为ω,如图5所示,根据对称性Iy=0,x方向利用微积分求解.

dIx=mrω2sinβdt=mrωsinβdβ.

(1)

两边积分得

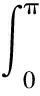
(2)

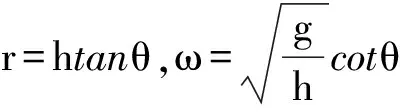
(3)

弹力在竖直方向的冲量、合冲量同上.

评析： 利用微元和积分方法是竞赛问题比较常用、成熟的解题方法,关键选择恰当的微元构建微分方程,统一积分变量后确定积分变量的下限和上限.微元思想、积分方法是理解模型本质、提升科学素养的绝佳机会.

方法4： 利用冲量和冲量矩的关系、角动量定理求解.

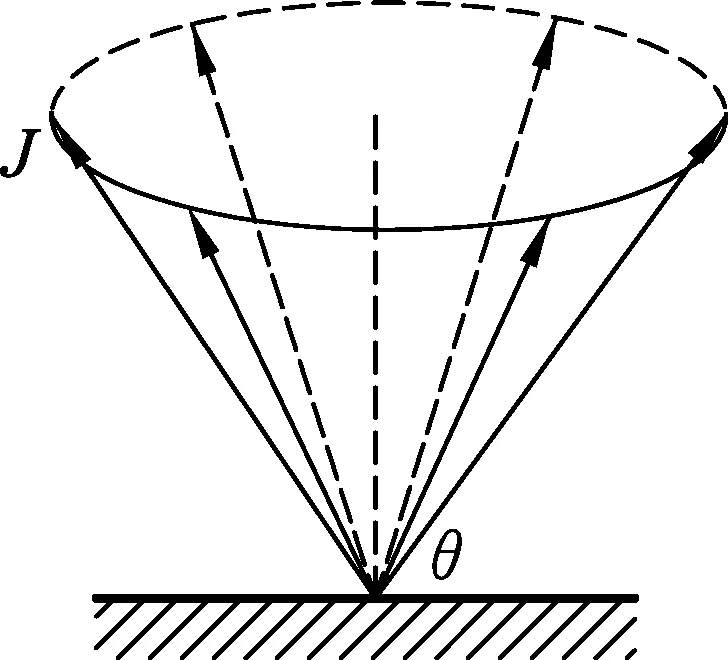
图6

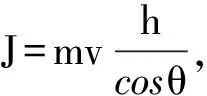
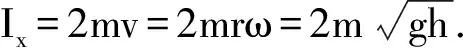
弹力在竖直方向的冲量、合冲量同上.

评析： 从角动量角度分析使学生对模型的本质换个角度去理解,从不同角度研究模型遵循的物理规律便于构建完整、立体的模型情境,同时寻找不同角度、不同方法、不同理论规律间的千丝万缕联系、共性和个性.由于小球在竖直方向满足角动量守恒,以此为出发点自主招生和竞赛有大量的经典试题.

3 基于竖直方向角动量守恒的发散

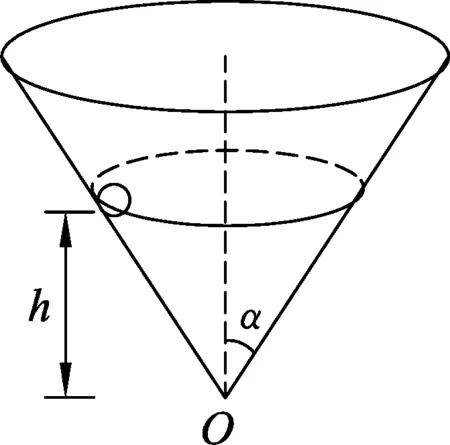
图7

例题.如图7在半顶角为α的圆锥面内壁离锥顶h高处以一定初速度沿内壁水平射出一质量为m的小球,设锥面内壁是光滑的.(1) 为使小球在h处的水平面上做匀速圆周运动,则初速v0为多少?(2) 若初速v1=2v0,求小球在运动过程中的最大高度.

解析： (1) 重力和弹力的合外力提供小球的向心力，有

(1)

解得

(2)

(2) 设小球在运动过程中距O点最大高度为(h+x),在最高点小球只有水平方向速度，由机械能守恒得

(3)

竖直方向角动量守恒,且由前面的推导有Jz=Jsinθ=mvhtanθ，则

mv1htanα=mv(h+x)tanα.

(4)

合并(3)、(4)式得

2gx3+(4gh-v12)x2-2h(v12-gh)x=0.

(5)

可见x=0是一个合理解,代表起点,也是小球能达到的最低高度,消去x后构建方程

2gx2+(4gh-v12)x-2h(v12-gh)=0.

(6)

解得

(7)

由于小球最低点x=0,负解舍去,代入v1=2v0可得

(8)

评析： 简单的模型蕴含丰富的物理信息和规律,在恰当的物理情境里可以自由发散,本题的关键依托于前面的圆锥摆弹力的冲量分析发现小球的重力、弹力都在竖直平面内,所以小球在竖直方向满足角动量守恒,利用守恒思想分析复杂的运动有它得天独厚的优越性.同时依托于本题可以把圆锥面发散为球面等,如2013年第30届全国中学生物理竞赛复赛第1题.

总结： 物理问题源自生活和实践,需要对实际问题抓住主要矛盾,进行合理的模型化处理,把握物理模型的科学本质和关键,进而利用数学方法及进行严格的逻辑推理,所以物理问题分析的一般思路实际问题模型化,物理问题数学化,数学结果物理化.高考、自主招生、竞赛对同一模型的能力要求虽然不一样,但基本遵循分层学习的原则,由理想到实际,由简单到综合,思维体系一脉相承.