圆柱状透镜的趣味实验原理分析
2018-10-09廖永容杨晓梅
廖永容 杨晓梅 肖 瑜
(宁夏大学物理与电子电气工程学院,宁夏 银川 750021)
本文从生活中一种常见的光现象出发,设计了透过装有饱和食盐水的圆柱形塑料水杯观察白色纸片上“单词”的变化情况的小实验,测量了纸片上的“单词变身”时白色纸片、观察者和圆柱形水杯杯壁之间的多组位置关系.并根据厚透镜的物像公式和基点计算出了圆柱透镜垂直于轴方向截面的主点、节点与圆心O3点重合,通过透镜物像公式从理论上计算出了半径为7cm折射率为1.5的圆柱形透镜的成像范围,分析了所成的像的变化特点.通过分析实验数据发现,实验观察到的像的变化特点、物与杯壁之间的位置关系和观察者与杯壁之间的位置关系符合理论分析的成像范围和成像特点.运用实验数据的真实性和理论探究的合理性,验证了单词“变身”实验现象的光学原理.此外,实验还进一步分析论证了在杯子中换密度不同的液体(清水、饱和糖水等)时由于折射率相差不大,所以圆柱透镜所成的像的变化特点和成像范围差异不大.
1 现象描述
实验器材如表1所示.

表1 观察光现象的自组器材
实验步骤1:将白色纸片贴于支架上,把塑料杯放在支架的正前方,观察者于实验台前透过塑料杯平视前方调整纸片和塑料杯的位置,使字母和玻璃杯的几何中心与观察者的视线位于同一条直线上,如图1所示.

图1 加水前的英文单词

图2 加水后的英文单词
实验步骤2:向塑料杯中加饱和食盐水,水的高度高过纸片即可,观察者于实验台前透过塑料杯平视前方以同样的方法观察,发现单词由now变成了won,且被放大了,此时纸片与杯壁之间的距离为8 cm,眼睛与杯壁之间的水平距离为16.2 cm,如图2所示.
实验步骤3:保持字母与塑料杯的几何中心位于同一条直线上,将纸片移动到距离杯壁10.5 cm的地方,发现单词由now变成了won,大小几乎不变,此时眼睛与杯壁之间的水平距离为11 cm.将纸片移动到距离杯壁20 cm的地方,发现单词由now变成了won且缩小了,此时眼睛与杯壁之间的水平距离为7.5 cm.将纸片移动到距离杯壁5.5 cm左右的地方,观察者在任何位置都看不清单词了,当将纸片移动到距离杯壁更近的位置时可以观察到一个清晰放大的单词now.
2 原理分析
透镜的形状是圆柱体或透镜的表面是圆柱面的一部分,这种透镜就叫做圆柱透镜.对于任意一块处于空气中的圆柱形透镜,圆柱体的对称轴就是圆柱透镜的轴,分析时取圆柱体垂直于对称轴的一个截面,该截面是一个以O为圆心,半径为R的圆面.根据高斯基点理论,求出处于空气中的半径为R,折射率为n的圆面的焦距和主点的位置.
假设光从左向右入射,由于r1=R,r2=-R,δ=2R,根据公式
(1)
可以得到圆面的像方焦距为
(2)
结合主点与顶点间距离的公式
(3)
和
(4)
可得p=R,p′=-R.
结果表明圆柱透镜的物方主点H在顶点O1的右边R处,而像方主点H′在顶点O2的左边R处,显然两主点重合且通过圆心O,如图3所示.

图3 主点、节点与圆心O重合
系统的节点是角放大率为γ=1的一对共轭光线与主轴的交点.设物方节点K到物方焦点F的距离为xK,像方节点K′到像方焦点F′的距离为xK′,根据平面节点定义,若将这对节点看作一对特殊的共轭物像点,则xK和xK′分别可视为相应的物距和像距.根据公式
(5)
可得xK=-f,xK′=-f′.
根据圆面的对称性知f=-f′结合(2)式得出
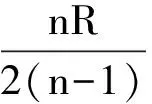
由此可知圆柱透镜垂直于轴截面的主点、节点和圆心3点重合,即任意垂直于圆柱透镜的轴且过截面圆心O的光线方向不发生改变.
空气的折射率为1,饱和食盐水的折射率为n(n=1.5),实验所用透明塑料杯的折射率为1.52.由于塑料杯的折射率与水的折射率只相差0.02,且杯壁厚度0.8 mm与杯子的直径7 cm相比太小,光线在水中走的路程远大于在杯壁中走过的路程.此外,曲面塑料杯壁在很小的范围内可近似的看做平行塑料板,对光线只产生平移作用.所以分析时可以忽略塑料杯与饱和食盐水折射率不同的影响(其实即使考虑其影响,结论也还是一样).
在向杯中注满饱和食盐水后,可将杯和饱和食盐水整体看作一个底面半径为3.5 cm,折射率均匀且大小为1.5的圆柱透镜.对置于空气中的半径为R=3.5 cm的圆柱透镜,同样取垂直于轴方向的截面分析,F和F′分别为物方焦点和像方焦点,根据(6)式可得出该截面的物方焦距和像方焦距分别为f=-5.25 cm,f′=5.25 cm.

图4 物AB反向缩小
当s=2f,即s=-10.5时,s′=10.5,物AB发出的光经圆柱透镜两次折射后成倒立等大的实像A′B′,如图5所示.
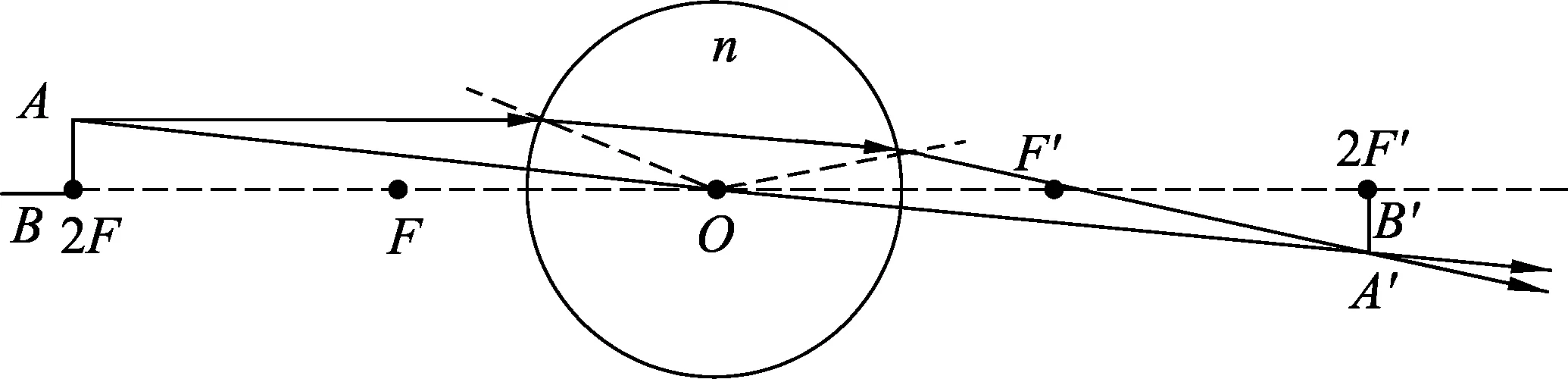
图5 物AB反向等大
当2f

图6 物AB反向放大
当s=f,即s=-5.25时,s′=+∞,物AB发出的光经圆柱透镜两次折射后光线平行射出不成像,如图7所示.

图7 物距等于物方焦距时不成像
当f 图8 物距小于物方焦距时成虚像 物距像距像的性质放大或缩小倒立或正立实像或虚像 s<2f(s<-10.5)f′ 人眼能够看见物体,是因为照射在物体上的光线反射到了人眼中,由物体反射的光线经过圆柱透镜后会在特定的位置汇聚成像,当人眼在光线汇聚的位置附近透过圆柱透镜观察时便能看见像了.通过以上计算可知当物体在O1点左侧的距离发生变化时,像的性质也随之发生变化,下面将圆柱透镜垂直于轴方向截面的成像规律进行总结并做成图表形式,具体如表2. 本实验还另外设计了两种情况:采用密度不同的液体(清水与饱和白糖水)以探究这种圆柱状透镜的成像规律是否会受到杯中液体的密度不同的影响.理论分析:实验时在塑料杯中换不同密度的液体相当于改变透镜的折射率,选用折射率为1.33的水和折射率为1.4的饱和白糖水进行验证,计算得出使用清水和饱和白糖水与使用饱和食盐水时,若取物距相同且成像性质相同的位置,则像距的之差约在1.75~3.6 cm之间.然后用实验验证:用清水和饱和白糖水进行实验观察得到的像的变化特点、物与塑料杯壁之间的位置关系和观察者与塑料杯壁之间的位置关系差异不大,由此再次验证了理论计算的合理性. 物理教学的目的是不仅要学生在学习物理知识的过程中逐渐形成的正确价值观、必备品格和关键能力,更要学生在经历与科学家们探索科学知识相似的过程中,培养学生对科学知识的热爱,探索科学知识的精神.通过本次对装有饱和食盐水的水杯圆柱透镜的成像规律分析,希望鼓励学生对生活中常见的现象和问题能勇于探索,勤于实践,以提高学生的自主创新意识,发展学生的自主学习能力和独立研究能力.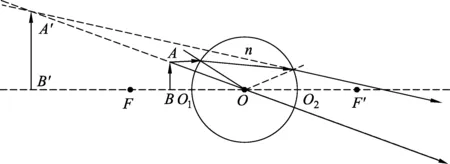

3 实验拓展
4 结束语
