欠自由度假肢对目标定位的实现

2018-10-09吕学义

机电工程技术 2018年9期

关键词：权值坐标系神经元

吕学义，高波

（山东科技大学，山东青岛 266590）

1 欠自由度假肢的定位方法

1.1 定位方法简介

要想让假肢抓取到目标，必须要先得到目标物体的位姿矩阵。本文作者提出的定位方法通过两个姿态传感器和一个激光测距仪获取到了目标的位姿矩阵。其中，姿态传感器用于检测者头部的姿态，激光测距仪用于确认目标。

1.2 硬件的安装位置

两个姿态传感器分别安装在假肢和使用者的头部上；激光测距仪安置在左耳处。

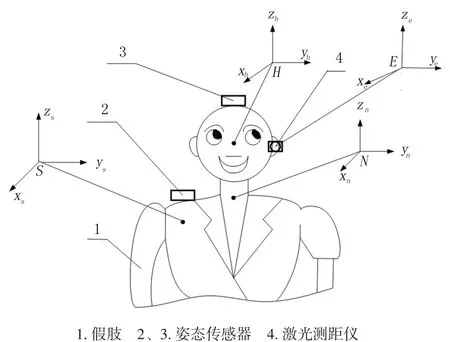
图1 传感器安装示意图

1.3 定位方法的原理

如图2所示，S坐标系是基础坐标系；N坐标系是颈部中心坐标系；H坐标系是头部中心坐标系；E坐标系是测距坐标系；记某坐标系i绕其x轴转动的角度为αi，绕其y轴转动的角度记为 βi，绕其z轴转动的角度记为γi；记H坐标系相对于N坐标系的描述为。

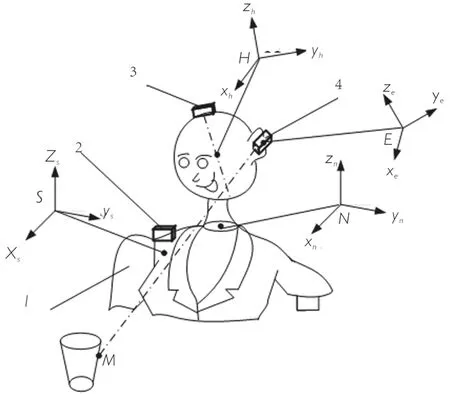
图2 目标物体位姿矩阵获取示意图

N坐标的原点在S坐标系中的描述是(xs,ys,zs)。使用者头部上下转动等价于N坐标系绕S坐标系的y轴转动βs角度。因此，为：

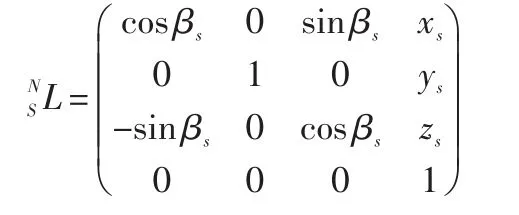
H坐标系的原点在N坐标系中的描述是（0，0，zn），各轴的方位与N坐标系的各轴的方位一致。使用者头部左右转动相当于H坐标系绕N坐标系的Z轴旋转γn。因此，为：

E坐标系的坐标原点在H坐标系里的描述是（0，yn，0），其x轴的方向与激光束的方位重合，其y轴的方向与H坐标的y轴方向重合，其z轴的方位与H坐标系的z轴有个固定的角度βh。因此，为：

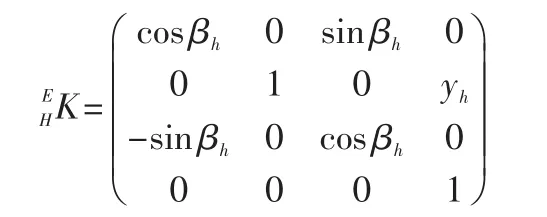
激光测距仪测得的距离用d表示，记：M=[d，0，0，1]。

通过下式即可得到目标的位置P：

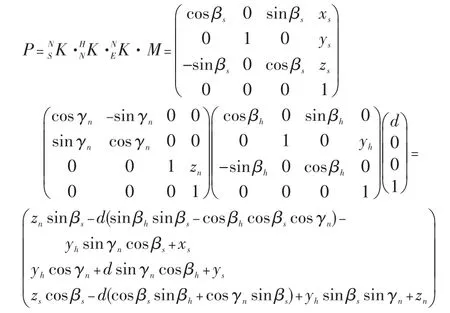
2 定位方法的误差校正

前文所述定位方法的精度受以下两个方面的因素影响。首先，定位系统采用的姿态传感器有漂移累计误差。另外，地磁场是弱磁场，测量过程中很容易被传感器周围的环境所干扰[1]，使得姿态传感器测量的姿态不准确；其次，一些坐标变换的参数都人工测量得到的，必然地存在误差。为了降低定位方法的误差，本文作者提出基于BP神经网络的误差校正。

2.1 BP神经网络的原理

BP神经网络是一种利用误差反向传播算法的前馈型网络，是迄今为止应用最为广泛的神经网络。BP神经网络目前广泛用于函数逼近、模式识别、数据挖掘、系统辨识与自动控制等领域[2]。

图3所示的3层网络为例，具体说明BP网络学习算法[3]：

图3 三层BP神经网络

设训练样本的输入集合为P={P1,P2,P3，…，Pn}，输出集合为T={T1,T2,T3，…，Ty}。其中任意一个训练样本的输入为Pm={Pm,1,Pm,2,Pm,3，…，Pm,r} ，输出为tm={tm,1,tm,2,tm,3，…，tm,S2}，对应的网络输出为；输入层共有r个神经元，隐含层共有S1个神经元，输出层共有S2个神经元；隐含层第i个神经元对应的激活函数为，输出层第k个神经元对应的激活函数为。

当网络进行第t次训练，输入为第m个样本时：

（1）各层的输出

①隐含层第i个神经元的输出为：

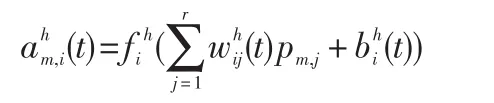
②输出层第k个神经元的输出为：

（2）定义误差函数为

（3）利用梯度下降法求各层权值的变化

①输出层第k个神经元和隐含层第i个神经元之间权值的变化量：

同理，输出层第k个神经元和隐含层第i个神经元之间阀值的变化量为：

②隐含层权值变化

隐含层第j个神经元与输入层第i个神经元之间权值的变化量为：

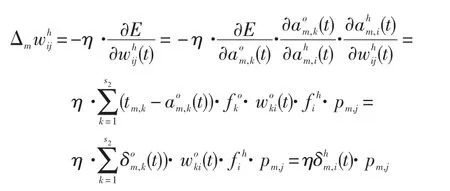
同理，隐含层第i个神经元和输入层第j个神经元之间阀值的变化量为：

因此，隐含层、输出层的权值和阀值的修正公式如下：

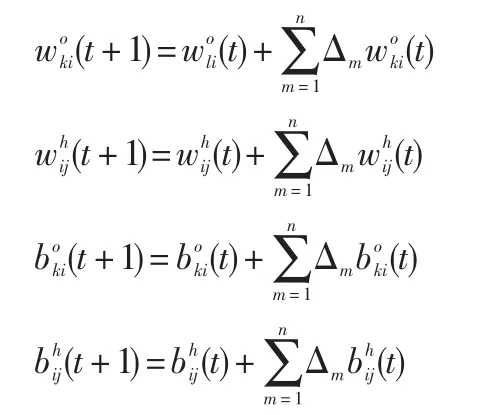
2.2 BP神经网络的设计

在进行BP网络设计时，一般应从网络的层数、每层中的神经元个数、初始值以及学习方法等方面来进行考虑[4]。

（1）网络的层数

理论上早已证明：具有偏差和至少一个S型隐含层加上一个线性输出层的网络，能够逼近任何有理函数[4]。所以，据此确定网络的层数为3层，仅有一个隐含层。

表1 S1=2，3，4，5，6，7，…，30时的网络训练结果

（2）每层的神经元数

由于输入、输出样本为点的三维坐标，因此输入层和输出层的神经元数均为3个。接下来选取多少个隐层节点才能满足系统精度的要求？这在理论上并没有一个明确的规定[5]。在具体操作时，通常的做法是对不同神经元数进行训练对比，确定一个最佳的节点数，然后加上一点余量即可。

采用traingd训练函数和learngd学习函数。为了节省训练时间，选择误差目标为net.trainParam.goal=0.14。通过改变网络隐含层的节点数，对比不同节点数下网络训练所需的循环次数和训练时间来确定一个合适的隐层节点数。各节点数的训练结果如表1所示。可以看出：当S1=11时较为合适，再加上2个神经元。所以，S1=13。

（3）初始权值的选取

初始权值的选取要合适。威得罗等[6]提出了一种选定初始权值的策略：选择权值的量级为 S1。对应地，在MATLAB工具箱中，可采用函数nwtan来初始化隐含层权值。但此策略只能用于第一隐含层，除此之外的隐含层的初始值在（-1，1）之间取随机数。

（4）学习速率的选取

学习速率决定每一次循环训练中所产生的权值变化量。与初始权值的确定过程一样，在确定一个神经网络的学习速率中，要对比几个不同的学习速率下，网络训练过程中误差平方和∑e2的变化情况。据此，通过对比，将学习速率确定为0.035。但是通常情况下，采取自适应学习速率这种方法来确定学习速率。

（5）期望误差的选取

在设计网络的训练过程中，期望误差也应当通过对比训练后确定一个合适的值[7]；

期望误差的选取与隐含层的节点数有关。前文将隐含层的节点数定为13，在MATLAB中，网络误差下降到0.001 73时，过好几分钟网络误差才会继续下降。因此，将期望误差选取为0.001 8，但是只针对traingd训练函数和learngd学习函数。

（6）BP算法的改进方法

能加快训练速度，避免陷入局部极小值的常用方法有：附加动量法、自适应学习速率法、误差函数改进法等。在此，采用附加动量和自适应学习速率这两种方法。

3 BP神经网络的MATLAB实现

在MATLAB中对所设计的BP神经网络进行实验验证，需要用到神经网络工具箱，该工具箱是在MATLAB环境下开发出来的[8]。

3.1 所设计的BP神经网络的MATLAB实现

clear all;

clc;

Fop=fopen(′P.txt′，′rb′);

[P，countp]=fscanf(Fop，′%f′，[3 inf]);Fot=fopen(′T.txt′，′rb′);

[T，countt]=fscanf(Fot，′%f′，[3 inf]);Fotc=fopen(′C.txt′，′rb′);[C，counttc]=fscanf(Fotc，′%f′，[3，inf]);

fclose(′all′);

P=P*1000;

T=T*1000;

C=C*1000;

[P，psp]=mapminmax(P);

[T，pst]=mapminmax(T);

C=mapminmax(′apply′，C，psp);

net=newff([-1 1;-1 1;-1 1;]，[13，3]，{′tansig′，′pure⁃lin′}，′traingd′，′learngd′，′mse′);

net.layers{1}.initFcn=′initnw′;

net.inputWeights{1，1}.initFcn= ′nwtan′;

net.biases{1，1}.initFcn= ′nwtan′;

net.layers{2}.initFcn=′initwb′;

net.inputWeights{2，1}.initFcn= ′rands′;

net.biases{2，1}.initFcn= ′rands′;

net=init(net);

net.trainParam.goal=0.000150;

net.trainParam.epochs=200000;

net.trainParam.show=25;

net.trainParam.showWindow=1;

net.trainParam.lr=0.035;

net.trainParam.mc=0.95;

Cyz=sim(net，C);

Cyz=mapminmax(′reverse′，Cyz，pst);

Cyz=Cyz/1000;

Fotc1=fopen(′C1.txt′， ′rb′); [C1， countt2] =fs⁃canf(Fotc1，′%f′，[3，inf]);

C1=C1*1000;

x=0;y=0;z=0;

for i=1:19

x=x+(Cyz(1，i)-C1(1，i))^2;

y=y+(Cyz(2，i)-C1(2，i))^2;

z=z+(Cyz(3，i)-C1(3，i))^2;

end

plot(wc);

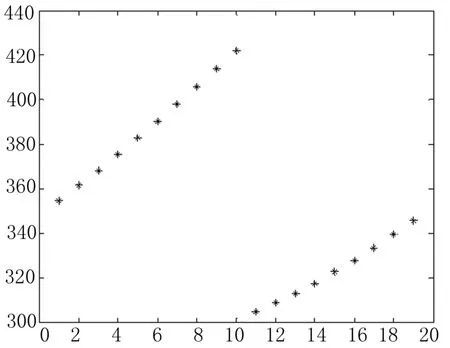
图4 校正前定位系统的误差

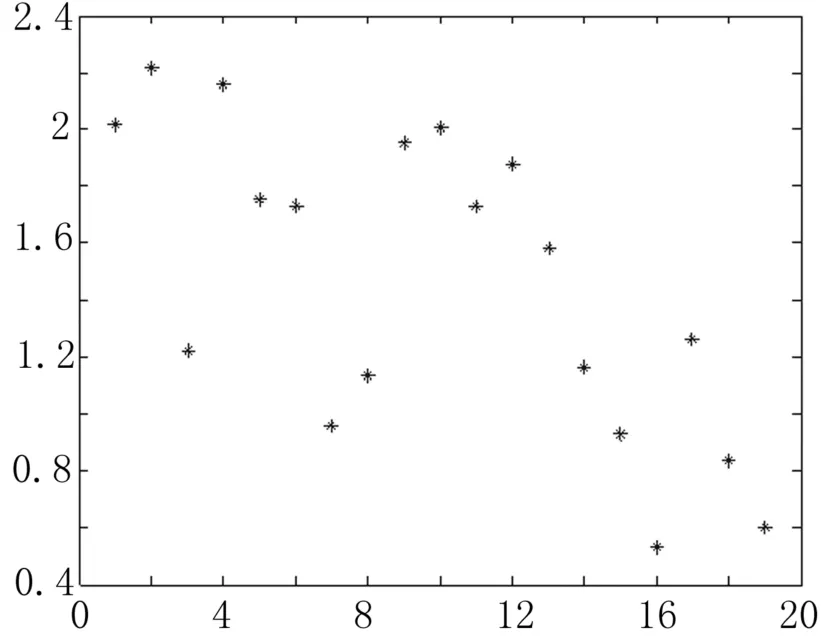
图5 校正后定位系统的误差

3.2 实验结果

待网络训练完成后，将19个验证点的坐标值输入训练后的网络，得到网络的输出值。然后，将输出值与实际值进行对比，得到误差。由图4、图5可以看出：基于19个验证点时，校正前系统的最小误差为304.810 7 mm，最大误差为422.320 6 mm；校正后系统的最小误差为0.531 7 mm，最大误差为2.2147 mm；因此所设计的BP神经网络能有效地降低所设计的定位系统的误差。