陶瓷抛光机空载阶段能耗建模与仿真

刘汉勇，李 骏，杨 柳

（广东工业大学机电工程学院，广东广州 510006）

0 引言

抛光砖是现代建筑行业中应用最为广泛的材料之一，由于其气孔率低、高硬度、高耐磨性、耐腐蚀、表面光亮如镜、色彩丰富多样的特点，倍受广大消费者青睐[1]。抛光工序作为抛光砖的生产工艺流程中必不可少的一道工序，消耗30%～40%抛光砖的生产能耗。抛光工序的节能降耗变得越来越迫切。而抛光工序中主要使用的机器就是陶瓷抛光机。为降低其能耗，首先应得到抛光机的能耗模型，再进行参数优化。

目前，机械加工设备能耗建模已经成为国内外研究的热点问题。2009年德国教授Verl[2]的研究团队在优化制造系统能量消耗方面也做了较为细致的研究工作，该研究团队利用仿真技术提出一种制造系统能耗建模的新方法。重庆大学刘飞教授[3]研究团队对机床主传动系统的能耗特征进行研究，建立数控机床主传动系统等主要耗能环节的能耗模型，进一步考虑机床多能量源的能耗特征，将能耗研究扩展到整个机床。广东工业大学杨海东教授【4-5】结合运动学方程和磨削深度理论，建立以瓷砖表面高度方差为评价指标的质量模型和瓷砖抛光的切削形成能耗模型，并仿真分析得出磨头转速、瓷砖进给速度等抛光工艺参数对抛光质量和能耗的影响，以多目标优化得到最佳的工艺参数组合，但并没有考虑到抛光机空载部分的能耗。

陶瓷抛光机具有加工机理复杂、多能耗类型、能量流动规律复杂等特性。针对这些问题，本文作者分析抛光机内部的能流模型，确定主要的耗能部分，建立其能耗模型。为验证能耗模型是否正确，对相应的模型进行误差分析。

1 陶瓷抛光机能流分析

以一种摆动式抛光机为研究对象。抛光机工作时，由滚筒带动传送带作水平移动，带动置于传送带上的瓷砖进给。同时，磨头在电机的驱动下进行旋转，气缸带动磨头使磨块缓慢地垂直压在瓷砖上进行抛光。由于磨块尺寸相对于瓷砖尺寸较小，为了加工整个瓷砖，横梁将在电机的驱动下进行摆动，带动瓷砖进行轴向移动[6]。

陶瓷抛光机工作过程中主要耗能为电能，在通过其内部结构转换为陶瓷砖抛光所需的机械能。陶瓷砖抛光过程需要的能耗可以分为抛光磨头旋转能耗、传动滚筒能耗、电气部分能耗以及辅助设备能耗（如液压系统能耗、冷却水耗能）。陶瓷抛光机各个部分能耗形式及其作用如图1所示。

由图1可知，陶瓷抛光机的能源消耗可以看成由3个部分组成。机械部分都是由电能转化为各种形式的机械能，机械传动部分又可以分成2个子模块。磨头旋转部分，主轴电机带动磨头旋转，提供磨头切削瓷砖所需的切削力。瓷砖进给部分，进给电机带动滚筒旋转，滚筒带动传送带运动使瓷砖以匀速运动水平进给。电气控制部分，主要是电气控制柜耗能，提供PLC控制器等所需的电能。辅助系统部分，气压系统、冷却泵等则提供磨头垂直进给、冷却和润滑等必要的辅助功能，这是由电能转化为液压能和气压能。

对于抛光机来说，电气控制模块、辅助系统模块是相对简单，耗能较少且相对固定。这部分能耗是在机器出厂时就几乎确定，可调节范围很小。而机械部分消耗大量的电能，而且涉及众多工艺参数，可调节范围较大。当抛光机进行抛光时，其机械部分能耗可以看成是切削形成能耗与抛光机空载能耗的叠加。本文作者将空载能耗定义成抛光磨头、传动滚筒两个机械部件的能耗相加。这部分能耗既存在于当抛光机空载时，也存在于抛光机对瓷砖进行抛光时，其消耗的能耗占抛光机机械部分的绝大部分。

2 抛光机空载能耗建模

2.1 抛光磨头能耗

电机通过带轮、齿轮带动磨头电机旋转，从而使得磨头对瓷砖进行抛光。为方便计算，将抛光磨头工作原理图进行相关简化，简化后的结果如图2所示。

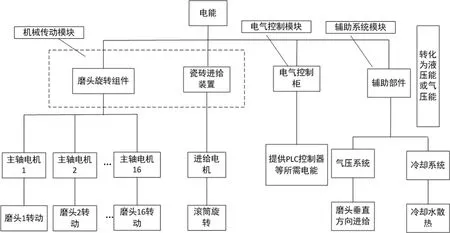
图1 陶瓷抛光机的能耗模块及其作用

图2 磨头简化原理图

对磨头进行受力分析。由图3可知，磨头一共受4个力的作用，分别是对瓷砖进行抛光时瓷砖给磨头（磨块）的摩擦力Ff，液压系统对抛光磨头的力F1使其向下的运动，瓷砖表面对抛光磨头的支撑力F1′以及主轴给抛光磨头传递的转矩T。

图3 磨头受力分析图

设磨头直径为D，磨头重量为m，得磨头转动惯量[7]：

磨头转速为n，则其对应的角速度ωL为：

磨头对瓷砖进行抛光时，磨头转速一直保持不变，故磨头的负载功率PL为：

磨头的线速度v为:

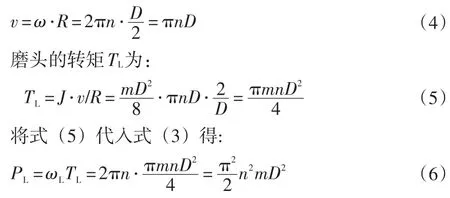
假设每对齿轮的转速比分别为j1、j2，则对应的机械系统传动比j为：

磨头转速为n，折算到电机轴上的转速nM为：

对应的磨头电动机的角速度ωM为：

假设每对齿轮的效率分别为η1、η2，则对应的电动机拖动生产机械运动时的传动效率ηc为:

因此，折算到电机的转矩TM为:

式中：ω代表磨头角速度，rad/s；m代表磨头质量，kg；D表示磨头直径，mm；η1表示第一对传动齿轮的传动效率；η2表示第二对传动齿轮的传动效率。

图4 传动滚筒受力分析图

2.2 传动滚筒能耗

传动滚筒是陶瓷抛光机的重要部件，传动滚筒受力主要是摩擦力和磨头工作时产生的切削力。对传动滚筒进行受力分析，如图4所示。工作时，传送带与滚筒之间产生的摩擦力为 f1，瓷砖放置在传送带上，瓷砖与传送带之间的摩擦力为 f2，瓷砖与磨块之间产生的摩擦阻力为Ff。由切削变形引起的法向力为Fnc，由于摩擦引起的法向力为Fns，由于切削变形引起的切向力为Ftc，由于摩擦引起的切向力为Fts。瓷砖进给速度为v0。

对于单颗磨粒而言，由摩擦引起的法向磨削力为[8]：

在纯剪切变形条件下，由切削变形而引起的单颗磨粒法向磨削力为[8]：

式中：K表示单位磨削面积的磨削力；A表示磨削截面积。

故单颗磨粒的法向磨削力Fgn为：

假设一个磨块上有n个磨粒，磨粒受力都相等，则对应的磨块上的法向磨削力Fn为：

瓷砖表面与磨块之间产生的摩擦阻力Ff为：

式中：μ1为磨块与瓷砖之间的摩擦因数。

传送带与滚筒之间的摩擦力 f1为：

式中：m为磨头的重量，m2为抛光砖的重量，m3为传送带的重量，μ2为传送带与滚筒之间的摩擦因数。

瓷砖与传送带之间的摩擦力 f2为:

式中： μ3为抛光砖与传送带之间的摩擦因数。

传动滚筒上的圆周驱动力FA为：

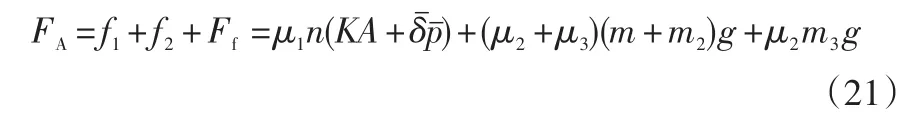
假设瓷砖进给速度为v0，则传动滚筒功率PA为

3 误差分析

为验证建立的空载阶段能耗模型的可行性和准确性，需要把计算结果和通过智能电表测量的数据进行比较。当误差范围在±3%～±8%时可认为建立的模型是可行的、准确的。磨粒在磨具表面上的分布并不均匀，且高低参差不齐；另外由于磨削运动的关系，使压入一定深度的磨刃不会参加抛磨工作。因此，实际参加磨削工作的磨刃数会少于磨具表面的磨刃数。在加工过程中，抛光机输入设备的工艺参数实际上难以保持恒定。为了保证仿真实验的正确性，做出以下假设：

（1）加工的磨粒不会磨损或脱落;

（2）参加磨削的个点压强恒定不变;

（3）抛光过程中其他的工艺参数保持不变。

3.1 抛光磨头能耗误差分析

抛光磨头仿真过程中实验参数设定如表1所示，抛光磨头耗能随磨头转速的变化理论值和计算值如图5所示。

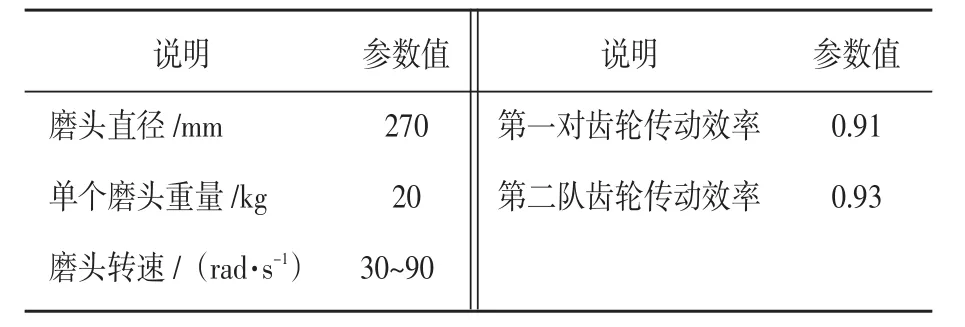
表1 抛光磨头仿真参数表

图5 抛光磨头能耗误差分析

3.2 传动滚筒能耗误差分析

传动滚筒仿真过程中实验参数设定如表2所示，抛光磨头耗能随瓷砖进给速度变化的理论值和计算值如图6所示。

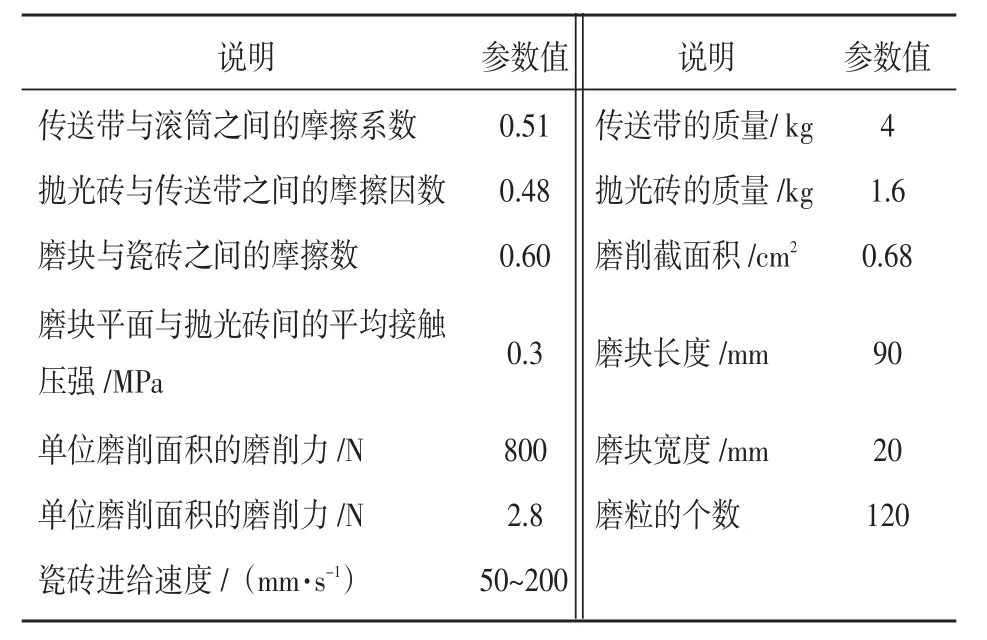
表2 传动滚筒仿真参数表

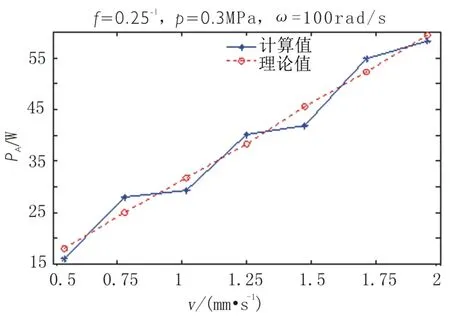
图6 传动滚筒能耗误差分析

由图6可知，在其他参数都确定的情况下，传动滚筒进给速度越大，传动滚筒的耗能也就越多。传动滚筒能耗的计算值和理论值是在误差范围内的。这表明建立的传动滚筒能耗模型是合理的。

3.3 仿真结果分析

从图5、6可知，当磨头角速度、瓷砖进给速度、横梁摆动频率增大时，其对应的机械部分能耗也将增大。能耗的理论值和计算值也都在误差范围内，表明建立的能耗模型是可行的、合理的。

4 结论

分析抛光机内部的能流规律，并根据其电能的转化形式将抛光机能耗分成机械部分耗能、辅助部分耗能和电气控制柜耗能3个部分。结合磨头角速度、瓷砖进给速度、横梁摆动频率对抛光机空载阶段的影响，建立对应的能耗模型，得到抛光机空载阶段的能耗分布规律。为验证建立的能耗模型是否合理，使用多组参数在计算机上用Matlab软件进行仿真实验。仿真结果表明建立的抛光机空载阶段能耗模型是合理的。这为进一步对抛光机进行能耗优化得到最优的工艺参数有十分重要的意义。