基于支持向量机递归特征消除和特征聚类的致癌基因选择方法
2018-10-09叶小泉吴云峰
叶小泉,吴云峰
(厦门大学信息科学与技术学院,福建省智慧城市感知与计算重点实验室,福建厦门361005)
癌症通常缘于正常组织在物理或化学致癌物的作用下基因组发生突变,即基因表达水平的改变,使得许多生物过程失调[1].而基因表达信息可以通过基因芯片技术测得,基因芯片(通常也称为DNA微阵列或生物芯片)是附着于固体表面的微观DNA斑点的集合.在分子生物学领域,根据核苷酸分子在形成双链时遵循碱基互补原则,研究人员能够使用基因芯片测量大量基因的表达水平信息,从而得到基因表达谱.因此,若利用这些基因表达谱数据确定出与癌症有密切关系的基因,将对癌症的诊断和治疗发挥重要意义[2].
由于存在与测定相关的成本问题,基因表达谱数据具有高维小样本的特性.较高的维数是获得问题准确描述的有力保障,但它又难以避免地会引入大量冗余和与类别无关的噪声信息,这给传统的机器学习方法带来了挑战.因此,从成千上万个基因中判断出在不同疾病类别上具有差异性表达的少量致癌基因前,需要剔除掉大量无关基因,而特征选择是一种有效的手段.
在利用基因表达谱数据进行致癌基因选择的问题上,Golub等[3]对急性白血病亚型识别和致病基因的判别进行了研究,用信噪比(SNR)指标来作为基因对样本类别的区分能力,其研究结果表明白血病亚型之间在基因表达上的差异可以通过一系列基因的表达水平检测来进行临床诊断,并可以由此指导后续治疗方案的制定.该方法运行速度较快,适用于高维数据,但由于其不能识别冗余基因,结果常常不尽人意.另外,Guyon等[4]将支持向量机(SVM)与递归特征消除(RFE)相结合提出了SVM-RFE算法,该方法通过SVM每个维度权重的绝对值来度量对应特征的重要性,每次迭代删除权重排名靠后的一个特征,取得了良好的效果.但是它每次迭代只删除一个特征,在高维数据中仍耗时较长.因此Ding等[5]对它进行了改进,使得每次可以按比例删除特征,提高了计算速度,但同时也发现所选的特征对每次迭代删除的特征表现得十分敏感.此外Yousef等[6]提出了一种基于SVM的递归聚类特征消除(SVM-RCE)算法,该方法使用聚类方法对特征集进行聚类,随后利用SVM对各个特征类进行评分,最后迭代删除得分最低的那些特征类.此类递归聚类特征选择算法能够有效去除大量无关特征,但最后剩下的部分特征之间存在相似性较高、容易导致特征冗余的问题.因此,在特征排序和SVM-RFE算法的基础上,本研究将二者结合并引入聚类算法,提出一种新的、适用于基因表达谱数据的特征选择方法:K类别SVM-RFE(K-SVM-RFE).
1 相关工作介绍
在具有高维小样本特性的基因表达谱数据中,一个快速且有效获得致癌基因的方法是对特征排序.因此,在K-SVM-RFE算法中,利用基于SNR的特征排序方法剔除大量无关基因,将剩余基因利用K均值算法聚成多个类别,并利用SVM-RFE算法精选致癌基因.
1.1 基于SNR的特征排序
SNR通常用来表示电子信号中信号与噪声的比例,而在特征选择中,可以用SNR指标来度量特征的重要性,进而对特征排序.Golub等[3]的研究表明基于SNR的特征排序方法是一个快速且有效的致癌基因判别方法.基因gi的SNR数值RSN通过下式计算得到:
(1)
其中:u+(gi)和u-(gi)分别表示第i个基因gi在阴性类别和阳性类别的平均表达值;σ+(gi)和σ-(gi)分别表示基因gi在两个类别中表达水平的标准差.
用式(1)来衡量每个基因的重要性,值越大说明该基因越重要.若某一基因在不同类别中的分布均值相等,那么它的RSN等于零,则该基因便被认为是无关基因而剔除.
1.2 K均值聚类算法
K均值聚类算法[7]是最经典的聚类方法之一,它基于观测对象间的相似度将对象划分不同类别,使得类内具有较高的相似度,而类间的相似度较低.对于给定的一组样本数据(x1,x2,…,xn),现要将其划分为K个子集合(类别),S={S1,S2,…,SK},K均值的划分思想是:先从n个样本中随机选出K个样本作为初始聚类中心,随后将剩余样本分别划入与其距离最近的聚类中心的相应类别中,使得类内总距离达到最小,其目标函数可以表示为:
(2)
其中ui表示集合Si的聚类中心点.所有样本的类别划分完毕后需要更新各个类别的中心点,第t+1次的聚类中心通过下式计算:
(3)
随后对各个样本重新划分类别,重复以上过程直到中心值的变化可以忽略不计或者达到最大的迭代次数.
1.3 SVM-RFE特征选择算法
SVM是一种基于统计理论的分类方法,它利用核函数将普通低维空间中难以用一条直线分开的数据映射到一个较高维度的空间中,使其达到线性可分的目的.在SVM超平面上的每个维度对应着输入数据集中的每个特征,因此可以把超平面上各个维度权重的绝对值看作该维度(或特征)的贡献(或重要性).所以,权重的绝对值便可以用来对特征排序,从中选出关键特征.SVM-RFE便是基于此思想的嵌入式特征选择方法,最初由Guyon等[4]提出,它是将SVM与RFE的后项搜索方法相结合的产物.SVM-RFE的特征选择过程如下所示.
输入:训练数据集E(n个样本,m个特征),类标签(n,1).
1) 初始化当前特征集合Enow为原始数据集,最优特征集合Ebest为空,最优特征子集分类正确率Sbest为0.
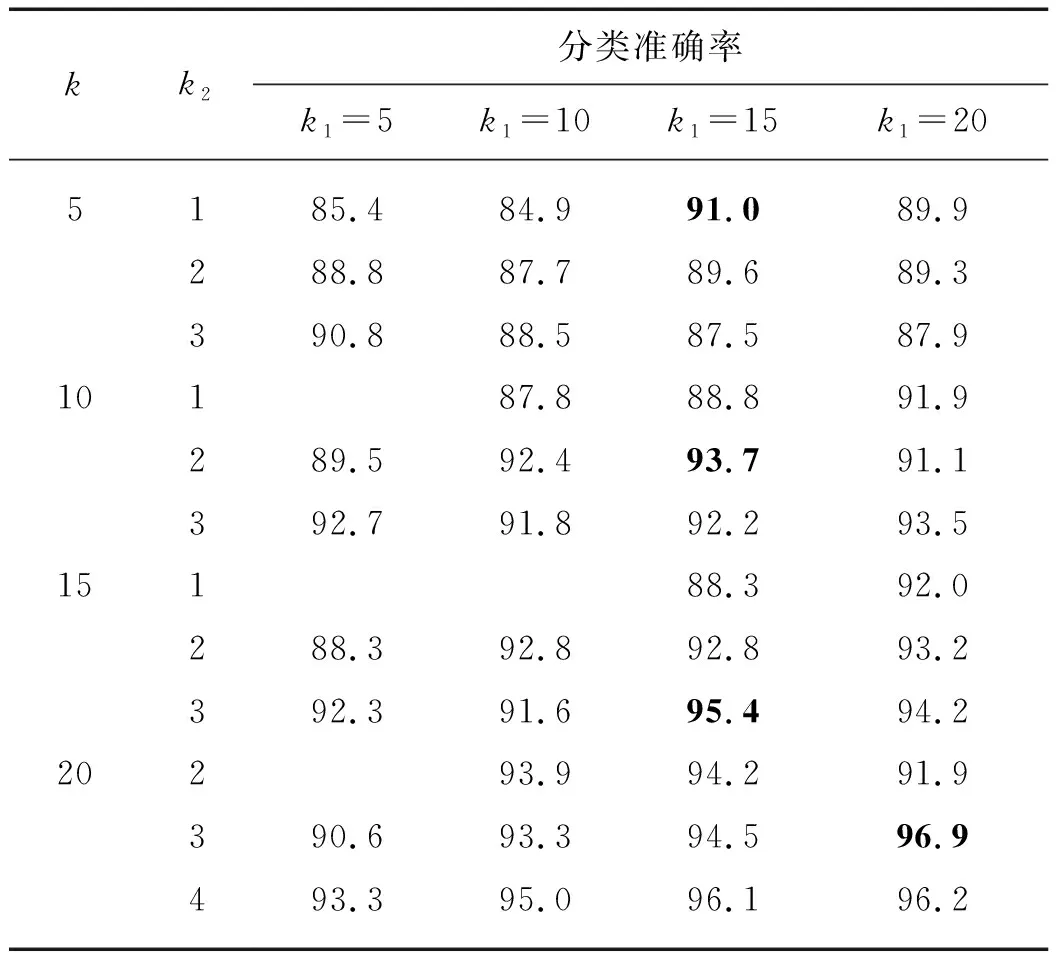
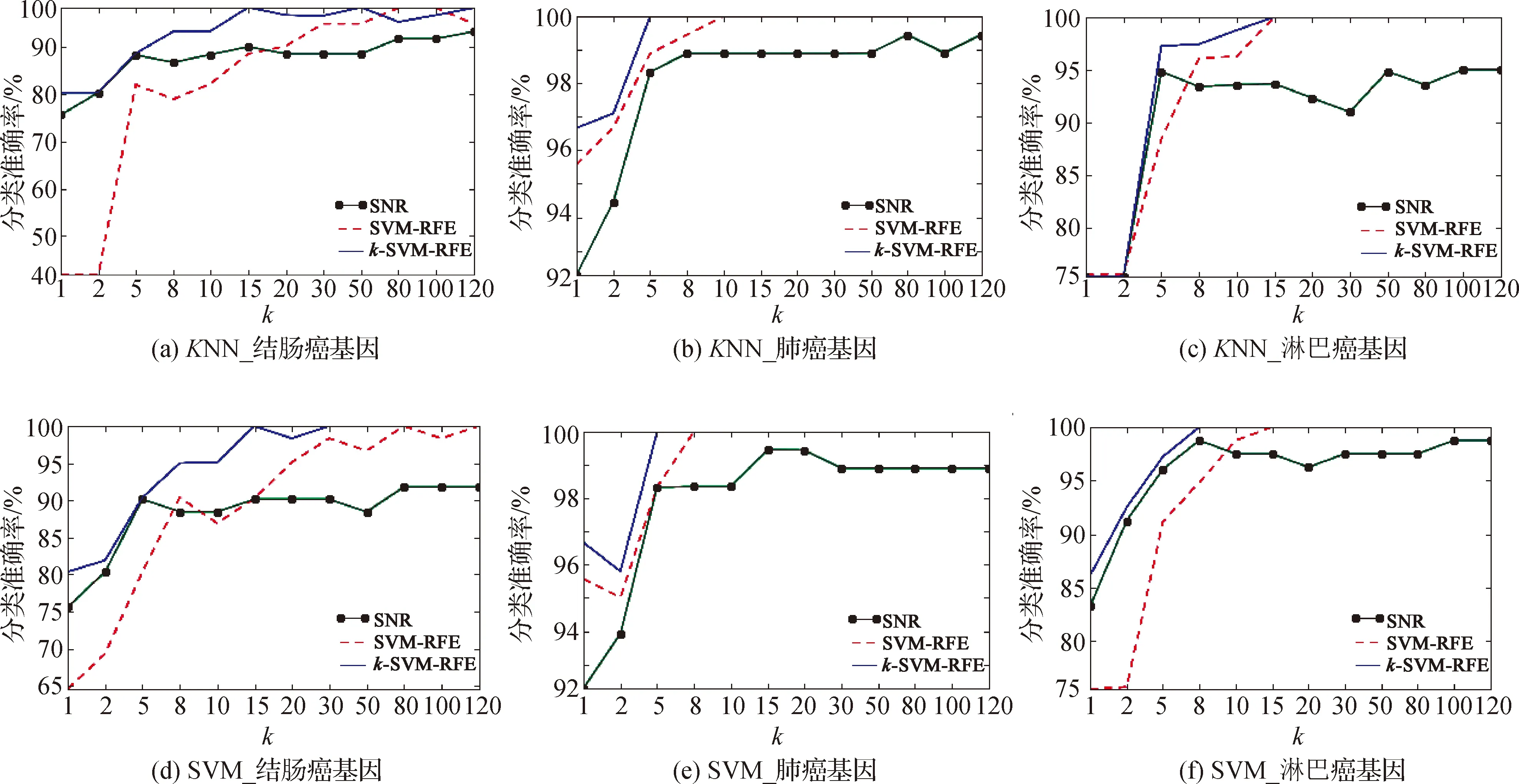
2) 设置每次删除的特征数量比例p(0 3) 重复以下步骤,直至当前特征集合Enow为空: 由Enow建立SVM模型,得到正确率评估值Snow; 按特征权重的绝对值|w|降序排列Enow中的特征; 删除当前子集Enow中排名靠后的p%个特征; 若当前特征子集Enow的正确率Snow大于Sbest:Ebest=Enow. 输出:最优特征子集Ebest. SVM-RFE算法用SVM超平面的每个维度的权重绝对值来代表相应特征的重要性,随后通过权重对特征按从大到小排列.从降序排列的特征集合开始,每次删除排名最后的那个特征;随后继续使用SVM在剩余特征集合上训练分类器,再删除特征;如此多次重复进行直到该特征集合为空,或者达到了用户设定的特征数量为止.由于其优异的性能表现,SVM-RFE算法广泛用于图像处理,文本分析,生物信息处理等领域. 特征排序算法(如基于SNR的特征排序算法)能够快速且有效地得到在不同类别中具有差异性表达的特征,特别是对于具有高维小样本特性的数据,特征排序算法可以迅速去除无关特征.但是,在排名靠前的特征中,往往部分特征之间具有较高的相似性,造成了特征的冗余,这将会对少数关键特征的确定造成困扰,进而影响最终的分类性能. 因此,特征排序方法能够高效地去除无关特征,但是不能识别和去除冗余特征,它适用于关键基因的初步筛选.基于此,本研究提出一种三阶段的基因选择方法K-SVM-RFE.首先,利用SNR指标计算各个基因的权重,并按权重降序排列基因,初步过滤掉大量权重值较低的基因;其次,为了去除冗余基因,将初步筛选后基因通过聚类算法聚成k1个类别,并对各个类别利用SVM-RFE方法选出k2个具有代表性的基因,组成新的基因集合F;最后,再次利用SVM-RFE算法从F中选择出k个关键基因.算法描述如下所示,流程如图1所示. 输入:原始数据集(n个样本,m个特征),类标签(n,1),选择基因数量k. 1) 将原始数据预处理,处理结果记为D. 2) 特征排序算法从D中筛选出d个基因,记为f1,其维度为(n,d). 4)i从1循环至k1,令f2=f2+SVM-RFE(ci,k2),其中SVM-RFE(ci,k2)表示使用SVM-RFE算法从ci中选择出k2个关键基因. 5) 使用SVM-RFE算法从f2中选择出k个关键基因. 输出:k个关键基因. 值得注意的是,K-SVM-RFE方法中共涉及到3个关键参数,分别为k,k1和k2.其中,k为最后SVM-RFE算法选择的基因个数,也即最终输出的基因数量;k1为聚类算法所聚的类数;k2为各个类别中使用SVM-RFE方法选择的基因数.k,k1和k2均可通过用户设定,但为了保证最后一次的SVM-RFE方法能够选出足够的k个基因,应至少满足如下关系: k1×k2≥k. (4) 在本文中3.2节我们将进一步讨论这3个参数的设置关系,以使K-SVM-RFE算法所选择的特征达到最佳的分类效果. 实验主要以分类准确率来比较本研究所提出的K-SVM-RFE算法与基于SNR的特征排序算法以及SVM-RFE算法在分类上的性能差异.为了验证K-SVM-RFE算法的有效性,本研究以3个公共的基因表达谱数据集作为实验对象,包括结肠癌基因表达谱数据集[8]、淋巴癌基因表达谱数据集[9]以及肺癌基因表达谱数据集[10].这些数据集均可以从生物识别研究计划的网站[11]下载得到,其数据构成如表1所示: 表1 实验数据集 在数据预处理阶段,由于原始数据集中存在着基因表达水平全为0的数据列,同时也存在着少量的基因有表达值,但基因信息为空白的数据列,因此在获得数据之后,本文中将这些全0列和信息不全的基因列作为问题数据剔除.随后将数据离散化为0,1,2的整数,为下一步基因的分析研究做好准备工作.对数据进行离散化处理,一方面是由于基因表达谱数据的数值表征基因的表达水平,相邻数据之间不具有连续性,另一方面数据离散化也可以看作是去噪的一个过程. K-SVM-RFE算法中共涉及到4个参数,分别为待选择特征的数量k,初步筛选特征数量d,K均值聚类算法所聚的类数k1和在各个类别中使用SVM-RFE算法选择的基因数k2.其中初步筛选特征的作用是首先去除大量无关的噪声特征,降低下一过程的计算复杂度,因此d的选择对实验结果影响不大,它满足远小于初始特征数量且稍大于待选特征数量即可.因此本研究在d取600时进一步探究k与k1和k2之间的设置关系.本实验以结肠癌基因表达谱数据集为实验对象,以K最近邻(KNN)作为分类器,设置不同的参数,采用五折交叉验证的方式重复实验10次,取分类准确率的平均值作为最终的结果,实验结果如表2所示.由第2节知,k1与k2需要满足式(4),所以表中不满足此条件的实验设为空. 表2 不同参数下所选特征的分类准确率 在表2中,加粗的数据为所选特征数量k条件下的最佳分类准确率结果.可以看出,当k取15和20时,分类准确率均在k1与k相等,k2取3时达到最大值,此时有k1×k2=3k;当k取5和10时,虽然最大准确率不在k1=k条件下,但是依然满足k1×k2=3k的关系,且如果取k1=k,k2=3,其结果也依然较好. 因此,设置聚类算法所聚的类数与要选择的特征数量相等,即k1=k且k2=3时,K-SVM-RFE算法所选特征能够得到较好的分类性能. 为了分析比较不同特征数量对特征评价的准确性,实验分别测试重要特征数量为1,2,5,8,10,15,20,30,50,80,100,120时的分类性能.实验中涉及到的一些参数包括:基于SNR的特征排序方法初步筛选出d=600个重要基因,k,k1与k2的取值根据3.2节取k1=k,k2=3;SVM-RFE算法每次迭代删除的特征比例设为0.1,其他参数保持默认.另外,在分类结果验证上,特征选择算法选出的关键基因分别作用于KNN和以径向基为核函数的SVM这2个分类器.其中KNN分类器原理简单,易于理解与实现,而SVM分类器在解决小样本、非线性及高维模式识别中表现出许多特有的优势,将K-SVM-RFE算法同时作用于这2个分类器,可以验证K-SVM-RFE算法所选特征在不同分类器上的适用情况.实验采用五折交叉验证的方式,取5次结果的平均值作为最终实验的准确率,实验结果如图2所示. 从图2中可以看出,K-SVM-RFE算法在2种不同的分类器(KNN和SVM)下、3个不同的数据集和多个不同的关键基因数量上均展现出了比SVM-RFE算法和基于SNR的特征排序方法更好的分类准确率.首先,随着提取关键特征数量的递减,K-SVM-RFE算法与经典的SVM-RFE算法的分类准确率在逐步拉开差距,K-SVM-RFE算法在分类表现上较SVM-RFE算法有较大提升,表明K-SVM-RFE算法在提取少量关键基因上的有效性.其次,在所有的结果中,基于SNR的特征排序方法所选择特征的分类准确率均不能达到100%,表明了该过滤式特征选择方法不能去除冗余特征的局限性,而K-SVM-RFE算法能够进一步去除冗余特征,达到了特征精选的效果. 另外,对比相同数据集不同分类器条件下的结果,可以发现,以SVM作为分类器的分类结果总体都好于KNN分类器的结果.特别是淋巴癌基因表达谱数据集上,SVM的分类准确率在特征数量为8时达到100%,而KNN分类器则在特征数量为15时分类准确率才达到100%.产生这样的差异一方面是因为K-SVM-RFE算法基于SVM学习,所以用SVM进行分类可取得较好的结果;另一方面也是因为SVM在做分类器时它的惩罚因子的值主要是由样本的数量而不是特征数量决定的,因此在各种数据集上应用此模型都会有比较稳定的分类性能. 图2 不同分类器(KNN、SVM)在不同基因(结肠癌、肺癌、淋巴癌基因)表达谱数据集下3种特征排序方法的分类正确率与k的变化关系图Fig.2 Classification accurate rates of different classifiers (KNN,SVM) with respect to kon different genes (colon, lung, andlymphoma gene) expression datasets solved by three feature sorting methods 本研究将聚类算法与SVM-RFE方法相结合,提出了一种新的面向基因表达谱数据的特征选择方法K-SVM-RFE,以多个基因表达谱数据为实验对象,并通过2个分类器分别验证所选基因的分类效果.研究结果表明了K-SVM-RFE算法在致癌基因识别上的有效性,特别是在精选少量致癌基因上,性能更佳. 在取得上述成果的同时,本研究还有许多有待进一步研究的地方.如本文中实验数据均只有2个类别,对于多类别数据的分类性能还有待进一步研究;SVM-RFE和其他聚类算法的结合效果以及k1和k22个参数的最佳设置,也有待进一步探讨.2 K-SVM-RFE基因选择方法
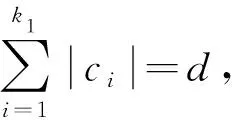
3 实验和结果分析
3.1 实验数据

3.2 参数分析
3.3 分类准确率的分析
4 结 论
