NSD序列的Chover型重对数律
2018-10-09陆冬梅
黄 辉, 陆冬梅, 胡 涛
(1. 长春理工大学 光电信息学院, 长春 130022; 2. 首都师范大学 数学科学学院, 北京 100048)
1 引言与主要结果
定义1[1]如果对任意的x=(x1,…,xn)∈n,y=(y1,…,yn)∈n, 有
φ(x∨y)+φ(x∧y)≥φ(x)+φ(y),
定义2[1]对于随机向量X=(X1,X2,…,Xn), 如果满足
(1)
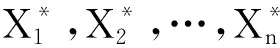
研究表明, 由NSD推不出NA(negativelyassociated)[1], 但由NA可以推出NSD[2], 即NSD序列是包含独立和NA序列在内的一类更广泛的相依序列. 目前, 关于NSD序列的研究已有很多成果[3-9].
定义3[10]对于随机变量X, 如果
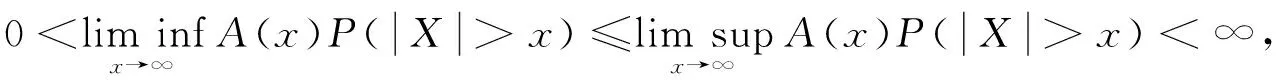
(2)
则称X为α>0重尾的. 其中A(x)是指数为α的正则变化函数, 即
∀t>0.
令B(x)=inf{y:A(y)≥x}为A(x)的广义逆函数, 则B(x)是指数为1/α的正则变化函数. 易推得式(2)等价于
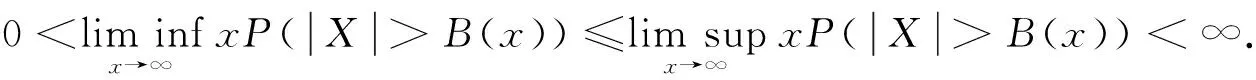
(3)
显然X为α重尾的比X是特征指数为α的随机变量条件更广泛. 下面假设X为α重尾的,B(x)定义如上.
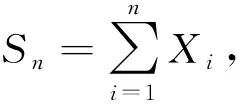
目前, 关于Chover重对数律的研究已有很多结果[10-18], 但NSD序列的Chover重对数律研究尚未见文献报道, 本文讨论NSD序列的Chover重对数律, 主要结果如下.
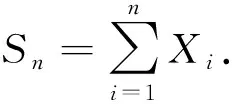

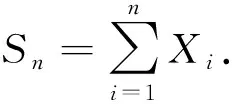
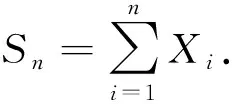

注1定理2~定理4不仅将文献[15]中结论推广到NSD序列的情形, 且定理2~定理4所得的结论更具普适性.
注2定理3即为NSD序列情形下的Chover重对数律, 将文献[10]中定理1的部分结果推到NSD序列的情形.
2 主要结果的证明
引理1[10]假设X为α>0重尾的,B(x)如上定义, 则对于任意的x>0, 当p>α时,

当0 其中c1>0,c2>0均不依赖于x. 引理2[1]如果(X1,X2,…,Xn)是NSD的,g1,g2,…,gn均为非降函数, 则(g1(X1),g2(X2),…,gn(Xn))也是NSD的. 引理4[4]设{Xi,i≥1}是NSD序列, 则存在正常数C, 使得对任意的≥0,n≥1, 有 采取循环证法1)⟹2), 2)⟹3), 3)⟹1). 记an=B(nf(n)). Ⅰ) 证明1)⟹2). 首先考虑0<α< 1, 由Chebyshev不等式、 式(3)及引理1可得 其次考虑α≥1. ∀i≥1, 令 由EXi=0并结合引理1, 可得 从而当n充分大时, 对∀ε>0, 有 中国传统道家思想强调无为而治,为数学课堂留白艺术提供了哲学基础,留白时看似无为却有所为.美学中常追求以虚衬实、虚实相生的境界,则为数学课堂留白艺术提供了美学基础.除此之外,“等待时间”理论和参与者知识观也为数学课堂留白艺术提供了丰富的理论基础. 当α≥2时, 结合Jensen不等式, 类似上述推导可知 其中q>α≥2. 结合式(4)~(6)可知 1)⟹2)证毕. Ⅱ) 2)⟹3). 因为任取正整数n, 总存在非负整数k, 使得2k≤n<2k+1, 且存在t∈[0,1), 使得n=2k+t, 则由2)可得 进一步有 注意到B(x)是指数为1/α的正则变化函数, 因此 2)⟹3)证毕. Ⅲ) 3)⟹1). 由3)及an=B(nf(n))、Xn=Sn-Sn-1、f(x)>0在x→∞时是拟增的, 得 Ⅳ) 证明4)⟹5). 任取正整数M, 由式(3)知 (7) 这与式(7)矛盾. 因此 从而 注意到B(x)是指数为1/α的正则变化函数, 于是可知 即5)成立. 这与4)矛盾. 因此 综上, 定理2证毕. 利用定理2和式(3), 类似文献[12]中定理2的证明可得结论.
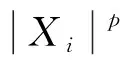
2.1 定理2的证明
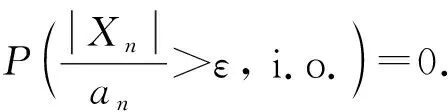
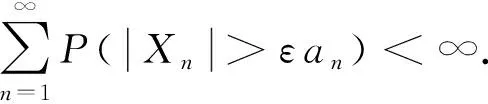
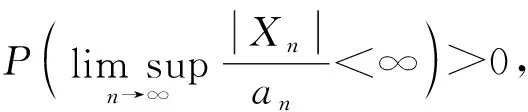
2.2 定理3的证明
2.3 定理4的证明