化学反应扩散模型的奇异摄动问题

宋 莹, 孙 宁

(吉林大学 数学学院, 长春 130012)

1 引言与预备知识

随机动力系统的退出问题, 即考虑位于确定型动力系统稳定态吸引域中的轨线在随机噪声驱动下离开吸引域退出点的概率分布和退出时间, 该问题在原子与分子物理、 化学动力学、 滤波理论以及群体遗传学等领域应用广泛[1-8]. 文献[1,9]研究表明, 如果粒子所处的介质是热平衡状态的, 则化学键粒子的变化可用如下Langevin方程描述:

引理1[1,9]当β充分大时, 系统(1)-(2)等价于Kramers-Smoluchowski方程:

dx=-

(3)

其中s=βs′.

(4)

τε=inf{t≥0|xε(τ)∈∂Ω,xε(0)=x∈Ω}.

引理2[2]方程(4)首次退出时间τε的期望Exτε=vε(x)满足如下边值问题:

文献[3]利用奇异摄动方法构造了方程(4)首次退出时间的渐近展开式; 文献[10]给出了上述结果有效性的理论证明; 文献[11]对具有光滑势垒和尖翘势垒的退出点问题给出了化学反应速率公式, 简化了文献[1]结果的条件, 并将其推广到高维情形; 文献[12]进一步对非特征边界以及特征边界两种情形运用匹配渐近展开法得到了首次退出时间的渐近表达式. 上述关于方程(4)退出问题的渐近分析研究只得到了退出时间的零阶近似, 本文利用奇异摄动方法给出方程(4)退出问题的一阶近似.

引理3[13]设x∈n(n≥2), f(x),g(x)是光滑标量函数, 且f(x)在x0处取得最大值, 则

其中Hf(x0)表示f在x0处的Hessian矩阵的行列式.

2 主要结果

对方程(4)做如下假设：

(H1)b(x)是Ω上的光滑向量场, 且φ在∂Ω上的最小值点都是孤立的;

(H2) 系统

dx(t)=b(x)dt

(7)

在Ω中有唯一渐近稳定的平衡点x0, Ω是x0的吸引域, 且

做变换

vε(x)=C(ε)eK/εu(x),

当ε→0时, 方程(8)退化为

b·u=0,x∈Ω.

(10)

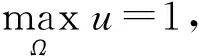
为求方程(5)的内部解, 做n维球坐标变换:

其中: 0≤r<+∞; 0≤θ1,θ2,…,θn-2≤π, 0≤θn-1≤2π. 则

其中

记(θ1,…,θn-1,r)=(θ,r), 再做变换y=-dist(x,∂Ω)=r-R,x∈Ω, 则边值问题(8)-(9)变为

其中:γ为∂Ω的外法向量;σ为∂Ω的切向量. 显然, (x1,…,xn)∈∂Ω对应于y=0. 设

定理1设系统(4)满足(H1),(H2), 且当(x1,…,xn)∈∂Ω时,b·γ<0. 则系统(4)从x0∈Ω出发的解x(t)首次退出时间期望Exτε的渐近表达式为

其中:

证明： 由上述分析知, 边值问题(11)-(13)在∂Ω附近存在边界层, 且边界层厚度为O(ε). 令y=εz, 则边值问题(11)-(13)变为

设边值问题(16)-(18)的解有如下形式:

u=u0+εu1+ε2u2+….

(19)

将式(19)代入式(16), 并对比ε的同次幂系数得

由边值条件(17),(18)得

方程(20)满足边值条件(22)的解为

u0(θ,z)=1-e-b10(θ)z.

将u0(θ,z)代入方程(21), 并利用边值条件(23)解得

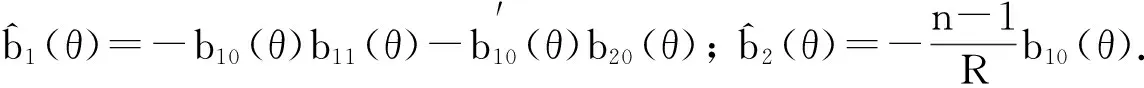
从而

下面确定常数C(ε)和K. 将方程(5)两端同乘e-φ/ε并写成散度的形式, 得

εe-φ/εvε=-e-φ/ε.

(24)

对式(24)在区域Ω上积分, 并由散度公式, 得

(25)

由引理3, 当ε→0时, 有

(26)

又

故

(27)

证毕.

假设:

(H3) Exτε在∂Ω的切方向是慢变的.

定理2设系统(4)满足(H1)～(H3), 且当(x1,…,xn)∈∂Ω时,b·γ=0. 则系统(4)从x0∈Ω出发的解x(t)首次退出时间期望Exτε的渐近表达式为

其中:

设边值问题(28)-(30)的解有如下形式:

u=u0+μu1+….

(31)

将式(31)代入方程(28), 并对比μ的同次幂系数得

由边值条件(29),(30)知,

方程(32)满足边值条件(34)的解为

将解u0(θ,z)代入方程(33), 并利用边值条件(35)得

于是

从而

下面确定常数C(ε)和K. 由式(25),(26)及

可得

证毕.