新工科背景下微积分课程体系重构与教学内容改革的研究与实践——以我校微积分课程教学为例

罗 琳

(上海第二工业大学 文理学部,上海201209)

0 引言

众所周知,微积分课程是高等学校工科类专业学生必修的一门重要通识基础课程。通过这门课程的学习,学生能够系统地掌握微积分的基本知识,必要的数学理论基础和常用的微积分计算方法。其主要目的一方面是为了培养学生的逻辑思维能力和微分积分运算能力,使学生能应用微积分知识建立实际问题的数学模型,解答模型,最终解决实际问题的目的;另一方面也使学生能够利用微积分课程知识为其他后续课程如工程数学课程(复变函数、积分变换、概率论与数理统计等)和专业基础课程(普通物理、电工基础、工程力学等)的学习奠定必要的现代数学基础。因此,微积分课程已成为理工类大学生知识和能力结构的重要组成部分。

席卷全球的新经济的蓬勃发展对工程教育的改革和发展提出了新的挑战,新工科建设的提出正是对这一挑战做出的积极回应。随着信息技术的发展,互联网改变了人们获取知识的渠道和方式。信息化、数字化和智能化新形势给高等教育带来了新的挑战与活力。在大数据时代下,在新工科理念指导下,人才培养对于专业知识的应用化、个性化、多元化的学习需求越来越重视,而与传统教育模式、学习方式之间的矛盾日益加剧[1-3]。因此,教育信息化的变革将是势不可当的大趋势,科技信息化、教学实践化的不断渗透将给微积分课程学习产生重要影响,也将给微积分课堂教学带来新机遇和新挑战。尤其近几年,在新的专业布局优化调整下,高等院校对应用型科技大学本科专业全面实施专业建设论证,实施完全学分制改革,微积分课程面临学分比例大幅度减少的新趋势。面对强大的社会环境和教育环境的冲击,微积分教学工作面临前所未有的挑战。对我校来说,办学定位是职业导向的高等教育,人才培养目标是技术应用型人才,那么微积分教学工作如何服务好我校工科类人才培养目标？如何适应微积分课程学分比例减少而教学内容不减的教学改革？如何满足学生们个性化、多元化和专业应用性的学习需求？为了解决这些问题,教材配备必须适应信息时代特点,教学方法必须结合信息时代特征。因此,我们需要更加配套、更加科学的微积分课程体系、课程内容、教学方法和考核模式,提高课堂45 min的教学容量和质量。

本文主要探索如何将微积分课程体系重构及教学内容改革,为学生提供更加适合的课程知识体系和教学内容,并应用于课堂教学,充分发挥学生学习的主体地位,变被动学习为主动学习,使微积分课程满足工科学生专业特征和个性发展的需要,激发学生学习的兴趣,有效提高学生运用数学的能力。

1 课程体系重构

传统的微积分教材是将一元微积分放在教材上册(课时数96),而将多元微积分、解析几何、无穷级数、微分方程等知识放在教材下册(课时数80)。针对我校工科微积分课程“64学时+64学时”的学时分配方案,原有的课程体系需要重新架构。在新的课程体系中,我们将微分学和积分学这两大知识体系分开,课程体系重新设计为:预备知识、极限部分、一元函数微分学、多元函数微分学等4大块知识结构等放在教材上册,并在秋季学期完成该教学内容。而将一元函数积分学、多元函数积分学、微分方程和无穷级数等4大块知识放在教材下册,并在春季学期完成该部分教学内容。在预备知识部分,我们将函数的基本性质、复合函数、集合概念和空间解析几何等知识都放入其中,让学生集中学习这些预备知识,充分掌握一元和多元在空间图形上的直观表现,为后续的一元和多元微分学、积分学知识打好基础。这样完全崭新的架构设计,不同于其他同类微积分教材的架构,具体架构对比见表1。这个新设计不仅在微积分课程知识点衔接上更加紧密,而且学生在学习过程中感觉更加自然连贯。在教学过程中更加有利于学生理解、记忆和掌握,从而大大提高了学生学习知识的连贯性和兴趣性。

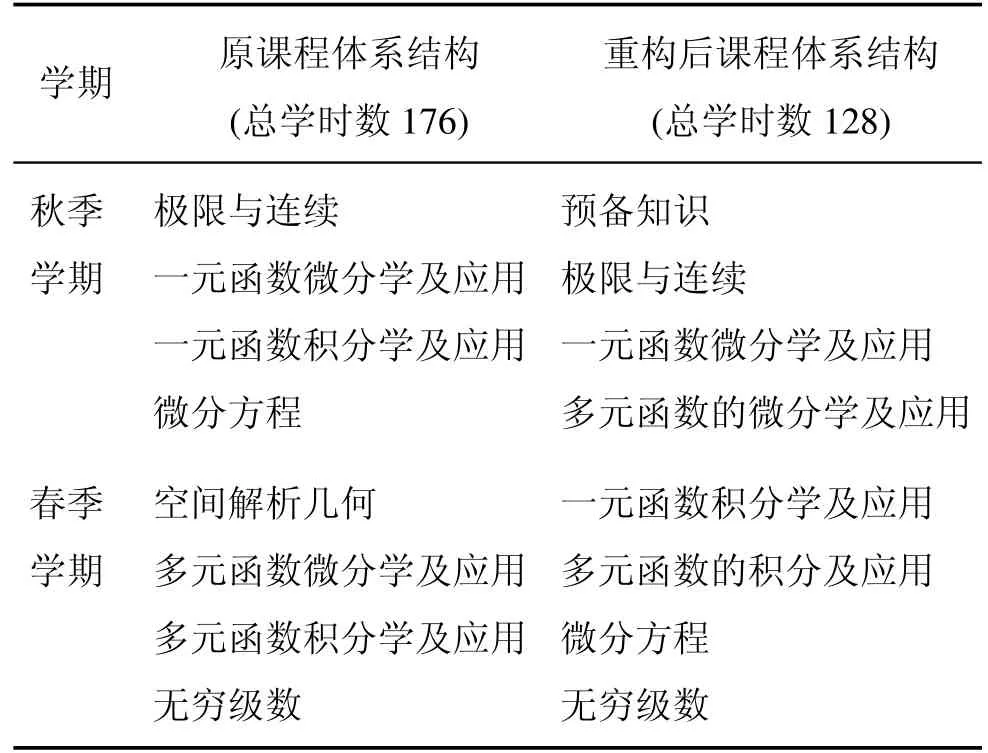
表1 微积分课程体系重构前后知识结构对比Tab.1 The comparison on structure of knowledge before and after the reconstruction of calculus curriculum system

2 课程教学改革

2.1 教学内容结合课时分配

针对我校工科专业微积分课程课时锐减(176→128)的基本现状,课程理论知识内容的教学改革势在必行。由于微积分课程具有知识点多、理论性强、知识点衔接紧密的重要特点,课堂教学中的每一个教学内容、每一堂课都有新的知识点不断渗入,因此要求学生在学习过程中,尤其是学生的听课过程,专注度要高,紧迫感要强。为了有利于学生对知识点的掌握,并做到学以致用,我们在教学内容改革上不断深入研究,探讨易于学生接受的微积分教学方法、特别是有重要应用价值的微积分知识。比如,极限的概念,是贯穿微积分课程始终的一个重要理论知识点,此概念理论性强、抽象程度高。学生在学习过程中常常感到晦涩难懂,尤其函数极限的概念。那么在教学过程中,我们要采取由易到难、由直观到抽象再到直观这样一个循环的过程,逐步渗透到课堂教学过程中,帮助学生理解这一概念。教学内容的把握上,可以从数列极限开始逐步过渡到函数极限概念。把数列极限的概念详细讲解,让学生对这一概念(即ε-N 概念)吃透,然后进行推广和抽象,逐步过渡到函数极限,再利用几何图形,让学生在直观中去感受函数极限的概念。如:的直观教学可以参考图1中相应的图形,而不必再局限在函数极限ε-δ的理论概念中不能自拔。而这一教学内容的改革思想在我们新编制的讲义里和课堂教学中都要很自然地体现出来。让学生真正做到好理解、好掌握、好应用。在课后练习部分,给出了两个习题模块:A基础题,B综合题。其中,模块A基础题部分,属于学生必须掌握的基础知识和微积分计算方法;模块B提高题部分,主要是针对学生专业要求和考研要求的提高知识,部分章节补充有实际建模应用题,有利于帮助学生拓宽微积分应用能力。

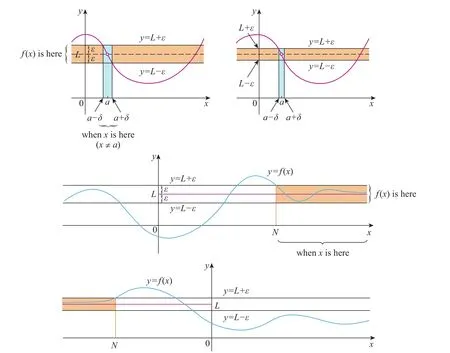
图1 函数极限几何表示图Fig.1 The geometric graph of functional limit

2.2 教学方式结合时代特征

互联网改变了获取知识渠道和方式,教学方式必须结合信息时代的特征。人们愿意在更加自由、灵活和宽松的环境下获取知识或者补充学习,因此课堂教学和课后自主学习的教学方式缺一不可,课堂教学为主与课后自主在线学习为辅相结合的混合式教学模式是当前信息时代的要求。为了实施这一混合式相结合的教学模式,方便学生自主补充学习,我们将微积分课程教学内容全部制作视频,上传课程中心,供学生在线辅助自主学习使用;并录制部分习题课视频和部分重点知识学习的微课教学视频,上传课程中心,让学生可以有所选择地补充学习课堂教学中没有“吃透”的知识点和解题过程中难以掌握的解题技巧和解题方法。将微积分在线课程的优质资源应用到教学和学生自主学习中,分步骤、分阶段地来研究并改善课堂教学模式,以适应学生学习时间和学习方式的灵活性,有效培养学生的个性化和多元化。

2.3 人才培养结合多元化社会需求

新经济的蓬勃发展对工程教育的改革和发展提出了新的要求、新的挑战,对多元化人才的需求愈加迫切，因此新工科建设的提出正是对这一挑战做出的积极回应。随着社会的发展,产业结构不断变化,新的经济模式不断涌现,这些都离不开多元化人才的培养,对人才结构和素质培养提出了新的要求。大数据、新能源、智能制造、生物健康等需要多元化的交叉学科人才。而微积分知识是培养数学人才和其他工程及经济领域优秀人才必须具备的基本技能和基本数学素养,因此在微积分课程教学过程中,我们一方面要重视微积分理论知识、计算方法,更要注重微分积分知识结构的应用性训练,体现理论联系实际[7-9]。比如在讲授导数的知识的时候,针对部分工科专业,不妨补充电容器电量充电问题的应用案例;在讲授函数的极值的时候,可以补充工程设备费用最省、市场利润最大等不同问题的案例内容;在讲授积分内容时可以补充放射性物体放射物的总量、不规则钢体容量等应用问题的实例[4-6]。在空间解析几何部分,不妨以课堂演示教学的方式指导学生如何利用数学软件制作三维图形,从而对立体图形、旋转曲面等知识有个初步、直观的理解[10],培养学生的数形结合思想。充分体现理论与数形相结合、理论与实际相结合的教学理念,培养学生多元化综合知识运用的能力,以便学生更好适应多元化社会需求。

3 结 语

总之,大数据时代多元化应用型人才的培养是时代赋予我们的使命。而多元化应用人才的培养离不开多元化师资队伍的建设。在教学工作中,需要建设“数学+”型师资团队,即团队中的每个老师需要将自身的数学知识应用到某一应用型研究领域,充分发挥实际问题中的数学支撑作用。而我国几十年来应用数学教师的培养基本沿着基础数学教师队伍建设的思路,我们需要在实践教学和研究中不断打破这一传统思路,逐步加强教师队伍对新工科教学理念的认知,并根据我校工科专业对微积分课程教学内容的客观要求,积极开展教学内容的改革实践。让教师尽快聚焦大数据、新工科时代下大学数学课程教学的关注点,尽快提升应该具备的多方位教学能力。目前我校正在通过试点专业(机械电子工程、自动化、网络工程、机械工程)微积分课程结构新体系的教学实践,把青年教师的教学研究兴趣引导到解决工程实际问题的交叉领域教学中来,培养教师的数学建模能力、组合优化能力和数据分析能力,打造“数学+”型教学团队,让学生在新的课程结构体系中充分感受“微积分+应用”的知识魅力。同时,通过对“数学+”型师资队伍的培养,提升团队教师多元化教学能力,为我校多元化应用型人才的培养做出应有的贡献。