爆炸冲击作用下金属圆柱壳体膨胀破碎过程研究

郭光全,朱建军,姚文进,李文彬

(1.晋西工业集团有限责任公司,山西 太原 030027;2.南京理工大学 智能弹药技术国防重点学科实验室,江苏 南京 210094)

圆柱壳体结构是战斗部中应用最广泛、最具有代表性的典型结构之一,而爆轰加载下金属圆柱壳体膨胀破碎过程问题早在20世纪70年代就得到了研究学者的广泛关注,如Taylor[1]首先提出了壳体在高应变率加载下动态断裂应力准则,Hoggatt[2]提出装药爆轰赋予柱壳的应力状态直接影响柱壳的塑性变形行为和破碎模式表现。在炸药作用下圆柱形金属壳体向外不断加速运动,由于炸药爆炸过程中产生的气体产物压力非常高,壳体在极短的时间内快速膨胀最终破裂形成破片,因此对圆柱壳体在爆轰产物作用下运动过程的研究显得十分重要。前期俄罗斯学者就提出了欧拉坐标系中不可压缩刚塑性壳体的一维膨胀运动模型[3],基于物理模型的建立来表征壳体的加速、变形以及破碎过程。Chou等[4]将指数加速模型用于描述柱壳在内部爆炸加载下的驱动加速过程。国内外学者采用不同的模型来描述爆轰产物膨胀与壳体材料行为变化过程,但本质上都是以能量的角度为出发点进行研究。另外,随着测试技术的发展,文献[5-6]利用试验方法获得了金属柱壳表面从膨胀、裂纹萌生到爆轰产物泄漏的演化图像,研究了高应变率下早期裂纹萌生及扩展的动态演化过程。国内任国武等[7]采用高速分幅相机和多普勒探测系统阵列联合测试了钛合金柱壳在内置炸药加载下膨胀、断裂直至整体破碎的表面动态图像。然而,爆轰加载过程中柱壳动态膨胀破碎过程远比单纯材料失效问题复杂,对其运动初期的响应,爆轰产物膨胀,裂纹萌生及扩展过程了解还相对较少。另外,对起爆时序以及稀疏波的影响而导致的壳体外壁轴向各处变化规律不一致的研究也较为少见。

本文基于拉格朗日动力学理论,建立了柱壳装药结构内爆加载下金属壳体膨胀运动过程分析模型,分析了轴向不同位置壳体的膨胀规律,并利用超高速摄影试验装置获得了压装CL-20基混合炸药的40CrMnSiB圆柱壳体在爆轰加载下的动态膨胀及断裂过程。

1 高应变率下壳体膨胀变形过程理论分析

对柱壳装药结构在高应变率下壳体结构膨胀断裂过程的全面认识一直是一个难题,为了有效计算壳体内部任意处膨胀运动参数,本文基于拉格朗日动力学理论,分析炸药与壳体的相互作用;采用爆轰过程中能量转变理论推导爆轰产物驱动壳体的膨胀过程。

为了建立壳体运动方程,本文做如下假设:①假设壳体轴向方向无限长,忽略轴向爆轰产物的泄漏作用,只考虑壳体的径向运动;②壳体材料不可压缩,整个运动过程中壳体材料密度不变;③在装药爆炸推动壳体膨胀的过程中,由于作用时间很短,忽略变形所存储的能量,炸药释放的能量转化为壳体以及炸药的动能。图1为研究所用模型示意图,图中,r10,r0分别为壳体初始时外半径和内半径;r1,r分别为圆柱壳体运动过程中任意时刻的外壁半径和内壁半径。

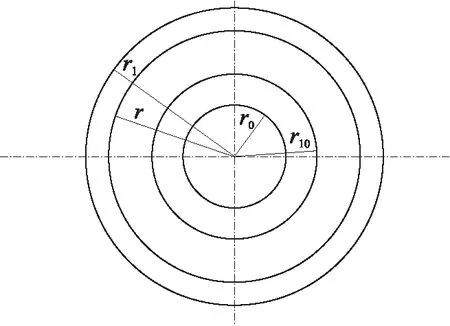
图1 模型示意图

由假设①和假设②可知,壳体满足质量守恒定律和材料不可压缩假设条件,有关系式:

ρm=const

(1)

(2)

式中:ρm为壳体材料密度,Δ0为常数。

对于不可压缩壳体,由假设③可知,壳体运动过程较为短暂,前期作用过程中壳体变形所储存的能量可以忽略。依据Lagrange形式运动方程,壳体运动过程满足[8]:

L=T-U

(3)

(4)

式中:r为壳体内半径;L为Lagrange函数,是系统动能和内能之差;T为爆炸过程中总动能;U为总内能。另外,由平面假设条件①可知,壳体在爆轰驱动运动过程中,炸药释放的能量转化为炸药和壳体动能[9],因此单位长度内动能T满足:

(5)

式中:第1项表示壳体动能积分,第2项表示炸药气体动能积分;mat即代表对壳体整个质量的积分,m1为单位长度壳体质量;gas表示炸药气体质量的积分,m2为单位长度炸药气体质量;v,vgas分别为壳体及爆轰产物气体速度。一般条件下可认定壳体运动过程中炸药及爆轰产物运动速度沿径向均满足线性规律:

(6)

vrr=viri=c(t)

(7)

式中:vgas(x)为距中心x处爆轰产物速度;vr为壳体内壁速度;vi,ri分别为壳体内任意处速度及半径;c(t)为只与时间相关的变量。

联立式(5)、式(6)及式(7),可求解动能:

(8)

式中:m1,m2分别为单位长度壳体及炸药质量,即

(9)

式中:ρ0为炸药密度。

壳体膨胀过程中单位长度的爆轰产物内能为[8]

(10)

式中:pr为任意时刻爆轰产物压力。

假设高压爆轰产物在壳体膨胀运动过程中进行绝热膨胀,且绝热指数γ在膨胀过程中保持不变,则有关系式:

pr=p0(V0/V)γ

(11)

(12)

式中:p0,V0分别为炸药爆炸时的初始压力和体积,在实际爆轰过程中,点起爆下爆轰波阵面压力达不到壳体CJ爆压,因此本文初始压力可取爆轰波阵面压力的3/4;V为膨胀过程中爆轰产物体积,将式(11)、式(12)代入式(10),可求解出单位长度的爆轰产物内能:

(13)

联立式(2)、式(4)、式(8)及式(13)可求得壳体内壁运动方程:

(14)

通过式(14)可以求出壳体内部膨胀速度以及膨胀半径随时间的变化规律。另外,联立式(2)、式(7)、式(14)可求解获得壳体内部任意处运动方程。

2 壳体膨胀变形过程试验验证

2.1 试验设计

为了验证本文所建立的计算模型,设计了圆柱装药壳体静爆试验,利用超高速摄影试验拍摄壳体在爆炸加载下膨胀断裂过程。试验现场布置如图2所示。

图2 试验布置图

圆柱装药结构如图3所示,其中炸药装药为CL-20基压装混合炸药[10],装药长度为80 mm,直径为50 mm,壳体材料选用40CrMnSiB合金钢,壳体壁厚为6 mm。壳体两端盖高为10 mm,采用螺纹连接方式,连接部分长度为5 mm,选用45#钢作为端盖材料。起爆方式为圆筒一端中心起爆,战斗部总长为90 mm,外径为62 mm,壳体材料性能参数见表1,表中,σb为抗拉强度,σs为屈服强度,δ为断裂韧性。

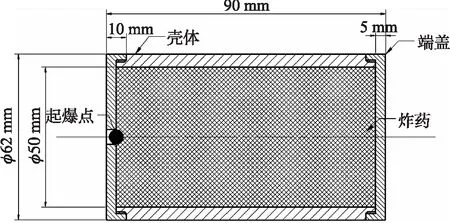
图3 战斗部结构图

利用SIM型超高速摄影仪拍摄壳体在爆炸加载下膨胀断裂过程,拍摄帧频最高可达6×106s-1,综合考虑图像的清晰度与对比度,将高速摄影仪的曝光时间设置为5 μs,每2幅图像间的时间增益为1 μs。

2.2 试验结果及分析

试验获得了壳体在0～40 μs之间的动态变形过程,表2给出了部分时刻超高速摄影图像。由表2可知,在上端面中心起爆条件下,由于壳体两端约束较弱,爆轰产物从两端泄漏较大,且根据爆轰产物沿轴向传播的时序性,壳体外表面各处动态变形情况并不一致。选取壳体外表面距起爆端距离分别为20 mm,40 mm,58 mm,65 mm的D1,C1,B1,A14个点作为观测点进行研究,在膨胀初期距起爆端较近的D1,C1两处先开始膨胀,因此其膨胀距离以及速度均大于B1,A1两处;随着膨胀的进行,爆轰产物不断泄漏及轴向稀疏波作用导致D1,C1两处膨胀速度增加幅度逐渐减缓,而B1点附近壳体受爆轰产物泄漏影响较小,爆轰产物作用于壳体内壁的压力能较好地维持,使得其受爆轰产物作用最强,这导致后期壳体膨胀距离大于D1,C1两处。

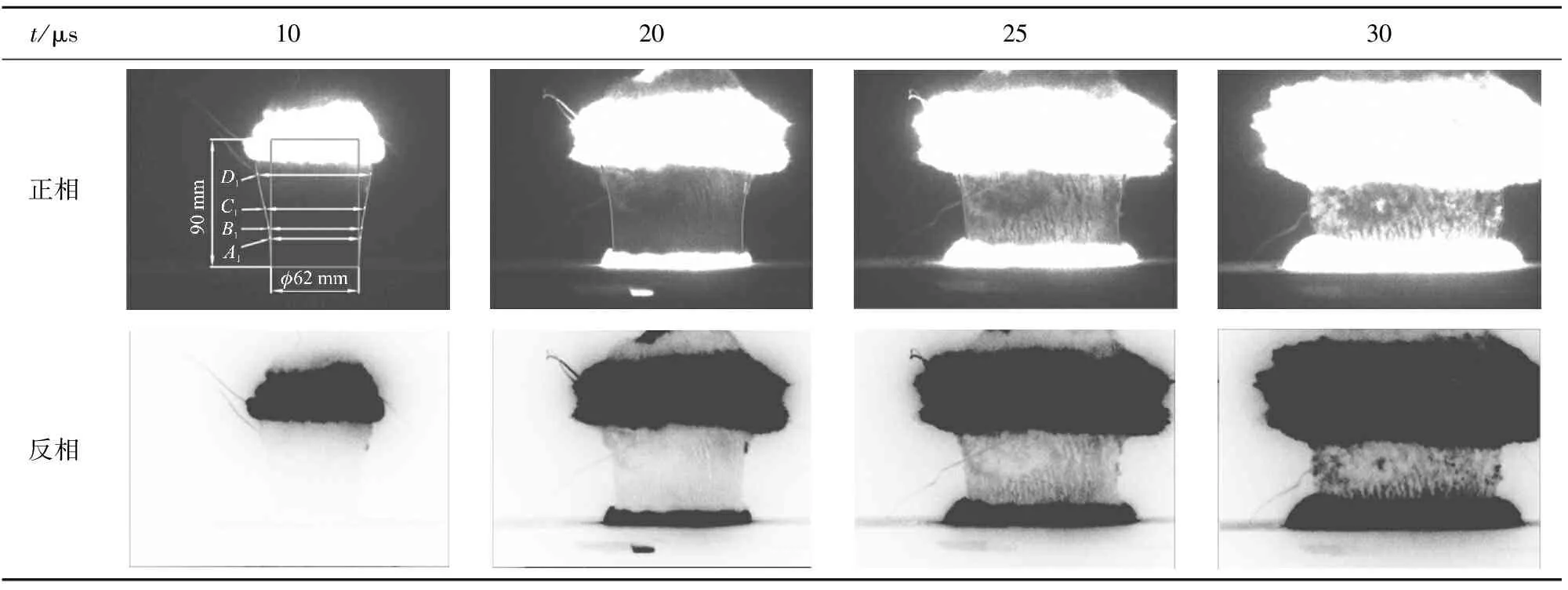
表2 40CrMnSiB钢壳体动态变形过程部分结果

通过图像处理软件Hornil-StylePix对高速摄影图像按像素点进行标定,图4为30～35 μs期间壳体外壁平均膨胀速度vt沿轴向分布规律,图中,l为距起爆端的距离。由图可知:壳体外壁沿轴向不同位置处膨胀速度并不一致,其中测点B1附近径向膨胀速度最大,约为1 656 m/s;而测点D1处,由于起爆端附近爆轰产物泄漏十分严重,轴向稀疏波影响较大,导致膨胀速度比B1处小15.6%;非起爆端附近测点A1处,爆轰产物泄漏程度低于起爆端,受稀疏波影响较小,使得测点A1处膨胀速度比D1处大9.8%。壳体径向膨胀速度在距起爆端60%～70%壳体轴向长度处达到最大。壳体膨胀速度从起爆端沿轴向先上升后下降,且起爆端附近的破片速度低于非起爆端的破片速度。

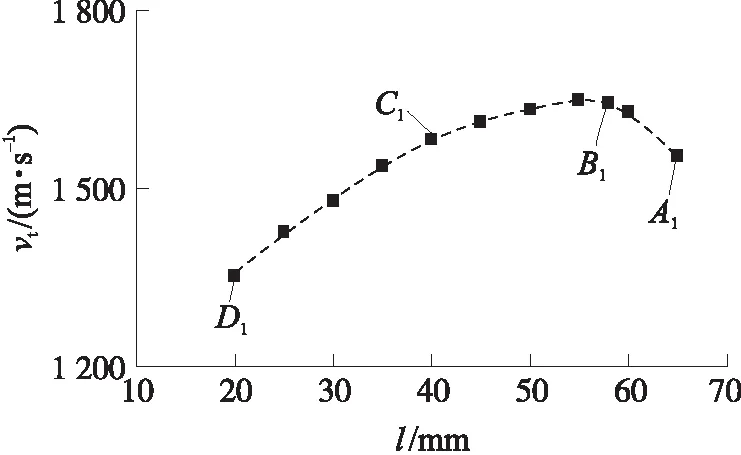
图4 轴向不同位置壳体外壁平均膨胀速度

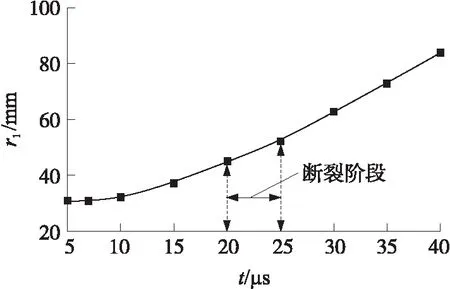
图5 测点B1处膨胀半径随时间变化规律

3 理论模型与试验结果的对比

利用本文所建立的理论模型对柱壳装药结构的膨胀过程进行了计算,并与测点B1处壳体径向膨胀半径随时间的变化试验结果进行对比,如图6所示。理论所得结果表明:随着时间的推移,壳体内、外壁之间距离不断减小,且在壳体膨胀初期,理论计算所得壳体膨胀半径与试验值变化趋势一致,误差在5%以内;而随着膨胀的继续,在20～25 μs之间,观察到壳体开始破碎,壳体内部所受自身约束作用逐渐减弱,爆轰产物作用逐渐作为唯一驱动力,壳体断裂逐渐形成破片且不再发生变形,壳体在爆轰产物作用下继续加速沿径向飞散,试验所得膨胀速度增大,导致试验结果与理论值差值逐渐增大,此后模型不再适用。

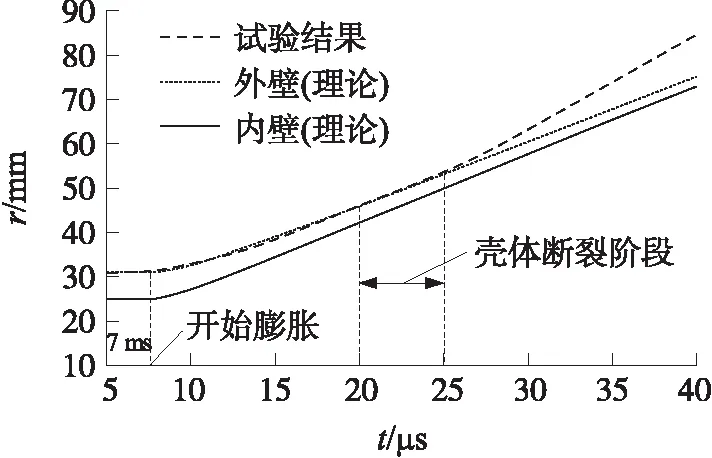
图6 壳体径向膨胀距离随时间的变化规律对比

4 结论

①超高速摄影试验获得了高应变率下40CrMnSiBi钢圆柱壳体膨胀断裂破碎过程。壳体膨胀破碎过程可分为3个阶段,包括壳体膨胀初期裂纹萌生阶段,壳体内部裂纹扩展、贯穿至整个壳体厚度阶段,以及爆轰产物泄漏、断裂形成破片前期阶段。研究发现膨胀半径达到1.47～1.70倍初始外半径时,壳体内部裂纹贯穿整个壁厚并发生断裂。

②试验发现了轴向不同位置壳体外壁平均膨胀速度变化规律,壳体膨胀速度从起爆端沿轴向先上升后下降, 在距起爆端60%～70%壳体轴向长度处达到最大,且此处膨胀速度比起爆端附近提高了18.3%。

③基于拉格朗日动力学理论分析了炸药与壳体的相互作用过程,建立了内爆加载下金属壳体内部膨胀运动过程分析模型,理论计算结果与试验结果较吻合。