无再入观测弹道导弹气动参数和落点联合预报

吴 楠,王 锋,孟凡坤

(信息工程大学 数据与目标工程学院,河南 郑州 450001)

弹道导弹落点预报是导弹预警系统中的一个重要环节,落点预报精度是预警雷达的重要技术指标,提高落点预报和误差分析精度具有很强的工程意义[1-2]。提高落点预报精度的关键是建立准确的预报模型[3],如孙瑜等[4]建立了考虑地球J2摄动的弹道预报模型,潘晓刚等[5]建立了考虑J4摄动的弹道预报模型,但这2种方法均没有考虑导弹再入时所受气动阻力的影响。由于再入气动阻力是影响落点预报精度仅次于地球自转的因素[6],较多的研究方法是在再入过程中通过引入观测数据快速地辨识气动参数,然后再用于落点预报,如陈映等[7]利用交互多模型方法估计弹道系数,史金光等[8]建立了气动复合系数模型并借助扩展卡尔曼滤波进行辨识,赵捍东等[9]借助观测数据用径向基函数神经网络逼近弹道方程,张金凤等[10]将再入状态估计和弹道系数辨识进行联合优化,均进一步提高了落点预报精度。然而在导弹的早期预警阶段,由于导弹并未再入,无法获得再入观测数据,且气动参数信息也无法预先准确获知,此时如何考虑再入气动的影响,并建立高精度的落点预报和分析模型是研究的难点。

本文在无再入观测数据条件下,基于弹道导弹打击目标时对终端速度变化范围的限制,反推出气动阻力参数的变化范围,然后将气动阻力参数作为随机过程建模,并增广为目标的状态,建立考虑气动阻力、地球自转和J2摄动的高精度落点预报方程,采用数值积分和无迹变换的方法对落点经纬度和落地时刻进行预报和误差分析。

1 考虑气动阻力的导弹落点计算方程

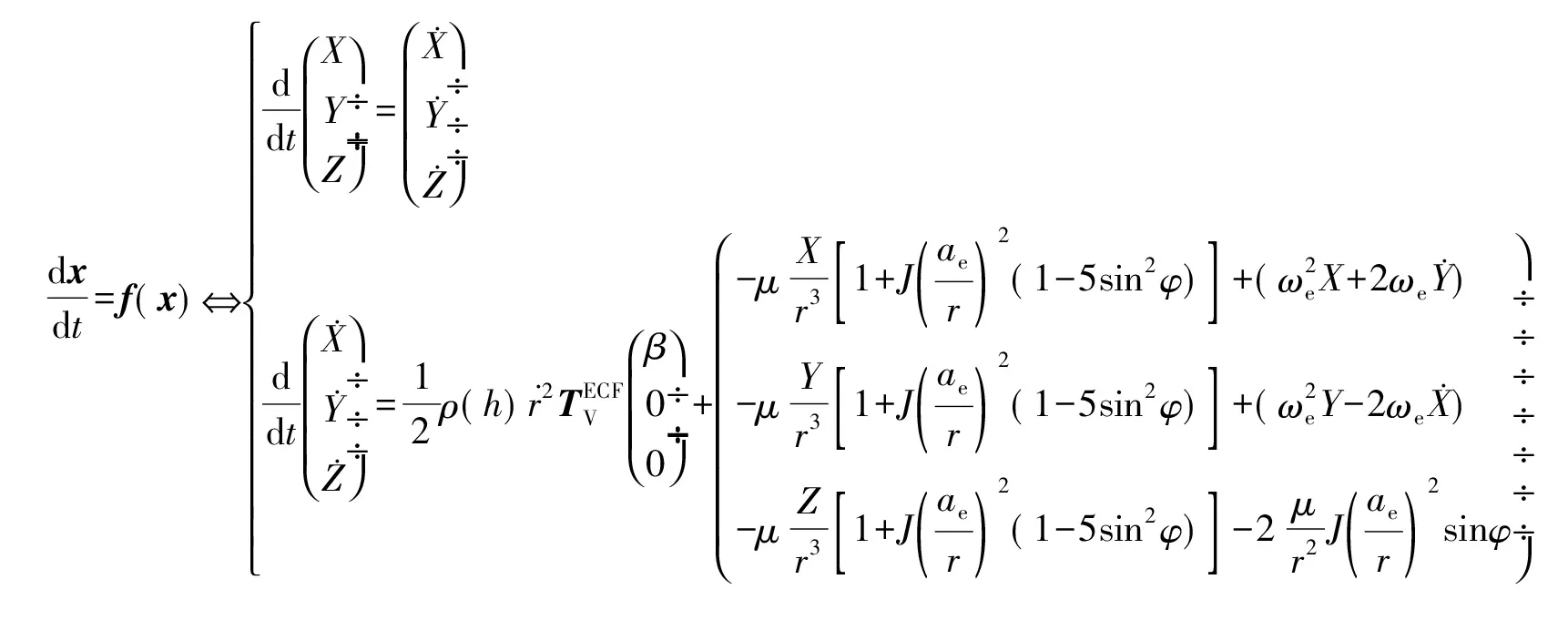
(1)

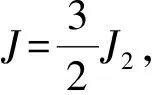
(2)

(3)

(4)

2 气动阻力参数变化范围预估

(5)

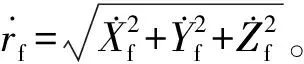
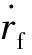
(6)

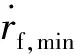
(7)

(8)

式中:δβmax(k)为相对于βmax(k)的小量,可取为δβmax(k)=10-8βmax(k)。

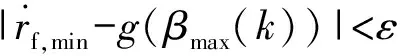
3 基于无迹变换的落点均值预报和误差传播计算

气动阻力参数是导弹的固有属性,具有确定性,但防御方无法获取该参数准确的变化规律,因此在弹道和落点预报时,只能将气动力参数作为随机量处理。假设用Wiener过程描述气动力参数[11],相应的气动阻力参数模型可表示为

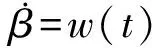
(9)

式中:w(t)为白噪声过程。将式(9)离散化,得:

β(k+1)=β(k)+wk

(10)

式中:wk为离散化驱动白噪声序列,方差取决于随机序列{βk}的分布模型。由于没有任何气动阻力参数的先验信息,且为了表征气动力参数的剧烈变化情况,假设气动阻力参数在变化范围内服从均匀分布,则气动阻力参数的均值为

(11)

方差为

(12)

(13)

当系统中含有随机量时,对其统计特性的分析方法有Monte Carlo抽样统计法和协方差分析描述函数法等,其中前者具有推导计算简便、结果直观可靠等优点,但缺点是耗时过长且结果不是精确解,后者则具有省时、高精度且便于理论分析等优点,但缺点是统计线性化过程过于繁琐,且要求系统模型全域一阶可微,当系统模型较为复杂且不满足可微性条件时,协方差分析描述函数法将不再适用。无迹变换(unscented transform,UT)是用于计算经过非线性变换的随机变量统计特性的新方法[12],UT不需要对非线性方程线性化,而是对状态矢量的概率密度函数进行近似,因此将UT应用于非线性随机系统的状态预报,与协方差分析描述函数法相比具有2个优点:①不需要求解Jacobian矩阵,不要求系统模型具有一阶可微性,算法更易实现,应用范围进一步扩大;②预报获得的后验均值和方差都能够精确到二阶,具有更高的预报精度。本节采用UT方法,基于再入段增广状态方程式(13),对考虑再入气动阻力的落点进行预报和误差传播分析。定义落点信息矢量z=(tfLfBf)T,利用式(13)和式(2)～式(4)可以获得落点信息矢量和初始增广状态矢量间的函数关系H(·):

(14)

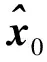
(15)

式中:O为零矩阵。利用UT进行均值和误差传播计算,首先基于式(15)构造2n+1个Sigma点和相应权重,对于本文情况,y0的维数n=7。

(16)

z(i)=H(χ(i))i=0,1,…,2n

(17)

最后利用统计的方法计算落点信息矢量的均值和协方差矩阵:

(18)

4 落点误差椭圆计算

(19)

然后将计算得出的误差椭圆旋转平移至大地经纬度平面。

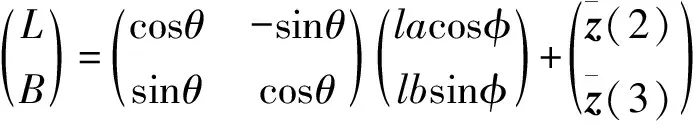
(20)

式中:φ∈[0,2π),l为标准差的倍数,通常取l=3(落入该误差椭圆的概率为97.3%)。

5 仿真分析

5.1 仿真条件设置

基于某雷达针对某型弹道导弹的探测数据,进行滤波和弹道估计,以滤波稳定时刻t0=540 s时的弹道估计值作为预报初值,此时时间为2011年3月7日8时53分19秒(协调世界时),状态矢量(地固系位置和速度矢量,单位分别为m和m/s)估计均值为

对应的估计误差协方差矩阵Px0为

表1 导弹的真实落点信息

5.2 未知气动阻力参数预估

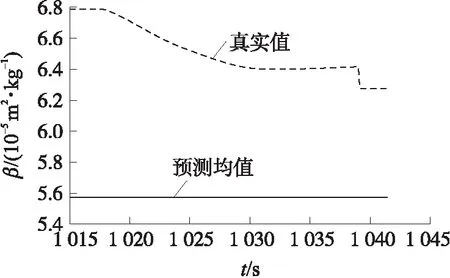
图1 气动阻力参数预测均值与真实值

从结果可以看出,再入过程中真实气动阻力参数是时变的,变化范围为6.2×10-5～6.8×10-5m2/kg,但变化幅度不是很大,且由于再入过程持续时间较短,所以将其作为常值进行近似处理是较为合理的,而本文基于先验信息预测获得的气动阻力参数均值与真实值相比,处于同一数量级,且相对误差约为10%,说明本文算法通过先验信息预测的气动阻力参数是较为准确而有效的。

5.3 落点预报误差分析

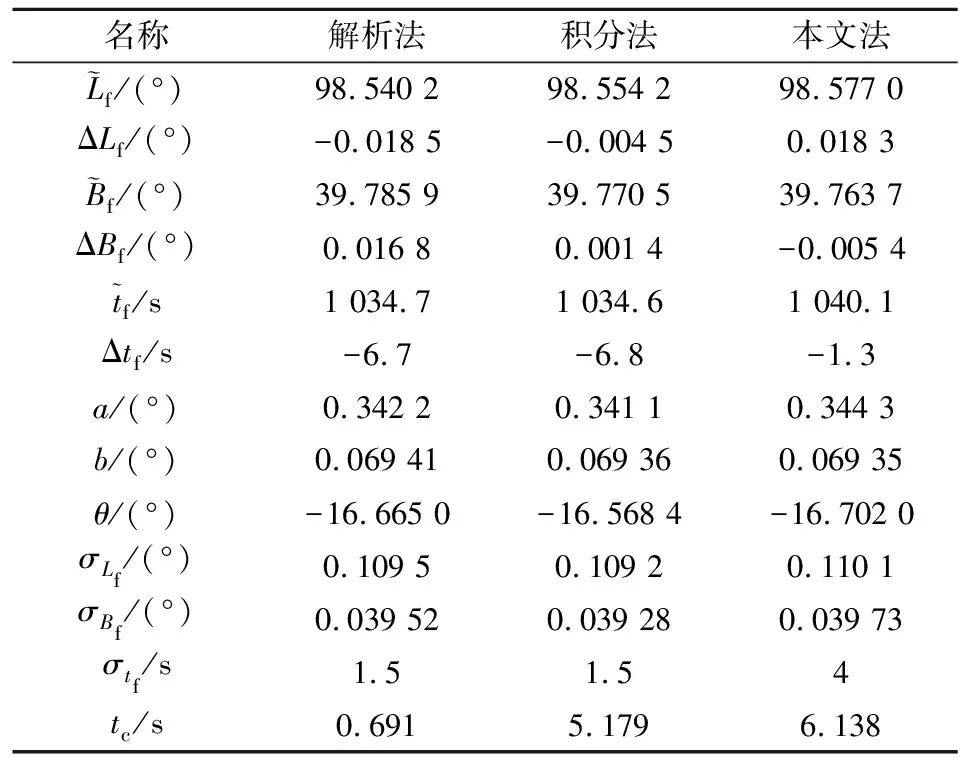
表2 3种方法落点预报结果比较

从计算结果可以看出:①解析法虽然耗时最短,约为其他2种算法的1/10,但是无论是落点还是时间预报精度都较差;②积分法落点预报精度较高,但由于其时间预报误差较大,造成时空不匹配,大大增加了落点预报误差;③本文算法耗时与积分法相当,由于考虑了气动阻力的影响而且对阻力参数进行了有效的预测,落地时间精度显著提高,所以时空匹配较好,具有较高的落点和时间联合预报精度;④本文方法预报时间的标准差要大于另2种方法,这说明当考虑了气动阻力参数后,再入段速度变化较为剧烈,导致导弹的预报落地时间具有较大的散布,较另2种方法与实际情况更为符合;⑤3种算法计算的误差椭圆大小和形状类似,椭圆的长轴(表征纵向标准差)近似沿射向方向,纵向标准差(长轴)显著大于横向标准差(短轴),前者约为后者的5倍,这是因为导弹飞行时速度纵向分量显著大于横向分量。与前2种方法相比,本文算法计算的误差椭圆纵向标准差(长轴)有所增加,这是因为考虑气动阻力的影响后增加了导弹速度纵向分量变化的不确定性,从而增大了落点纵向散布。

以Monte Carlo打靶仿真2 000次获得的落点散布为基准,分别与3种算法计算的误差椭圆进行对比,以验证算法的准确性和有效性,比较结果如图2所示。

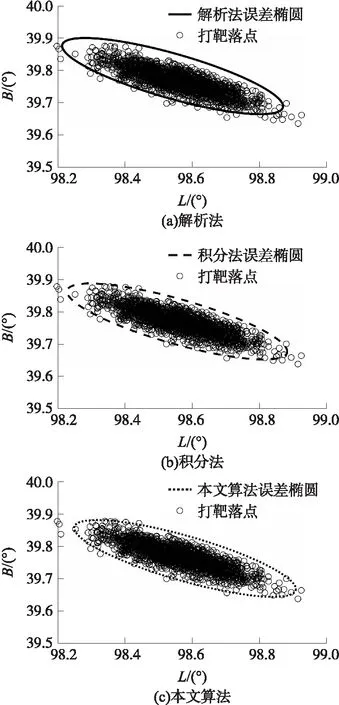
图2 打靶(2 000次)落点散布与计算误差椭圆的比较

从结果可以看出:①解析几何法计算的误差椭圆精度最差,纵向和横向都存在偏差,纵向偏差是由于没有考虑再入气动阻力导致,因此整体向前偏移(实际落点由于受到阻力作用射程会更近一些),横向偏差则主要是没有考虑地球引力J2摄动影响导致;②数值积分法的误差椭圆精度优于解析几何法,由于考虑了地球引力J2摄动影响,横向偏差基本消除,但是由于没有考虑再入气动阻力的影响,仍然存在纵向偏差;③本文提出的考虑再入气动阻力模型法预报精度最高,与实际的打靶结果最为符合,这是因为该方法既考虑了地球引力J2摄动影响,又考虑了再入气动阻力影响,有效消除了纵向偏差和横向偏差。

同样,以Monte Carlo仿真打靶2 000次获得的落地时间散布为基准,分别与3种算法计算的落地时间均值和±3σ范围进行比较,如图3所示,图中,N为打靶次数。

图3 打靶(2 000次)落地时间与预测均值方差的比较

结合表2和图3可以看出,解析法和积分法的结果几乎相同,由于其预报时间均值显著小于真值,且标准差结果偏小(与实际不符),导致打靶结果几乎都超出其预报均值±3σ范围之外,这说明误差分析结果与实际统计特性不匹配,这是因为2种方法均没有考虑气动阻力的减速作用,导致预报的导弹落地时间均有所提前,从而带来更大的落点预报误差;而本文算法由于考虑了再入气动阻力减速的作用,预报的落地时间与打靶结果符合较好,预报均值与打靶均值较为接近(相差1 s),且打靶结果均落在其预报的均值±3σ范围以内,说明本文算法的误差分析结果与实际统计特性更为匹配,可靠度和准确度更高。

6 结论

在弹道导弹早期预警阶段,气动阻力参数对落点预报精度具有显著影响,但通常无法获知且无再入观测数据对其进行辨识。本文基于导弹末端速度变化范围的限制,有效地预估了气动阻力参数的变化范围,然后建立了考虑气动阻力、地球自转和J2摄动项的落点预报和误差分析模型,并计算了落点误差散布椭圆。仿真结果表明,与传统的解析法和积分法相比,本文方法由于有效地预估出气动阻力参数范围,落点预报精度尤其是预报时间精度显著提高,计算的误差散布椭圆与打靶结果最为吻合。对于导弹早期预警阶段的弹道和落点预报工作具有较好的应用价值。