远程变后掠翼巡航导弹多任务弹道设计及仿真
2018-10-09王旭刚王中原
王旭刚,陈 琦,王中原
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
有翼多任务战术巡航导弹是一种防区外发射、精确制导的自主飞行器。因其具有航程远、打击精度高、突防能力强等特点,受到了多国军事工业部门的重视。新型变后掠翼战术巡航导弹弹翼的后掠角可根据飞行状态变化,从而提高飞行效率,降低能耗,实现多任务飞行。
采用变翼技术的导弹,主要是利用大后掠角、小展弦比弹翼适合高超声速飞行,以及小后掠角、大展弦比弹翼适合亚声速飞行的特点,将导弹的弹翼设计为后掠角度或弹翼面积可变结构,从而使导弹在高速及低速飞行时都能维持良好的气动特性。
变翼技术在飞行器控制领域的应用重新引起国防工业部门的重视,变外形飞行器涉及的材料、结构、空气动力学、制造、飞行控制等领域得到了广泛而深入的研究[1-2]。文献[3]将变后掠翼技术应用于无人机设计,该无人机主要强调高速的攻击能力及低速低燃料损耗的巡航性能,该研究测试了这种变后掠翼无人机在高速大后掠角及低速小后掠角情况下的气动参数,指出变翼技术可带来低能耗、高效率和多任务特征。文献[4]研究了巡航导弹的多任务变翼飞行的气动特性、动力学建模及仿真。王江华等[5]进行了伸缩弹翼巡航导弹的气动外形优化;王旭刚等[6]研究了变后掠翼巡航导弹的动力学建模及控制问题;许兆庆等[7]研究了折叠弹翼展开机构,并开展了仿真及实验。文献[8-11]以变后掠翼航弹为对象,分别研究了采用自适应滑模控制理论的弹道跟踪问题,基于最优控制理论和粒子群优化算法的滑翔弹道优化设计问题,并开展了弹道仿真及分析。文献[12-13]研究了变后掠翼的气动特性及变后掠翼的规律。国内外研究资料表明,对于不同类型的变外形飞行器,目前在气动特性、材料及结构、弹道等方面进行了相关研究,本文在上述研究的基础上,针对变后掠翼巡航导弹的多任务和远距离飞行特性,立足工程实现,进行不同飞行阶段的弹道设计、分析及仿真,为远程变后掠翼巡航导弹的弹道设计提供设计方法和思路。
1 变后掠翼战术巡航导弹的飞行特点
飞行器低速飞行时,需要平直翼或者较小的弹翼后掠角;高速飞行时,需要较大的弹翼后掠角或者无弹翼。采用变后掠翼的巡航导弹,通过改变气动外形来适应不同的飞行速度,能够满足多任务战术需要。
变后掠翼巡航导弹飞行过程可分为5个阶段:
①爬升。在安全区域,由飞机、舰船等进行空中或面发射,导弹迅速爬升到指定的巡航高度。
②巡航。爬升段结束,导弹在指定高度进行巡航飞行,导弹高速飞行,直奔作战区域。
③下滑。进入指定区域,导弹由巡航状态转入下滑段,完成降低高度的下滑飞行,在此过程中弹翼后掠角减小,导弹气动外形配合速度的变化。
④盘旋。导弹在战场上空盘旋,完成侦察任务,并可以等待控制中心的命令。
⑤俯冲。接到打击命令(或者打击默认目标),此时导弹增大后掠角,以大后掠角高速飞行,进行快速精确打击,保证打击的强度和有效性。
2 主要飞行阶段弹道
2.1 纵向爬升、下滑程序弹道
导弹采用程序高度来实现爬升和下滑的控制。为了使导弹实现快速平稳的高度变化,并顺利转入巡航和盘旋阶段,采用指数形式的纵向高度弹道,并根据程序高度信息和实际弹道高度,输入导弹制导系统,控制导弹按照程序高度飞行。
导弹爬升段的程序飞行高度表达式为
(1)
式中:K1为控制常数;h1,h2分别为爬升段初始和结束高度;t1,t2分别为爬升段开始和结束时间。
导弹下滑段的程序飞行高度表达式为
(2)
式中:K2为控制常数;h2,h3分别为下滑段初始和结束高度;t2,t3分别为下滑段开始和结束时间。
为了保证各个阶段的连接段的平滑,需要根据导弹的过载能力及飞行速度协调各个阶段的飞行时间及系数K1,K2的值,保证在变高飞行过程中的超调量小,转入平飞的时间短,变高过程中的导弹所承受的过载小于最大允许过载。
导弹在铅垂面内的质心运动方程为
(3)
式中:m为导弹质量;v,θ,x,y(或h)分别为导弹飞行速度、弹道倾角、射程、弹道高;FP,Fx,Fy分别为导弹受到的推力、气动阻力和升力;ny为过载。
导弹的速度为长周期运动,弹道倾角为短周期运动,过载也为短周期运动,因此在考虑每一时刻的制导过载指令时,可认为速度v是不变的,根据式(3)可得飞行过程中指令过载表达式:
(4)
式中:ny,c为指令过载。
根据式(1)及式(2)可得:
(5)
式中:K为K1或K2;Δh为h2-h1或h3-h2。
根据式(5)可得:
(6)
ny,max=(Δh)K2/v+1
(7)
设导弹能够提供的最大过载为np,则需要导弹在程序飞行过程中满足:
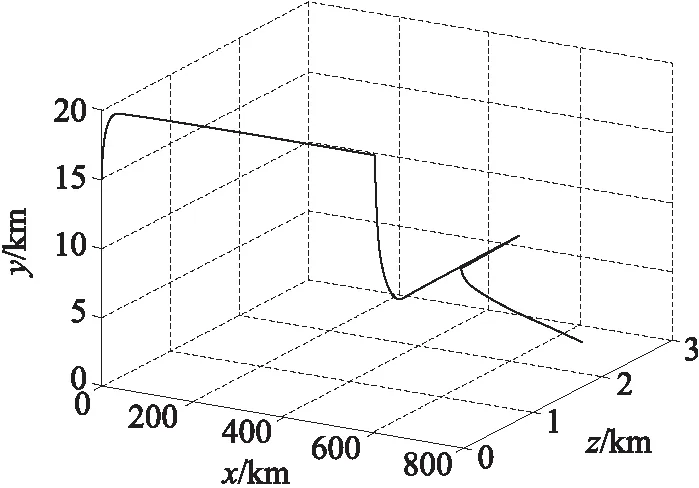
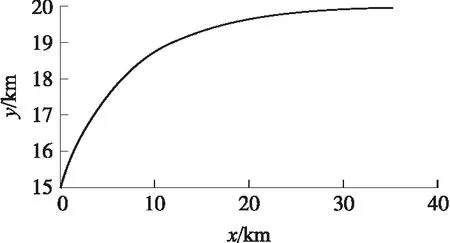
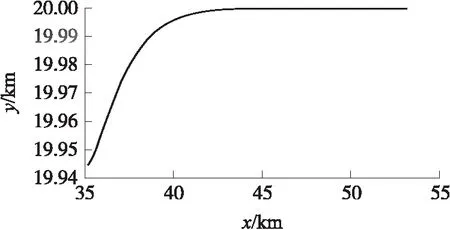
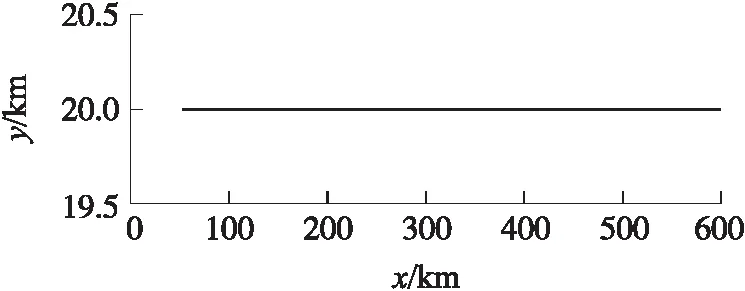
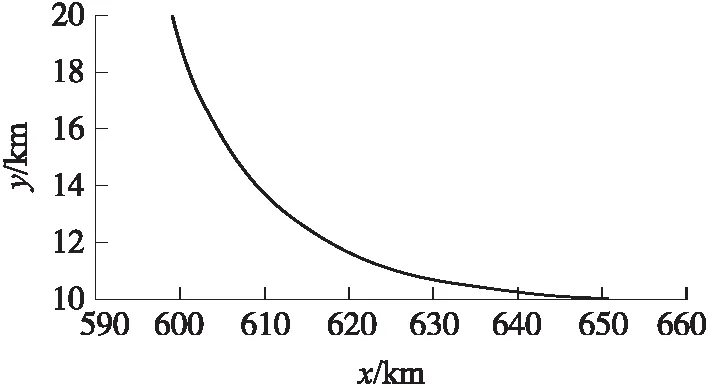
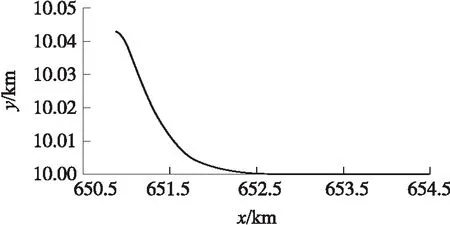
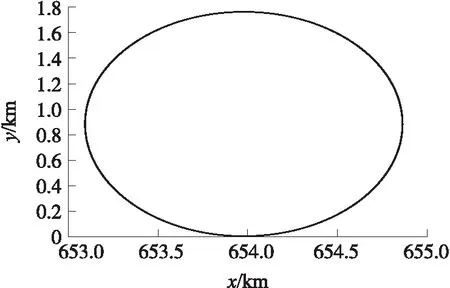
ny,max=(Δh)K2/v+1 (8) 根据式(8)可求出K的取值范围: (9) 根据式(9)可以估算K的取值。当选择K以后,就已经决定了导弹的弹道曲线。这里还存在爬升或下滑的时间段选择问题,即决定爬升与下滑段的飞行时间t。如果时间过短,则导弹向平飞段过渡的弹道就非常弯曲,导弹的需要过载就大,甚至可能会超出导弹能够提供的过载。导弹向平飞过渡初始时刻的导弹高度为 hc=(Δh)e-K(t-t*)+h (10) 式中:h为最终平飞高度h2或h3,t*为t1或t2。 在初始过渡阶段的导弹过载信号最大为 ny,c=k0(Δh)e-K(t-t*) (11) 式中:k0为导弹高度回路控制器输出与输入信号(高度误差)的增益。 为了保证过渡阶段对导弹的有效控制,需要|ny,c|<|np|,则根据式(11)可得: (12) 式(9)和式(12)给出了导弹爬升段和下滑段的程序高度表达式系数的取值范围,且均以导弹能够提供的最大过载为界限,所以K取最大及t取最小表示导弹以最大能力快速爬升,耗时及射程均最短。在具体选择时,可根据导弹飞行各段的时间和弹道要求进行调整,选择合适的K及t。 根据实际弹道和设计好的方案弹道程序高度,生成导引指令,引导导弹沿着方案程序高度飞行。 导弹飞到指定区域后,将会进入盘旋阶段,进行地面探测或等待控制中心的进一步指令。这时候导弹的纵向通道实现等高飞行控制,导弹的侧向通道实现围绕战区做圆形盘旋飞行。 导弹的弹道曲率半径与导弹的过载有着直接的关系。如果导弹在水平面内运动,则弹道上某点的曲率就是该点处的弹道偏角φv对弹道弧长s的导数,即 (13) 式中:κ为某点的曲率。 该点的曲率半径ρ则为曲率κ的倒数,可得: (14) 导弹在等高平飞段,纵向弹道倾角θ=0°,导弹的弹道偏角φv与侧向过载nz存在如下关系: (15) 将式(15)代入式(14),可得: (16) 由式(16)知,在给定速度情况下,侧向过载越大,则曲率半径越小,在该点处的弹道就会越弯曲,导弹盘旋覆盖的区域就越小。受到侧向最大过载的限制,导弹能够覆盖的最小区域半径为 (17) (18) 导弹平飞段采用等高飞行,方案弹道为直线弹道,根据方案高度和实际的高度差,输入高度控制器,产生过载指令,操纵弹体产生与重力方向相反的法向力。导弹等高飞行的高度控制器常采用经典超前校正补偿器,其一般形式为 (19) 式中:ny,pc为等高飞行制导指令过载;Kp,a,b为控制器参数,且满足0 攻击段为采用导引头的自动寻的制导,采用经典的比例制导,输出指令过载,其一般形式为 (20) 式中:ny,gc为攻击段制导指令过载,Ka为导航比,R为弹目距离,q为弹目视线角. 导弹由15 km高空进行本文设计的程序制导,经过爬升、20 km巡航、下滑、10 km盘旋及攻击,总航程为655.8 km,导弹巡航距离近似为600 km,初始质量为1 000 kg,盘旋终止质量为400 kg。从攻击到地面目标,在地面射向坐标系Oxyz内,整个飞行弹道如图1所示。地面射向坐标系的原点O为发射点,Ox轴指向射向方向,Oy轴沿着垂直面向上,Oz轴与Ox轴和Oy轴构成右手坐标系。 图1 导弹飞行全弹道 下面对主要飞行阶段进行分析及说明。 ①爬升段。 0~30 s,导弹进入爬升程序制导,导弹初始质量为1 000 kg,燃料消耗为2 kg/s,导弹飞行速度Ma=4,仿真结果如图2所示。选择的制导指令参数K=-0.15。导弹弹道平缓上升,导弹最大过载为4.5。爬升段结束时导弹质量变为940 kg。 ②巡航段。 30~500 s,导弹转入巡航阶段。此阶段导弹的初始质量为940 kg,发动机燃料消耗为1.05 kg/s,导弹速度维持在Ma=4附近。巡航段结束后,导弹质量变为450 kg。 30~45 s,导弹转入巡航阶段,其初始弹道如图3所示。由于设计的爬升弹道合理,导弹爬升结束时的高度与20 km只差16 m,据此高度误差产生的过载信号最大为1.8。45~500 s时巡航段为直线弹道,图4给出了巡航过程中的直线弹道。 图2 爬升段弹道 图3 巡航段初始弹道 图4 巡航弹道 ③下滑段。 500~560 s,导弹抵达战区并进入下滑阶段,高度由20 km降低到10 km,弹道仿真结果如图5所示,导弹最大飞行过载为3.2。制导参数K=-0.091。在工程设计中,如果导弹的最终速度大于或者小于盘旋速度,需要根据具体情况使导弹在下滑结束后继续无动力减速或较大推力加速。 图5 下滑段弹道 ④盘旋段。 560~620 s,导弹进入盘旋准备及盘旋阶段。此阶段导弹的初始质量为450 kg,发动机燃料消耗为0.83 kg/s,导弹的速度维持在Ma=0.7附近。结束盘旋后,导弹的最终质量为400 kg。由于指数弹道的特点,单纯采用高度变化律产生的导弹过载指令,很难直接将下滑段的最后高度变化为指令高度。为了保证导弹由下滑向盘旋转换的平稳性,在下滑末端弹道高度曲率变化不大的时候引入高度控制,导弹下滑段末端高度为10.043 km,与盘旋设定高度10 km相差不大,此时引入等高飞行控制,可保证导弹弹道平稳过度。 560~575 s,导弹进入初始平飞过渡段,如图6所示。 图6 初始平飞弹道 在575 s,导弹进入盘旋飞行,此时对偏航通道输入过载为5,导弹的盘旋直径为1.786 km。 575~620 s,导弹进入盘旋飞行弹道,如图7所示。 图7 盘旋弹道 ⑤俯冲攻击段。 在导弹的盘旋阶段已经启动了寻的导引,一旦发现地面目标或者接到指挥中心的指令,导弹将会立即俯冲进行打击。为了降低阻力,在5 s内导弹后掠角由最小35°变化为50°。经过53 s,导弹攻击到地面目标,终端与目标距离误差近似为6 m。 将变后掠翼巡航导弹的多任务飞行过程分为爬升、巡航、下滑、盘旋和攻击等5个主要阶段。本文采用指数形式的纵向程序飞行高度指令,保证导弹爬升和下滑段飞行的快速性和平稳性,使导弹顺利转入巡航和盘旋阶段;盘旋段采用覆盖作战区域的圆形弹道,根据导弹飞行速度和需要覆盖的战场区域面积获取制导指令;巡航段采用等高飞行直线弹道,采用经典超前校正环节的弹道高度跟踪控制器,实现等高飞行的弹道跟踪;攻击段采用比例导引律的自动寻的制导方案。弹道仿真结果表明,所设计的多任务弹道及制导指令合理,弹道转换平稳,满足远程变后掠翼巡航导弹多任务飞行和高精度制导要求。2.2 圆形盘旋弹道偏航程序过载
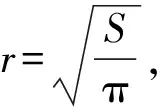
2.3 平飞段和攻击段的弹道及控制指令
3 弹道仿真
4 结论
