鲁棒控制在某型无人机航迹跟踪中的应用

张文广,易文俊,管 军,袁丹丹,张浩然

(南京理工大学 瞬态物理国家重点实验室,江苏 南京 210094)

随着无人机在直接作战中的应用,对无人机精确航迹与姿态的控制要求越来越高。由于无人机空气动力学特性复杂,受空气扰动、测量因素的影响,难以建立精确的数学模型[1]。当无人机的运动学模型不够精确时,对其进行控制时可能难以取得满意的效果,控制中会有较大的稳态误差,甚至可能出现发散的误差。国内外学者对这一问题提出了很多解决办法。如滑模控制[2-5]被广泛应用于无人机姿态控制,但是由于建模误差等原因,这种方法存在抖振的现象。一些新发展起来的方法,如微分几何方法也被应用于解决飞行器的控制问题[6-7],但此方法对模型的扰动也不具有鲁棒性。此外,还有参数自校正的方法[8-10],取得了良好的控制效果,但是当系统的多个参数存在扰动的情况下,该方法无法准确估计出参数真值,而是整体达到一种使系统误差降低的组合。

单纯的滑模控制或微分几何的方法无法解决系统参数摄动的问题,而自适应的方法又需要计算参数的更新率,这无疑增加了控制计算机的计算负担。本文考虑到实际中无人机的参数摄动是存在且已知的,在此基础上设计了一种简便的控制算法。本文的思想可以描述为:针对某固定翼小型无人机,构造含参数摄动上限的速度和姿态控制器,使系统在李雅普诺夫意义下是稳定的,且对于参数摄动具有鲁棒性。最后,将本文所提算法应用于该型无人机的航迹跟踪任务中,以验证其有效性。

1 模型的建立

1.1 定义与说明

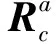
(1)

1.2 质心运动学建模

定义质心运动为[11]

(2)

(3)

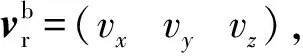
(4)

其中,攻角α定义为

(5)

侧滑角定义为

(6)

其中,合速度vT定义为

(7)

相对速度在速度坐标系下可以表示为

(8)

假设风速为常数,或者变化缓慢,则可用牛顿第二定律求得机体的加速度:

(9)

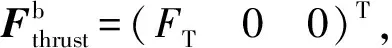
(10)

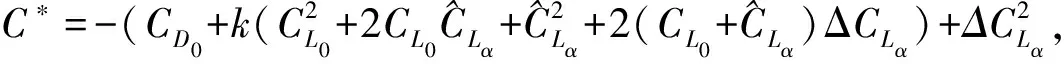
(11)

(12)

(13)

(14)

合速度对时间t的导数可以表示为

(15)

将式(9)代入式(15)中,得:

(16)

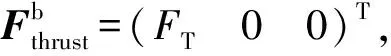
(17)

注意vT和vx为正值。

1.3 绕质心转动运动建模

固定翼无人机绕质心转动的运动可以建模为[12]

(18)

式中:

(19)

为惯性矩阵,J(·)是正的常数;u=(δaδeδr)T,为控制输入矢量,由3个偏向角组成;气动力矩函数定义为

(20)

定义:

(21)

(22)

(23)

(24)

(25)

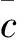
(26)

则有

(27)

上述式中各符号含义见文献[12]。

2 速度控制器设计

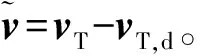
(28)

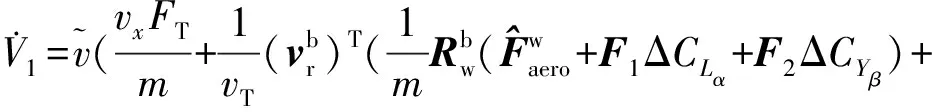
(29)

令

(30)

式中:KV为正的增益系数;ΔC(·)(·)Z=|max(ΔC)|,即摄动上限的绝对值;符号“∘”表示hadamard乘号,即矢量对应元素相乘。将制导律代入式(38),得:

(31)

3 姿态控制器

采用滑模变结构的方法设计姿态控制器[13]。

定义滑模变量为[14]

(32)

(33)

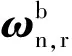
(34)

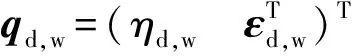
(35)

式中:I为单位矢量。

用惯性矩阵J左乘σb并对其求导,代入式(26),得:

(36)

式中参考角加速度变为

(37)

令Lyapunov候选函数为

(38)

(39)

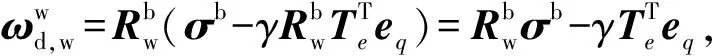
(40)

设计控制律为

(41)

式中:Ks是一个正定阵。

将控制律代入式(9),得:

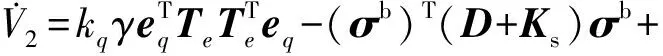
(42)

假设1:

sign(ηd,w(t))=sign(ηd,w(t0))∀t

(43)

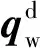
引理1[15]在假设1的条件下,可以得到如下不等式:

(44)

(45)

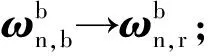
4 仿真结果

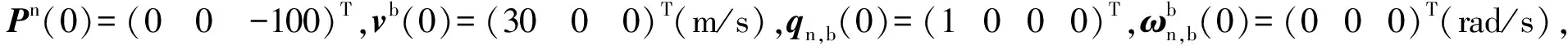
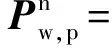
设置组合气动参数误差见表1。

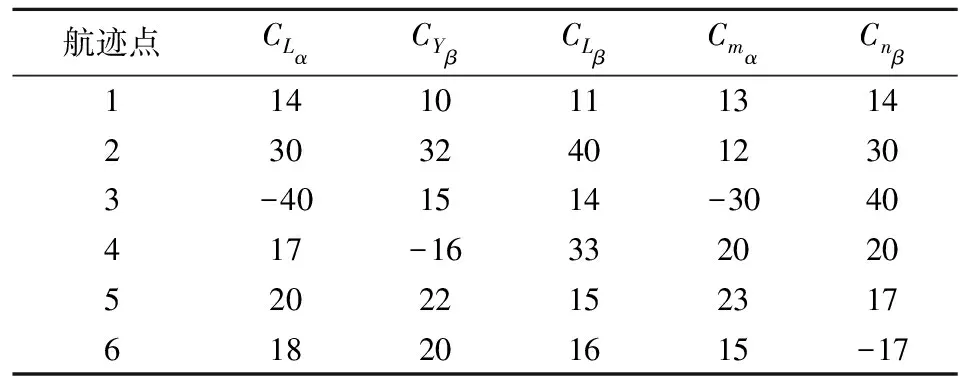
表1 各航迹点处设置的气动参数摄动 %

为进一步分析和验证本文所提算法的性能,将该算法与一种基于参数自适应校正的算法[8]进行对比。根据该自适应算法,重新设计V1:

(46)

(47)

令

(48)

(49)

同理,重新设计V2,得:

(50)

将V2对t求导,得:

(51)

令

(52)

(53)

(54)

上述式中参数A1,A2,N1,N2,N3为正的常数,本文中设置为A1=5,A2=6,N1=10,N2=8,N3=5,仿真的初始条件同前文。

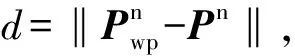
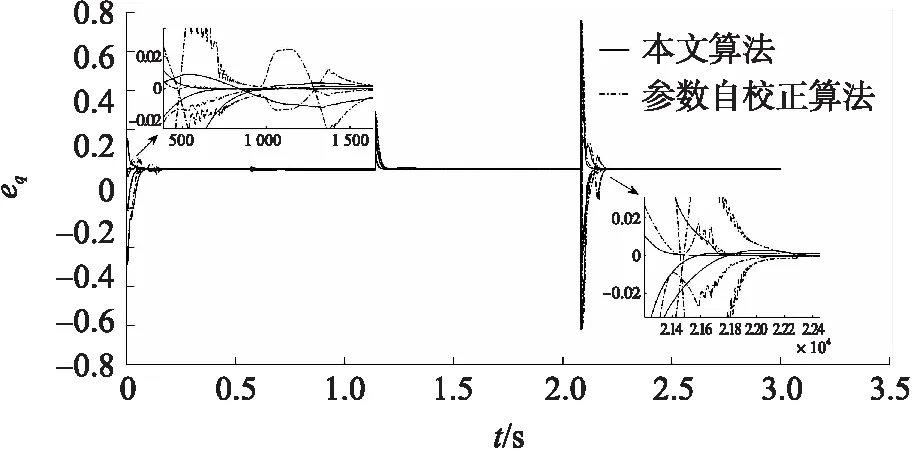
图1 姿态四元数误差

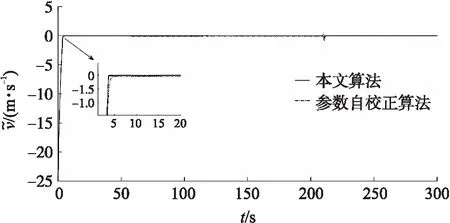
图2 速度误差对比

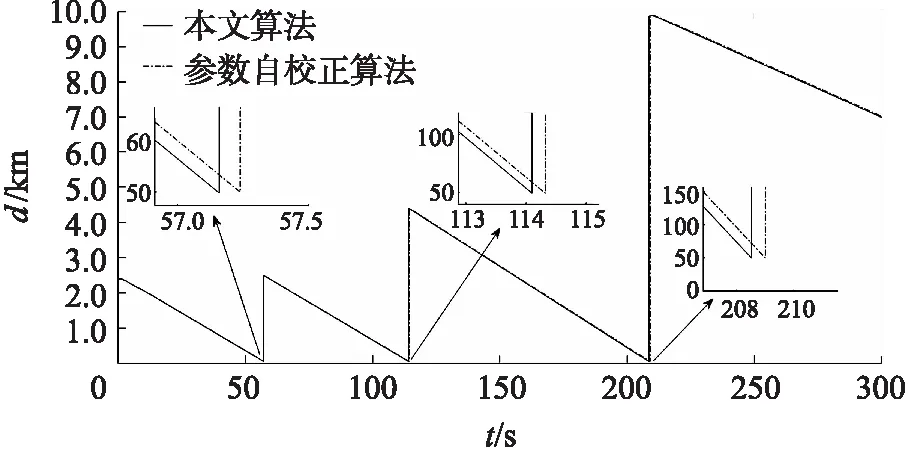
图3 跟踪距离误差

5 结束语

本文针对气动参数摄动设计了一种简便的控制算法,解决了无人机航迹跟踪控制中的实际问题,具有较大的应用价值。根据稳定性理论,设计含有参数摄动上限项并加入到控制输入中,从而抑制参数摄动对系统的不利影响。仿真结果表明,本文的改进算法可以保证较高的控制精度。