基于单目摄像头的3D动态手势交互*

王岩全，孙博文

(哈尔滨理工大学计算机科学与技术学院,黑龙江 哈尔滨 150080)

1 引言

在虚拟现实不断发展的今天，手势交互成为继鼠标、键盘、触摸屏之后新的人机交互方式。目前手势交互产品以Leap Motion、Kinect为主，尤其是Leap Motion的出现，使得一些需要借助于外部硬件设备(如数字手套)的手势交互方式黯然失色。但是，无论是Leap Motion还是Kinect都没有像鼠标、键盘一样普及，除了一些外部的环境因素，其自身的局限性是最大的原因。Leap Motion和Kinect主要针对游戏开发者与其公司发布的游戏交互产品，不适用于普通软件，而且比起鼠标、键盘等硬件交互设备，其价格十分昂贵。传统的单目摄像头已经做到以图像处理的方式在复杂环境中识别手势[1]，但无法对手势进行深度识别，而且其研究成果停留在了二维空间，没有做到像Leap Motion一样实时地识别动作(如抓取物体)。由此，以普通单目摄像头实现手势交互具有十分重要的意义。

基于神经网络的手势识别也是一种常用的手势识别方法[2]。由于手势具有尺度变换、旋转、平移等复杂变化，所以每种手势需要选取不同背景、不同旋转角度的有效图片各100张用于训练，因此基于神经网络的手势识别本质是对相同手势姿态的归类，并不是对手势姿态变化参数的提取。由于在神经网络层数较深的情况下计算量较大，无法保证交互的实时性，基于神经网络的手势识别适合运用于识别，并不适合于交互。

Leap Motion装有双红外摄像头，利用视觉差技术获取手关节的空间位置并实时追踪[3,4]，而Kinect装有RGB与CMOS红外摄像头、红外发射器，二者都是基于双目摄像头的手势交互。相比于此，单目摄像头实现空间交互有两大难点，手势的深度识别与手势的动作识别[5,6]。本文采用不同深度下手面积的变化确定深度值，以自创的匹配算法计算不同手势图像的匹配率，将不同手势动作的运动信息预存到程序中，以匹配率的高低选择不同的运动信息，达到动态手势交互的效果。

2 3D手势交互

2.1 匹配算法的选择

本文的技术核心是以最优的匹配率选择相对应的运动信息，匹配算法的选择不仅决定了原始图像的预处理方式，而且匹配率的高低直接影响手势运动信息的选择，决定着手势交互的正确性。特征匹配是通过提取图像的特征点来进行匹配的一种匹配方式[7,8]。如下实验证明基于特征点匹配方式并不适用于手势匹配。

实验以预制在3D场景中的手模型与摄像头信息进行实时匹配，实验效果图1和图2所示。

Figure 1 Matching effect when the hand is open图1 手展开时匹配效果

Figure 2 Matching effect when the hand is clenched图2 手握拳时匹配效果

如图1和图2所示，左边图像为摄像头拍摄的实时图像，而右边为3D场景中预制的手模型，匹配结果杂乱无章且严重受到外部环境的影响，不仅匹配错误频发，无法获取手的空间信息，手势的变化更是无法识别。因此，必须对图像进行预处理并提出自己的匹配算法。

2.2 颜色空间转换

一般图像都是基于RGB颜色空间的[9]，而人体肤色容易受到光照等亮度因素的影响，为了剔除亮度的影响，将RGB空间转换为YCrCb空间。通过剔除表示明亮度的Y通道，保留表示色度的Cr与Cb通道，就可以忽略亮度的影响，将三维RGB空间降到二维CrCb空间[10]，如图3～图5所示。转换公式如下：

Y=0.257×R+0.564×G+0.098×B+16,

Cr=0.439×R-0.368×G-0.071×B+128,

Cb=-0.148×R-0.291×G+0.439×B+128

(1)

Figure 3 Result of Y color space图3 Y颜色空间图

Figure 4 Result of Cr color space图4 Cr颜色空间图

Figure 5 Result of Cb color space图5 Cb颜色空间图

2.3 图像二值化

剔除Y通道，保留CrCb通道后，以Cr值在133～173、Cb值在77～127为依据，判定该点为肤色点，其他部分就为非肤色点。将0～255亮度等级的灰度图像进行阈值选取，对灰度图像进行阈值选取，将图像转化为二值图[11,12]。转换公式如下：

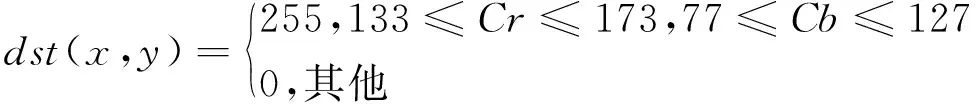
(2)

如图6所示，图像中肤色与肤色相近的成分转换为白色，其余部分转换为黑色。为了剔除非手势部分，下面计算图像轮廓面积。

Figure 6 Result of binary process图6 二值化图

2.4 计算图像轮廓面积

在二值化后的单通道图像中，像素值分为0与255。可以根据相邻像素点像素值大小的变化绘制轮廓图[13,14]。轮廓由像素点集合构成，在程序中以序列的方式存储于内存中。

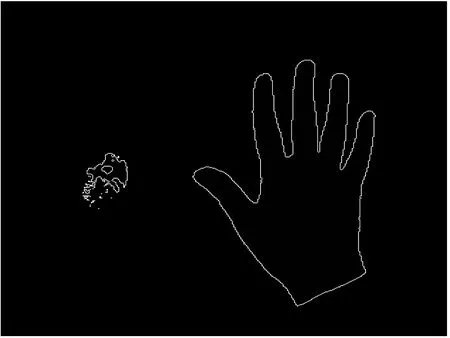
Figure 7 Contour of gesture图7 手势轮廓图

图7所示为白色轮廓的手势轮廓图。由于不规则轮廓的面积难以计算，且此处仅仅是利用面积的大小进行比较来剔除其他的轮廓，因此采用轮廓所围像素点的个数来近似取代轮廓面积进行比较。根据轮廓像素点集合的位置信息，对像素在相同y轴下x轴的坐标由小到大，方向由y轴方向从小到大进行计数，统计像素值为255的像素点个数。

(3)

不同手势面积的大小范围可以根据实验获得。在此处手势交互中，手的轮廓面积比其他非手轮廓面积大，因此只需要设置最小值来剔除其他轮廓。

图8为剔除非手势区域后的图像。在剔除非手势区域之后就可以对手势区域进行截取。

Figure 8 Binary image after eliminating other contours图8 剔除其他轮廓后的二值图

2.5 手势提取

剔除非手势因素之后，为了更容易地进行图像匹配，需要截取图像中的手势。通过比较轮廓像素点中的x轴坐标值与y轴坐标值的大小，选出最大与最小x轴坐标值y轴坐标值的四个像素点，以四个像素点位置为基准截取手势。截取到的手势区域如图9所示。

Figure 9 Gesture图9 手势图

由于截取的图像大部分为长方形，不便于之后的图像匹配，需将图像转换为正方形。如果将长方形图像直接进行尺寸缩放，手势轮廓必然会发生变形，此处选取长和宽中较长的边为基准重新进行截取，此时截取的图像为正方形，再次进行尺寸缩放时手势不会发生变形。调整后的手势图如图10所示。

Figure 10 Adjusted gesture图10 调整后的手势图

2.6 图像匹配

为了更好地实现手势的匹配，本文的匹配算法不仅需要区分不同的手势，而且还要计算出明确的匹配率。

为了方便匹配，将所有手势进行尺寸缩放，这里将其缩放为100×100像素大小。采用线性插值算法对图像进行缩放,如图11所示。缩放图像的像素值根据映射到源图像附近的四个邻近像素的线性加权计算得出，权重与四个像素点的距离成反比。这里以sx，sy表示源图像像素点的横坐标值和纵坐标值；sw，sh表示源图像的宽度与高度；dx，dy表示目标图像像素点的横坐标值和纵坐标值；dw，dh表示目标图像的宽度与高度；a1，a2,a3，a4表示源图像中与目标图像相对应像素点的邻近的四个像素点的像素值；k1，k2，k3，k4表示四个点的权重；x表示目标图像的像素值。

Figure 11 Schematic of linear interpolation algorithm图11 线性插值原理图

x由a1，a2，a3，a4四个值加权平均求出。通过计算目标像素点在整个图像中的相对位置可以计算出与其相对应的源图像中像素点的坐标值。计算出的坐标值为小数，通过坐标值的上取整和下取整与坐标值之间的差值可以计算出各个权值。计算公式如下：

x=((a1×k1+a2×k2)+(a3×k1+a4×k2)+(a1×k3+a3×k4)+(a2×k3+a4×k4))/4

(4)

sx/sw=dx/dw，则sx=dx×sw/dw,

sy/sh=dy/dh，则sy=dy×sh/dh,

缩放后的手势图如图12所示。

Figure 12 Scaled gesture图12 缩放后的手势图

由此便可计算出目标图像每个像素点的像素值。在完成图像缩放之后，接下来就是对图像进行匹配。在进行手势交互时，应该预先将不同的手势图像预制到计算机中，这样就可以实时将摄像头读取的图像与预制的图像进行匹配。这里将目标图像的每个像素点与预制图像每个像素点的像素值大小一一比较，统计出相同位置像素值相同的像素点个数count，用count除以总像素点数也就是10 000,便可求出不同目标图像与预制图像的匹配率rate。由于图像在缩放时进行了插值算法运算，轮廓边缘点的像素值不一定会等于0或255，因此在对count进行计数时，目标图像与预制图像在相同位置像素点的像素值如果不同时等于0或255时也进行计数。这里将这种匹配算法称为完全重叠匹配。完全重叠匹配算法不仅可以计算出不同手势(如握拳与展开)的匹配率，而且细微手势动作变化(如绕空间某个方向旋转1度)的匹配率也会产生变化。这样就可以根据目标图像与不同预制图像匹配率的高低选择最合适的运动信息。

计算匹配率，首先计算count，当两幅图像所有相同位置的像素值同时为0,或者同时为255或者既不是0也不是255时，对count进行计数，将计数完后的count除以图像像素点的总个数得到匹配率。计算公式如下：

count=

rate=count/10000

(5)

Figure 13 Matching rate of different gestures图13 不同手势的匹配率

如图13所示，不同手势图与预制手势图的匹配率各不相同。理论上，相同手势的匹配率应该为100%，但由于手在现实场景中的动作不可能与录入时的动作完全一致，且摄像头的摆放位置、角度也不一定完全相同，但是相较于其他不同的手势，相同手势间的匹配率最高，且与不同手势间的匹配率相差较大，足以用来区分其他手势，从而选择正确的运动信息。

2.7 提取目标图像的空间运动信息

目标图像是由摄像头获取现实场景的手势信息再加上前期的图像处理实时生成的，在手势发生变化时，目标图像也在实时地变化。手在二值图中的坐标也在同步变化，通过实时比较当前手势位置与前一时刻手势位置的变化便可以获取手势在平面上移动的方向。如图14所示，这里选取e点作为手势坐标的基准点。在手势位置没有发生变化，但动作发生变化时(如握拳)，图中五点a、b、c、d、e除了e点之外，其余四个点的坐标都会发生变化。因此，选取e点作为手势位置基准点，这样就避免了手势位置没有发生变化而动作发生变化带来的对手势移动信息的误判。通过当前时刻的手势位置的坐标值减去上一时刻手势位置的坐标值的正负和大小来判断移动的方向与速率。

Δx=xt2-xt1,

Δy=yt2-yt1,

depth1=k×s1+g,

depth2=k×s2+g

(6)

其中，Δx与Δy表示e点在x轴方向与y轴方向的偏移量。xt1与xt2表示e点在t1时刻与t2时刻的横坐标，yt1与yt2表示e点在t1时刻与t2时刻的纵坐标。depth1与depth2为不同时刻的手势深度值，s1与s2为不同时刻的手势面积。通过联立方程组可以求出手势面积与手势深度之间的线性参数k与g。

Figure 14 Change of rectangular coordinate图14 矩形框坐标变化

接下是来获取深度信息。这里采用手势轮廓面积的大小来判断深度值。由于同一深度下不同手势面积不同，因此不同手势应运用不同的判断基准。通过选取不同手势在两种深度下的轮廓面积，联立方程组计算出不同手势深度与手势面积之间的线性参数k与g，就可以计算出不同手势的深度值。

2.8 3D模型的空间移动与旋转

在三维坐标系中，各种手势姿势都可以经由基本的手势经过平移与旋转得到，而平移与旋转属于图形几何变换中的两种基本变换，复杂的几何变换可以通过基本的几何变换复合实现。例如，手的3D模型的几何变换，可以将其中一点的复杂几何变换分解为基本的平移与旋转变换，再根据原模型的拓扑关系连接新的顶点实现整个模型的几何变换。而这些基本的变换是通过引入齐次坐标技术实现的。通过将三维空间中的复杂问题扩展到四维空间，可以将几何变换转换为矩阵相乘的数学表示，借助于计算机的高速处理，实现手模型的移动与旋转。

由于摄像头坐标系与3D场景坐标不同，手移动时要调整代表移动方向的数值正负。

由图15可知，摄像头坐标系的x轴与3D场景坐标系中的x轴同方向，所以现实中手势在x轴变化的方向与3D场景中手势模型的变化方向相同，摄像头坐标系的y轴方向与3D场景中的y轴坐标系方向相反，所以在进行矩阵变换时，y轴坐标值前要加负号。

模型在3D场景坐标系中的x轴与y轴方向的坐标值是通过初值加变化值确定的，而在z轴方向的坐标值是通过手势面积的线性运算直接得到的，不需要进行平移变换。

[xyz1]=

(7)

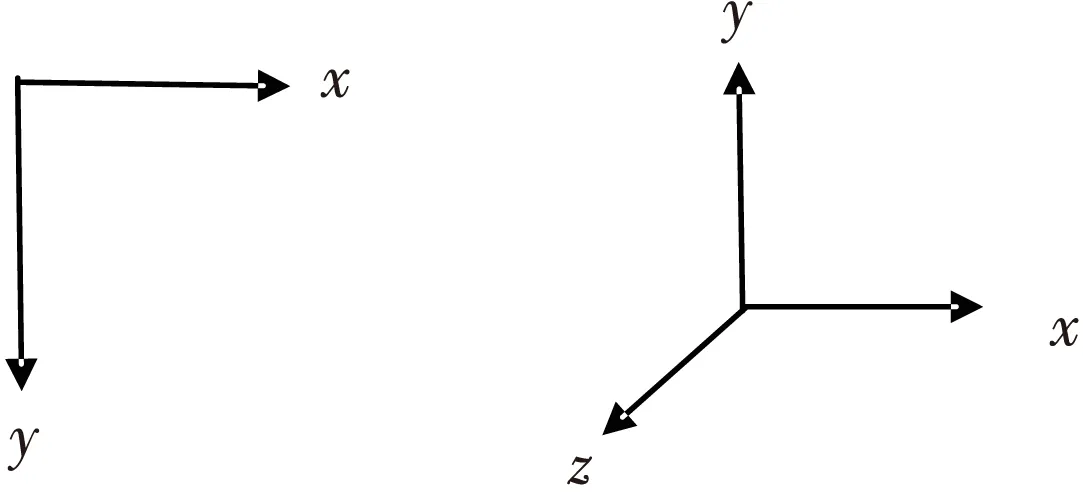
Figure 15 Coordinate system of camera and 3D scene图15 摄像头坐标系与3D场景坐标系

通过不断计算模型的空间坐标值就可以实现模型的空间移动。在完成模型的空间移动之后，接下来要实现手的动作变化。任何手动作变化都可以通过手指关节的旋转实现，而每个手指关节都是绕它的上一个关节进行旋转的。关节点的坐标值可以通过绕前一个关节轴的三维旋转变换得到。这里将绕关节点轴旋转的三维旋转问题转化成平移、旋转的复合变换，抽象为矩阵连乘的数学公式。定义要旋转关节点的坐标为(xa,ya,za)，关节点所要旋转的角度为θ，其所绕关节点的坐标为(xb,yb,zb)，所绕的轴为L、轴L经过关节点(xb,yb,zb)，且轴L绕3D场景坐标系中的x轴旋转α角，绕y轴旋转β角后会与z轴重合。α与β可以通过模型在3D场景中的欧拉角得出。

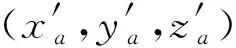
(8)

通过预先载入关节旋转角度，计算机不断计算关节点的位置就可以实现各种手势动作交互。

2.9 交互实时性

交互不仅要保证正确性，还要保证实时性。本实验交互实时性体现在3D场景的流畅程度，这里用帧数作为实时性的判断标准。交互达到24帧/秒便认为交互流畅，满足实时性要求。普通摄像头的帧数在30帧/秒左右，也就是说摄像头获取一张现实场景图像的时间在33.33 ms左右，将获取图像的时间加上图像预处理、图像匹配到最后得出手运动信息的时间看做一个周期。可以用程序测出整个周期中获取图像后处理图像的时间，大约为34 ms。也就是说交互处理一帧的时间为67.33 ms，换算成帧数约为13帧/秒。由此可以看出程序处理图像的时间过长，会导致交互不流畅。而程序处理图像的时间主要集中在图像匹配部分。由于完全重叠匹配需要比较大小为100×100图像的

每个像素点，每处理一帧图像程序都要循环10 000次，因此必须调整图像的大小以缩短图像处理时间。

由表1可知，随着图像尺寸的缩小，程序运行时间越来越快，帧数越来越高，但是匹配的正确率越来越低，这是由于图像在运用插值法缩放时，像素值为0与255的像素点个数越来越少，黑白成分越来越少，图像变得模糊，匹配率下降。当图像尺寸为30×30时，交互界面的帧数达到26帧/秒，匹配正确率为98%，完全可以满足实时性要求。

3 实验效果

为了展现交互的效果，这里预制手展开与抓取图像，并将手展开与抓取的运动信息预存到程序当中，从而实现手抓取物体的交互。抓取场景物体，将其放到木箱上。实验效果如图16所示。

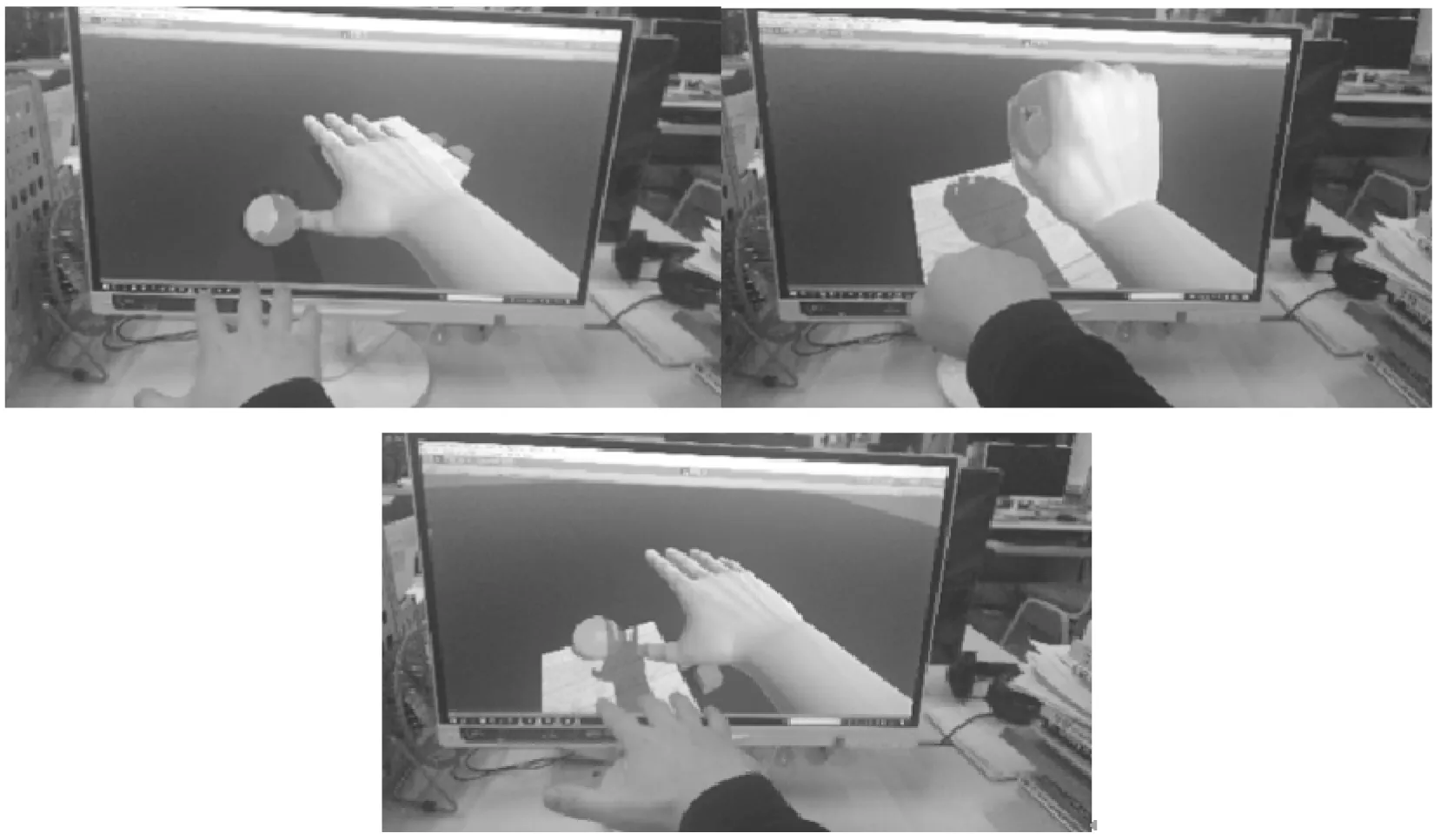
Figure 16 Gesture interaction of grasping objects图16 抓取手势交互

只要预制不同的手势图像与运动信息，就可以实现不同的手势交互。实验效果如图17所示。

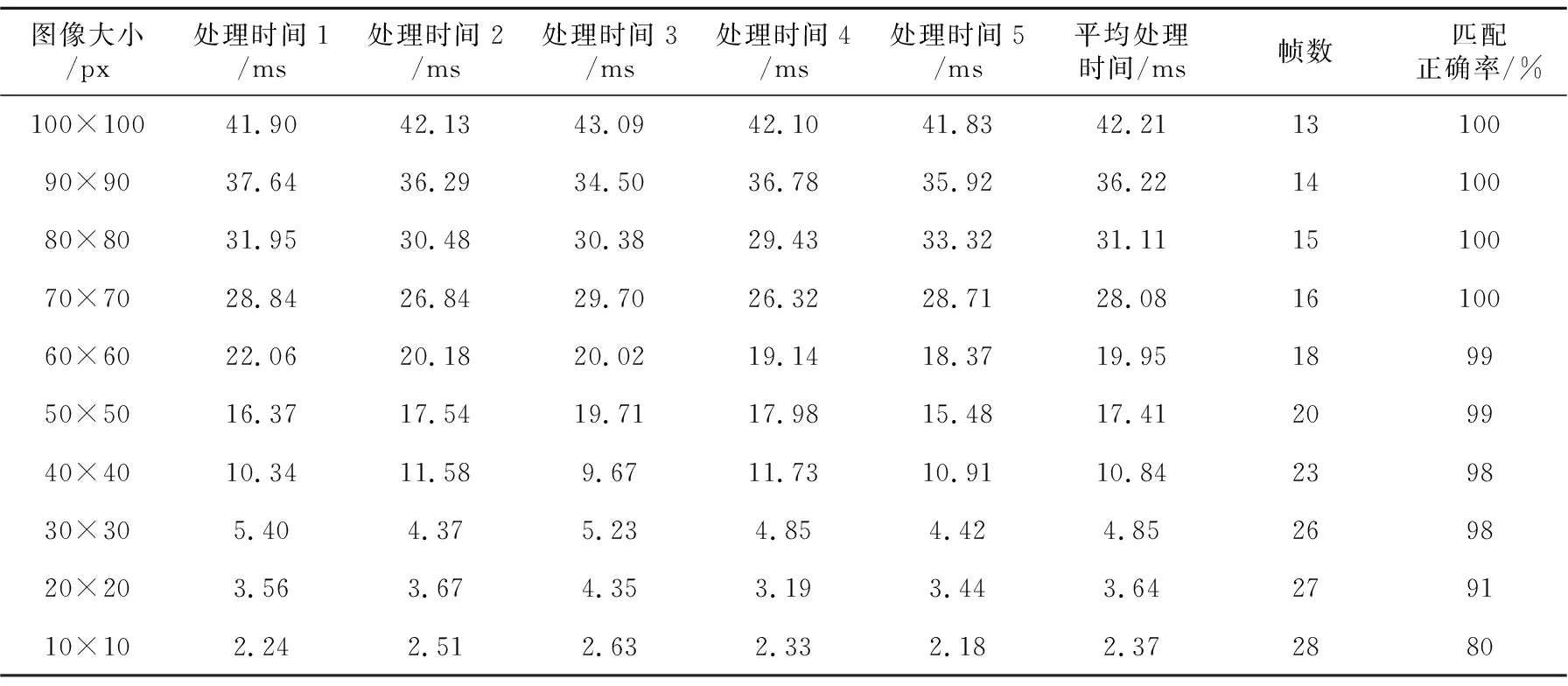
Table 1 Real-time comparison among images of different sizes表1 不同大小图像的实时性比较

Figure 17 Different hand gestures图17 不同的手势动作

4 结束语

在虚拟现实和增强现实不断发展的今天，人们在追求视觉真实感的同时，也在追求交互的真实感。尤其在游戏领域，传统的鼠标键盘逐渐无法满足人们的需求。现今的交互设备由于价格等因素，并没有普及到人们的日常生活中。本文基于普通的单目摄像头通过获取现实场景中手的图像并对其进行图像处理，获取其移动信息，再结合图像匹配的方式选取不同手势的动作信息来完成手势交互。不仅保证了交互的正确性，而且通过实验选取合适的图像尺寸，保证了交互的实时性。交互不需要借助专用的手势交互产品，使得手势交互更加便捷与普及。