基于模糊优化的关键词广告预算分配策略*

王中兴,黄美婷，覃朝勇

(广西大学数学与信息科学学院，广西 南宁 530004)

1 引言

随着电子商务的迅猛发展，互联网广告成为了一种强有力且备受青睐的网络营销手段[1]。其中，关键词广告是一种付费的文字链接型互联网广告，因为其具备了目标明确且针对性较强、成本低且预算可控、操作容易且广告效果明显等优点[2]，成为了时下备受广告主欢迎的在线营销和塑造自己品牌形象的重要营销方式。同时，这些现象在国内外学术界也掀起了关注的热潮，目前关键词广告已成为管理学、营销学、电子商务、计算机科学等领域的研究热点[3]。

关键词广告是一个动态的、连续的、多阶段的竞价过程[4]。竞价前，广告主需先选定投放关键词广告的搜索引擎网站，其后结合网站的特点以及产品属性，选择多个有价值且潜在点击率高的关键词，对其设计相应的竞价广告内容，并设置每一个关键词在每个时段的预算，估算每个关键词不低于最低拍卖价格的竞标价格。竞价时，当网站的用户在搜索引擎上搜索相关的关键词时，搜索引擎方的后台会按照关键词广告竞价排序规则将该关键词相关广告的链接呈现在搜索引擎的结果页面上。当网站用户点击关键词的广告链接后将会转入广告主的广告网页，此时广告主需按照关键词广告的支付规则向搜索引擎方支付此次的点击价格。

就目前而言，学术界中针对关键词广告的相关研究主要包括三个方面：关键词广告竞价机制的研究[5,6]、现有关键词广告拍卖机制的均衡分析[7,8]和关键词广告竞价策略的研究[9,10]。随着对关键词广告相关研究的深入，关键词广告的预算分配策略成为了近年来最受学者们关注的研究热点之一。广告的预算分配是制定关键词广告竞价策略务必解决的首要问题，合理的预算分配使得关键词广告“自上而下”地优化推广，进而使得广告主在激烈的竞争中占得先机[11]。

Feldman等[6]针对广告主在单一搜索引擎上竞标关键词广告的基于NP难问题提出了关键词广告的两标价策略。Zhou等[12]将预算约束下的关键词广告最优竞价问题视为在线背包问题，分别提出了单个广告位和多个广告位的最优竞争比算法，但是应用该算法的前提条件是已知每个广告位的点击率以及竞争对手的竞标价格，因此该算法在实际应用中较难实现。Sethi[13]研究了预算约束下的广告最优控制问题，提出了关键词广告Nerlove-Arrow动态竞价模型，并验证了广告总预算决定着预算的分配决策。Cholette等[14]针对单个搜索引擎，提出了投放关键词广告时的关键词选择最优规则、广告最佳竞标策略，建立了广告预算限制下关键词广告的最优线性规划模型。Shin[15]研究了多个广告主竞拍关键词广告时，在预算约束下的广义第二价格关键词拍卖机制，扩展了关键词广告的动态竞价模型，他认为在这种机制下，无论有无预算约束，广告主的竞价值都会高于自身的价值。Fruchter等[16]基于最优控制理论，构建了广告预算在两种不同门户网站间进行分配的模型，分析了广告预算分配、广告点击率以及用户基数三者之间的非线性关系。

陈李钢[17]针对单搜索引擎和多个搜索引擎，提出了最优关键词广告竞价预算分配策略，建立了最优广告控制模型。同时，Chen等[18]还针对跨门户网站，提出了竞价时广告的非线性最优预算分配决策模型。侯乃聪等[19]研究了预算限制下多个关键词的竞价排序投资策略，构建了多个关键词同时被检索时的基本模型以及转化模型，得到了关键词的数量较少或较多时的竞价排序方法。杨彦武等[11]从跨搜索引擎以及时序两个方面研究了关键词广告竞价时的预算分配问题，提出了点击量是衡量广告主广告利润的标准之一，而使得广告主利润实现最大化的有效途径是最小化损失掉的点击量，构建了以最小化损失掉的点击量为目标的关键词广告两阶段模糊预算分配模型，得到了广告预算分配后如何调整的优化策略。事实上，除广告的点击量之外，广告转化率也是影响广告收益的因素之一。韩帅等[20]研究了基于VCG(Vickrey-Clark-Groves)拍卖机制的预算约束下的关键词广告拍卖策略，提出预算约束的全局无嫉妒均衡条件，并分析了均衡时的预算阈值。刁秀杰等[21]基于最优控制理论，提出选择所分配预算占总预算的百分比作为控制变量，建立了跨搜索引擎关键词广告在三种不同的拍卖机制下预算分配模型。

由上述内容可知，目前国内外的关键词广告预算相关研究主要可分为两方面：一是以预算为约束条件对广告关键词的选择以及竞标策略等展开的研究，这一方面的研究中，广告预算不是研究的主要对象，而是作为一个约束条件以探究关键词广告的竞价投标策略；二是研究广告主在单一或多个搜索引擎投放关键词广告时的广告预算分配策略，这一方面的研究以预算为主要研究对象，集中探讨如何分配预算使得广告主获得最大利润，其中以从多个搜索引擎角度建立单目标预算分配模型的研究居多。由此可见，单一引擎上的关键词广告预算分配策略的研究仍为鲜少，这方面的研究依然缺乏能够进一步推广的成熟的理论体系。

本文将研究广告主在单一搜索引擎上竞投关键词广告时，如何合理地对多个关键词的预算进行分配以使得广告主获得最大收益的策略，构建以广告收益最大化、无效点击量最小化为目标函数的单搜索引擎多关键词的竞价广告时序预算双目标优化分配模型，并基于多目标模糊优化理论以及线性规划方法的知识，提出了求该双目标优化分配模型的有效解法。

2 单搜索引擎多关键词广告预算分配模型

假设某广告主在某单一搜索引擎上针对自家产品竞投关键词广告。在关键词广告拍卖的前期，广告主必须在海量的关键词中选出多个对产品有着代表性且能够突显广告价值、存在一定的潜在点击量、能够提升广告转化率的关键词。每一个关键词的竞标价格决定着广告在搜索引擎页面的位置，广告排位是广告点击量的重要影响因素之一。一般地，广告排位越高，被搜索引擎用户点击的机率就越大。本文假设广告主的竞标价格和投资的总预算等投标条件足以保证广告主能够拍卖到某一广告位，而关于如何选择关键词，在此文中将不展开研究。

在关键词广告竞价的过程中，广告的收益对广告点击量存在着很强的依赖性，广告的点击量越高，广告主获得的广告收益也就越高，同时随之增加的还有广告成本。尽管广告收益随着广告点击量的增加而增加，但广告收益的增加并非与广告点击量的增加成正比例，因此不能以广告的点击量作为衡量广告收益的唯一标准。除了广告的点击量之外，广告的转化率即用户产生了转化行为的点击量占广告总点击量的比例也是广告收益的重要影响因素之一。我们可以通过减少不发生转化行为的广告点击量来实现广告转化率的提高，从而提高广告的收益。假若将不产生转化行为的点击视为无效点击，则无效点击越少广告的转化率越高，广告主想要获得最大利润，必须在获得最大广告点击量的同时最小化总广告点击量中的无效点击。在总预算限制下，不同时段不同关键词的预算分配非常重要，合理的预算分配能在节省广告成本的同时提高预算的有效使用。广告主在进行关键词广告竞标时必须针对竞标的目的，分析搜索引擎市场的现状和近期的广告市场动态来预估关键词广告竞标的预算在不同时段不同关键词上的分配，以确保达到最优的竞标效果。

2.1 模型建立

在总预算限制的情况下构建广告预算分配双目标优化模型，如下：

(1)

(2)

(3)

xkt≥0,k=1,2,…,K;t=1,2,…,T

(4)

其中，R为总的收益，C为总无效点击量。

2.2 目标函数模糊化及模型求解

求解多目标优化模型，实际上就是在寻找一个使得每个单目标都能趋近于最优的折衷解的集合的过程。在上述的多目标优化问题中，每个关键词在每时段的最优预算都具有不确定性，即约束条件和目标函数是存在着模糊性的。因此，基于多目标模糊优化理论，可将多目标问题转化成单目标问题进行求解。但是，在求解多目标模糊优化问题之前，我们必须先确定每个目标函数的隶属函数。模糊数学中，目标的隶属函数代表着目标函数能实现的最优程度，即隶属函数越接近于1，目标函数就越接近于最优解。

上述多目标优化模型中，因为公式(1)为最大化广告主的广告竞价利润，即利润越大越好，所以选取了偏大型的升半梯形分布函数为其隶属函数。公式(2)考虑降低无效点击概率，最小化无效点击量，即无效点击量越小越好，因此选用了偏小型的降半梯形分布函数作为该目标函数的隶属函数。两个目标函数的隶属函数分别用公式(5)和公式(6)表示。

(5)

(6)

其中，μR和μC分别为公式(1)和公式(2)的评价属性隶属度；Rmax和Rmin分别为公式(1)在约束条件下，广告主所获得的广告收益的最大值和最小值。同样地，Cmax和Cmin分别为公式(2)在约束条件下，所产生的无效点击量的最大值和最小值。

根据多目标模糊优化的理论知识，将单引擎平台多关键词广告预算分配双目标优化模型转化成单目标优化问题，即求解满足两个目标及所有约束条件的隶属度λ最大化问题，于是得到单引擎平台多关键词竞价广告预算分配的模糊优化模型如下所示：

maxλ

s.t.λ≤μR

λ≤μC

xkt≥0,k=1,2,…,K;t=1,2,…,T

0≤λ≤1

(7)

将公式(5)和公式(6)分别代入公式(7)中，再结合公式(1)和公式(2)，公式(7)可转化为求解如下单目标规划问题，利用现有的线性规划方法即可求出最大满意度以及分配策略。

maxλ

s.t.λ(Rmax-Rmin)+Rmin≤

xkt≥0,k=1,2,…,K;t=1,2,…,T

0≤λ≤1

(8)

3 算例

本文以某广告主在单一搜索引擎上竞标5个关键词的广告为例，其竞标周期为5天，投入的总预算为500元。具体的参考数据如表1所示。

若利用平均分配法分配总预算，则每天每个关键词的预算为20元，整个竞标阶段所产生的无效点击量共为3 432，总收益为1 528.6元。若依据本文构建的分配模型进行实验，结果如表2所示。

每时段的最优预算分配为：

(9)

Table 1 竞价数据表表1 Data of bidding

Table 2 仿真结果表2 Result of simulation

其他时段的预算分配为0。

实验的结果表明了若根据本文的模型进行预算分配，竞标关键词广告时广告主所获得的总收益为2 604.6元，产生的无效点击量为3 178。该模型的结果与平均分配预算法相比的结果，广告主的收益增加了约70%，同时广告的无效点击量减少了约7.4%。由此可知利用本文所建立的关键词广告预算分配优化模型能够有效地减少广告的无效点击，从而减少无效点击产生的广告成本，提高广告预算的使用率和转化率，最终达到使广告主获得最大收益的目的。可见本文模型是可行的且有效的，对广告主在预算分配策略方面有着一定的指导性作用。

4 讨论与分析

本文的预算分配优化模型中，随着广告主投入的广告预算越大，所获得的广告点击量xktckt就越大。相应地，广告主的总收益R以及无效点击C都将随着点击量的增长而增加，但并非随之无限增加。当总收益R上升至某一数值时，由于受约束于公式(2)以及约束条件，使得其增长速度开始逐渐下降且趋向于零。最终当总收益R的增长速度降为零时,此时相应的xkt为最优解，总收益R达到了最大临界值。同样地，由于受约束于公式(1)以及其约束条件，在总收益R达到最大临界值时，无效点击C也达到自身的最小临界值。这两个临界值并非各自单目标函数优化时的最优值，却是两个目标函数同时进行优化时的最优值，因此该xkt为双目标优化模型的最优解。

如图1和图2所示，分别为广告主在总预算限制为500元的情况下，竞标周期为五天以及关键词为五个的预算分配情况。

Figure 1 Daily budget allocations图1 每天的预算分配情况

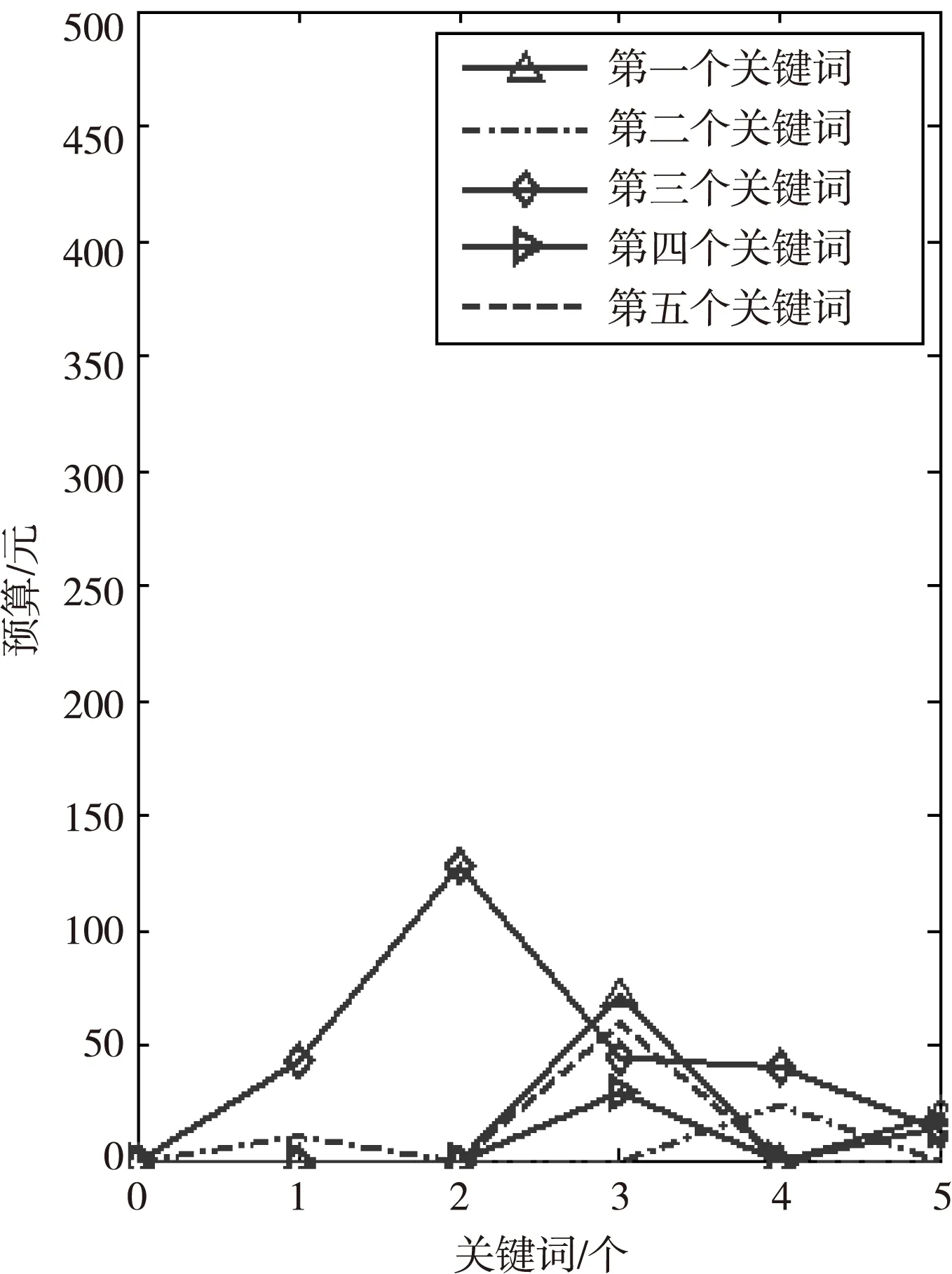
Figure 2 Budget allocation for each keyword on a daily basis图2 每个关键词每天的预算分配情况

图1是每天的关键词的预算分配情况。由图1可知，五天的预算分配占总预算的百分比分别为：10.7%、25.7%、41.2%、12.9%以及9.5%,很明显广告主将大部分的预算分配到了第二天和第三天，其中第三天的预算分配最多。

图2为每个关键词每天的预算分配情况。五个关键词的预算分配占总预算的百分比分别为：18.31%、7%、53.69%、9%以及12%。广告主在第三个关键词投入的预算远远多于其他四个。由图2可知，广告主将25.69%的预算分配到了第二天第三个关键词的广告中。第三天广告主同时对四个关键词进行广告投放，是五天中竞价关键词个数最多的一天。

在广告预算不断变化寻找最优解的过程中，总收益R和无效点击量C相应地发生变化，如图3和图4所示。

Figure 3 Change of total revenue图3 总收益变化情况

Figure 4 Change of invalid clicks图4 无效点击变化情况

图3中，随着总预算的不断投入，广告的总收益不断增长；由于受到约束条件和最小化无效点击的限制，当总预算增至350元时，广告总收益的增长速度开始逐渐下降；当总预算达到固定值500元时，广告总收益增长速度为零，得到的最优值为2 604.6。

图4中，随着总预算的不断投入，无效点击量不断增长；同样地，在约束条件和最大化总收益的限制下，当总预算增至300元时，无效点击量的增长速度开始下降；当总预算达到固定值500元时，无效点击量增长速度为零，得到的最优值为3 178。

图5为广告总收益与无效点击量相互约束、相互影响的情况。广告总收益和无效点击量作为模型的两个相互制约的目标，在开始时，无效点击量随着广告收益的增长而增加，在满足预算约束限制条件时，广告总收益和无效点击量达到最优值。

Figure 5 Interaction between advertising revenue and invalid clicks图5 广告收益与无效点击量的相互影响

5 结束语

本文从广告主的角度，建立了单搜索引擎多个关键词广告时序预算双目标优化分配模型。模型中，目标函数为最大化广告收益及最小化无效点击量，并基于模糊优化方法，将双目标模糊优化的问题转化成了单目标优化的问题来求解最优值。该预算分配优化模型，能够在一定程度上提高关键词广告预算的使用率，克服了以往研究中片面追求广告效益的弊端，使得广告主在预算限制的情况下可以通过降低无效点击量的方法，从而减少竞价成本以获得更高利益。本文的模型是有效、合理的，目标函数意义清晰明确，为广告主在单引擎平台竞标多关键词广告时的预算分配策略提供了较为完善的多目标模糊优化模型与方法。