基于CLF的移动舞台机器人轨迹跟踪预测控制
2018-10-08,,,
,,,
(浙江工业大学 信息工程学院,浙江 杭州 310023)
随着我国人民的精神文化追求日益提高,舞台演出艺术成为日常文化生活中的重要组成部分,其中移动舞台机器人是呈现高品质舞台演出艺术的重要道具之一.通常在舞台演出时,移动舞台机器人需要根据演出要求,同时考虑演出人员和舞台安全,在预定的有限区域内快速且稳定的到达并最终以给定的速度跟踪运动平面上给定的某条轨迹.由于纯滚动无滑动这一非完整约束的存在,移动舞台机器人移动控制的本质是非完整移动机器人运动控制问题.为了解决该类问题,国内外学者进行了大量的研究[1-4],提出了各种各样的方法,主要包括传统控制理论方法和智能控制方法两大类.但这些方法普遍存在鲁棒性差、缺乏自适应性的缺陷.例如:沈敏等[5-6]使用了模糊控制方法,但是模糊控制需要专家经验建立模糊规则,如果不能建立理想的模糊规则,控制效果将受到直接影响.董辉等[7]提出了一种变增益反馈D型迭代学习控制算法,使机器人在强耦合非线性环境下能够快速并较好的完成轨迹跟踪任务.马海涛等[8-9]使用滑模控制的方法实现了轨迹跟踪,该方法的主要问题在于控制律中的不连续项会直接转移到输出项,使系统在不同的控制逻辑之间来回高速切换,引起系统出现不可避免的“抖振”现象[10],实际控制效果较差,这是滑模控制方法的特性本身决定的.Kanayama等[11-12]提出了利用 Lyapunov函数法设计全局轨迹跟踪控制律的方法,虽能够达到轨迹跟踪的目的,但忽略了控制律中可调参数的影响.Krzysztof等[13]利用 Backsteping的思想设计了轨迹跟踪控制律,不但控制器的结构设计十分复杂,并且控制律中同样含有可调参数.研究中发现,控制器参数设置是否恰当,直接影响到跟踪效果.
模型预测控制(MPC)由于采用滚动优化控制原理,可以在一个最优控制的框架内灵活而显式地处理系统的各种约束、非线性因素和性能指标等实际要求[14-16],对于解决移动机器人的跟踪控制问题具有独特的优势.由于MPC的计算量通常随决策变量维数呈指数增长,因此可以通过降低在线计算维数的方法来提高MPC优化的计算效率.受参数化[17]设计思想启发,提出了一种参数化MPC算法求解移动舞台机器人速度和状态受约束的轨迹跟踪问题.其基本思想是针对移动舞台机器人的误差系统模型,构造它的一个控制Lyapunov函数(CLF),利用CLF法设计可调预测控制器,并通过在线滚动优化给定性能指标计算控制器的可调参数,实现预测控制量的在线确定,在保证控制器具有一定自适应性的同时降低了计算量.最后,以圆为参考轨迹做了仿真验证,仿真结果表明该算法具有快速、精确和全局稳定的良好特性 .
1 移动舞台机器人轨迹跟踪问题描述
移动舞台机器人轨迹跟踪问题的本质是设计状态反馈控制律,使得移动机器人从任意初始位置出发,在满足移动过程中约束条件的同时,能够跟随预先设定好的期望轨迹.


图1 舞台移动机器人位姿示意图Fig.1 The location diagram of stage mobile robot
假设移动舞台机器人在侧向上不打滑,即其不能沿着驱动轮轴线的方向运动,故机器人沿驱动轮轴线方向的速度为零,满足纯滚动无滑动的非完整约束,即
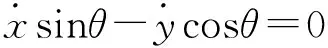
(1)
从而得到移动舞台机器人的运动学模型为

(2)

(3)
则位姿误差可以表示为
(4)
从而得到位姿误差动力学方程为
(5)
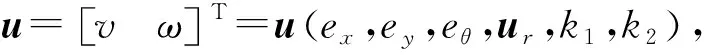
2 移动舞台机器人轨迹跟踪控制器设计
考虑随时间变化的控制系统[18],即

(6)
式中:f,g分别为R+×Rn到Rn的光滑映射.
定义1考虑非线性系统式(6),如果存在径向无界的正定函数V(x),对所有非零的状态变量满足
infLfV(x)+LgV(x)<0 ∀x≠0
(7)
则V(x)称为该系统的一个Lyapunov函数.式(7)意味着总是存在一个控制u使V(x)沿闭环系统轨迹是递减的,从而V(x)可以作为闭环系统的一个Lyapunov函数.
定义2如果存在一个Lyapunov函数V满足
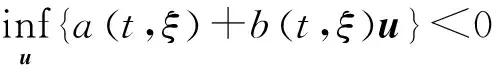
(8)

结合移动舞台机器人误差系统模型式(5),根据定义1,2可以容易地选择一个CLF候选函数并验证其有效性.选择一组二次型正定函数,即
(9)
作为时变系统的一个候选控制Lyapunov函数.
基于移动舞台机器人位姿误差方程式(5),设计一个非线性状态反馈控制律,其表达式为
(10)
其中可调参数k1>0,k2>0,并令K=[k1k2].从而获得闭环系统,即
(11)
式(11)可以表示成紧凑型,即

(12)
沿着系统式(11)的轨迹,把控制律式(10)带入二次型正定函数式(9),整理得它关于时间的导数为
(13)
显然,对可调参数任意取值满足k1>0,k2>0,V(x)沿闭环系统轨迹是递减的.根据定义1可知:式(9)是移动舞台机器人系统的一个控制Lyapunov函数,从而可以用来设计一个渐近稳定的控制律,即
(14)
从式(14)中的最后一行可以看出:a(t,x)+b(t,x)u<0恒成立,即满足定义2,表明移动舞台机器人误差系统是渐近稳定的.
理论上讲,控制律中k1,k2只要大于零就能保证系统的全局稳定性,但在仿真过程中发现K值的变化对整个系统的跟踪效果(收敛速度和误差的大小)影响比较大,且对不同的曲线需要重新设定K的值,若参数选择不当,可能会出现违反约束的情况,使移动舞台机器人在运动的过程中产生危险,达不到舞台效果.虽然通过人工调整可以达到预期效果,但耗时耗力,要经过多次试凑才可以得到最优参数.为了解决这些问题,利用MPC方法对控制器参数K进行优化计算,通过降低在线计算维数,提高了MPC求解算法实施的快速性,使得预测控制器在具有一定自适应性的同时降低了MPC的计算量.因此对这两个参数值进行优化是必要的.
以可调控制律式(10)作为移动舞台机器人的轨迹跟踪稳定控制类[19],记为h=(x,K).考虑移动舞台机器人的状态区间约束和控制区间约束分别为
(15)
(16)
利用CLF函数式(9)和预测控制律式(10)计算移动舞台机器人的最大不变集Ω为
Ω(c)={x∈R3|V(x)≤c}⊆S(x)
(17)
显然,集Ω的大小与控制约束和可调参数K的取值有关,但通常不易精确求解.因此,为了最大限度的得到Ω范围,离线求解如下多参数规划问题,获得常数c的最大值为
(18)
以及对应解Kmax.
为提高移动舞台机器人轨迹跟踪的最优性,考虑与系统输入输出状态有关的性能指标函数J(x,u),即
(19)
式中:Q,R分别为权重矩阵;T为常数,T>0为预测时域.
考虑状态反馈控制,在预测中利用系统误差模型式(11)和当前状态,迭代计算预测得到状态.具体步骤如下:
步骤0设计约束系统的稳定控制类h=(x,K),并离线求解式(18)得到闭环系统的最大不变集Ω,其中极值为cmax和相应的解为Kmax.
步骤1输入优化设计参数(x(t),T,Ω,Q,R).
步骤2在线求解移动舞台机器人轨迹跟踪MPC的在线优化问题,即

(20)
其中x(t)为当前时刻t的状态测量值.
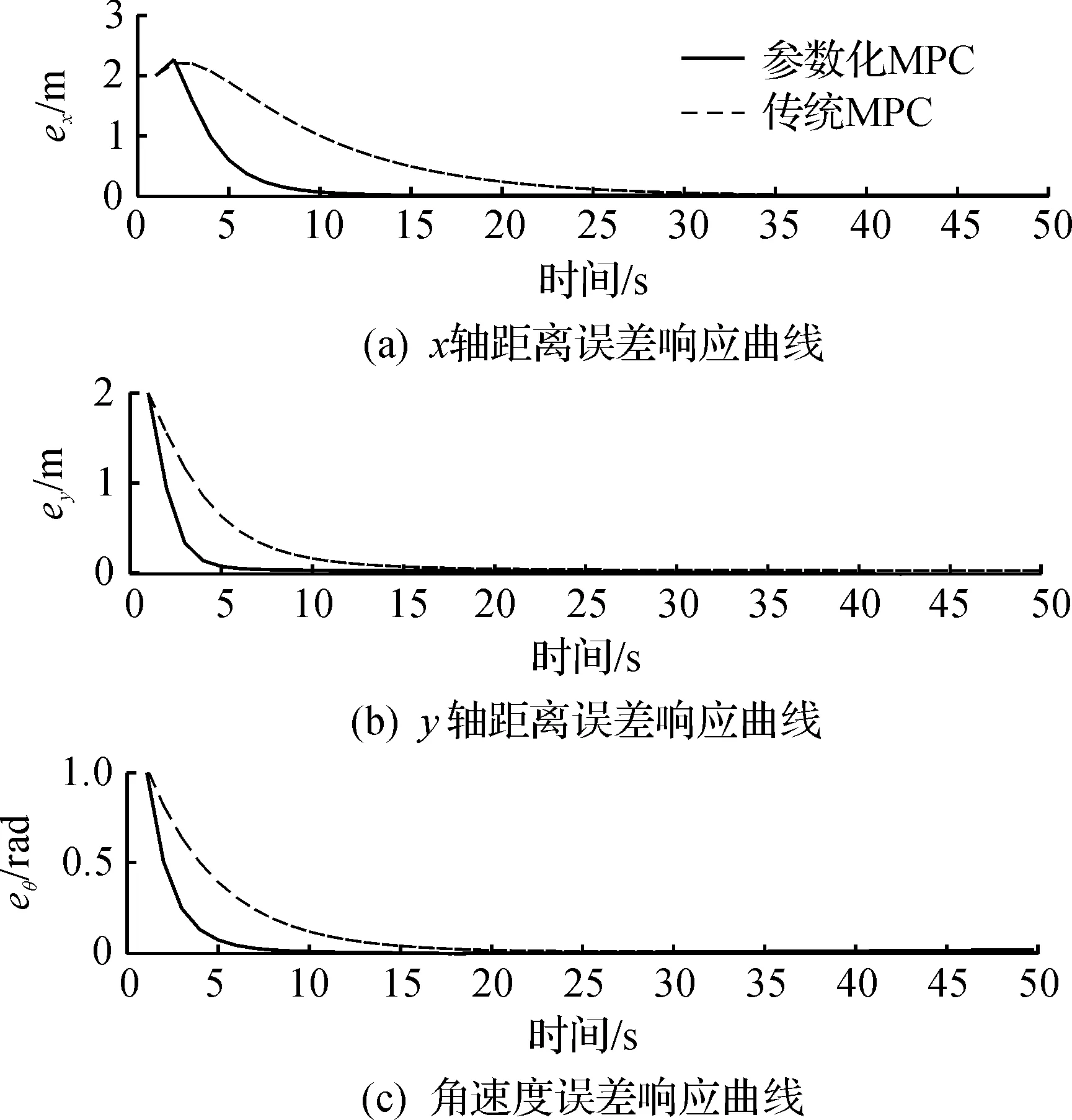
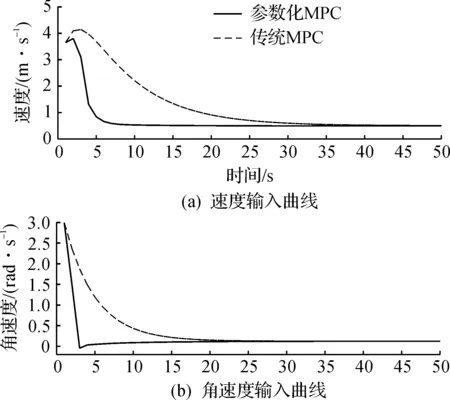
步骤3令常数0<δ (21) (22) 并令t=t+δ,返回步骤2. 对于移动舞台机器人系统及上述控制器,有如下稳定性结论. 定理假设对于任意初始状态,移动舞台机器人误差系统式(5)的解存在且惟一.那么对于充分小的采样周期δ>0,移动舞台机器人系统式(5)和MPC控制器式(21)组成的闭环系统在集合Ω上是渐近稳定的,且Ω是该移动舞台机器人闭环系统的一个稳定操作域. 证明由集Ω的计算方法可知:初始值Kmax对应的控制律h=(x,Kmax)总是满足移动舞台机器人误差系统的状态和控制量约束,从而Kmax为MPC优化问题式(20)的一个可行解,即对任意采样时刻t,以上优化问题总是可行的.考虑到V(x)是误差系统式(5)的已知CLF,当把控制器式(10)代入系统式(5)时,由定义2可知:V(x)为移动舞台机器人误差系统的控制Lyapunov函数,从而系统在集Ω上是渐近稳定的.又因为V(x)在每个采样期间内的严格单调递减性,集Ω是误差系统的不变集,所以Ω也是该移动舞台机器人系统的一个吸引域,即稳定操作域. 传统的MPC是对控制量直接优化,其决策变量和预测时域有关;而参数化MPC是对预测控制变量作有限维参数化[17],将对控制变量的直接优化转化为对控制器参数K的间接优化,从而可以降低MPC在线计算的维数,提高MPC求解算法实施的快速性.针对这两种控制方法,在Matlab平台上进行数值仿真验证. 仿真中,令期望的参考速度为vr=0.5 m/s,ωr=0.125 rad/s,期望参考轨迹为xr(t)=(vr/ωr)·sin(ωrt),yr(t)=-(vr/ωr)cos(ωrt)+4,θr(t)=ωrt,期望参考轨迹的初始条件为xr(0)=yr(0)=θr(0)=0.利用Euler法近似离散化舞台移动机器人位姿误差模型式(5),其中离散化时间δ=0.1 s,预测时域T=5,取WMR的初始条件为x(0)=-2,y(0)=-2,θ(0)=-π/3.权重矩阵Q=diag[1,1,0.5],R=diag[1,1,1].控制变量的约束为vmin=0,vmax=4.5 m/s,ωmin=0,ωmax=3 rad/s.控制器参数初始值为k1=0.8,k2=0.5.仿真结果如图2所示. 图2 移动舞台机器人运动轨迹曲线Fig.2 The moving track curve of mobile stage robot 在图2中,实线为参考轨迹,点划线对应的为参数化MPC方法的控制结果,虚线对应的为传统MPC方法在控制器参数值为k1=1.4,k2=1时的控制结果.由图2可知:在2种控制作用下,移动舞台机器人都能够跟踪到目标轨迹,即误差变量收敛至零.虽然所提出的参数化MPC算法与传统MPC方法都取得了良好的控制效果,但是在参数化MPC算法中,单步计算用时是0.04 s,而利用传统MPC方法用时0.082 s.由于控制周期是0.1 s,所以两种方法都能满足控制实时性要求,但是参数化MPC方法的效率提高了2倍左右.并且由于参数化MPC方法中的计算时间远小于控制周期,所以可以得到最优的控制器参数.另外,将保证闭环系统稳定的K的取值范围提前作为优化问题约束,所以即使是次优的K,同样可以保证闭环系统的稳定性. 图3 状态变量响应曲线Fig.3 The State variable response curve 图4 控制输入曲线Fig.4 The Control input curve 在图3,4中,实线表示参数化MPC方法的控制效果,虚线表示传统MPC方法的控制效果.仿真结果表明:随着状态误差变量趋于零,移动舞台机器人的线速度和角速度在满足约束的条件下都趋于参考值,但参数化MPC方法可以更加快速、稳定的达到目标. 最后,图5中给出了所提参数化MPC方法中在线优化的控制器参数变化曲线.图5表明:最优的可调参数根据移动舞台机器人的实际运行状态不断调整,从而使移动舞台机器人的运动效果达到指定性能的最佳要求. 图5 控制输入曲线Fig.5 The adjustable parameter change curve 考虑移动舞台机器人带约束的的轨迹跟踪控制问题,针对笛卡尔坐标系下移动舞台机器人位姿误差模型,提出了一种参数化MPC算法来实现移动舞台机器人的运动控制.参数化MPC算法通过在线滚动优化给定的性能指标,计算控制器的可调参数,把对控制量的直接优化转变为对控制器参数的优化,降低了决策变量的维数,提高算法实施的快速性.仿真结果表明:优化控制器参数可以在保证所设计的控制器具有一定自适应性的同时,使移动舞台机器人可以快速、精确的跟踪到目标轨迹,具有全局稳定的良好特性.
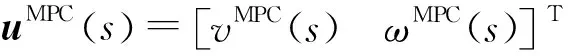
3 仿真结果与分析


4 结 论
