基于灰色理论的沥青混合料级配变异性分析

周争菊

（贵州省交通建设工程质量监督局，贵州 贵阳 550081）

0 引 言

沥青混合料配合比经过设计能够满足道路工程要求，然而在生产和施工过程中的操作误差会导致混合料级配发生变化，与设计级配发生偏离，则无法达到路面的使用预期，极大地影响路面的使用寿命［1］。在一定程度范围内的级配变异是可以接受的，在生产和施工过程中需要做到的是尽量减小级配的变异性。杨博等基于均匀设计理论，对设计级配以及变异级配的曲线包络面积进行统计计算，得到级配变异的评价指标［2］。黄继成等基于分形理论研究了集料级配的分形特性，并将其与混合料的路用性能建立联系［3］。相关研究也表明，利用分形理论研究级配分形特性与混合料的路用性能确实可行［4-6］。因此，分形理论在研究混合料级配时表现出的优势逐渐得到越来越多人的重视，但仅通过分形理论研究混合料设计级配与实际生产级配之间的差异是不够的，寻找导致级配变异发生的影响因素并进行控制是最重要的［7-8］。孟利强在研究混合料级配变异评价及控制手段发展的基础上，基于灰色理论利用各筛孔通过率这一指标评估了混合料生产时级配变化［9］。修海军等也采用灰色理论分析了各筛孔通过率与路面施工质量的关系，并得到了施工质量的级配控制技术［10］。

本文对混合料生产拌合站的级配进行抽样检查，通过分形理论研究生产级配与设计级配之间的变异性，基于灰色理论研究各料仓投放集料时对级配变异产生的影响，从而得到关键的粒径级料仓，控制级配变异，确保混合料级配尽可能与设计级配的偏差较小，保证道路的设计服务性能以及施工质量。

1 级配分维数计算

分形理论在描述几何形体以及空间填充等方面具有特有的优势，在对无规则、无序及不稳定性现象的研究方面得到了广泛应用［11-12］。基于分形理论的集料级配领域的相关研究表明，集料的拓扑维数为3，集料的质量分布与分维数具有如下关系。

式中：P（r）为粒径为r的集料的质量通过百分率；D为分维数；r为筛孔尺寸；rmin为最小粒径尺寸；rmax为最大粒径尺寸。

在实际工程中，混合料级配中的最小粒径一般极小，可忽略不计，即令rmin=0，则式（1）可表达为

两边同时取对数，得到

在双对数坐标上对级配曲线进行拟合，集料级配双对数曲线斜率K与分维数D有如下关系。

不同混合料级配的分形特征可通过其分维数表征，不同的级配对应不同的分维数D。因此，设计级配和实际生产时拌合楼的级配分别对应不同的分维数，如果两者较为接近，理论上两者的级配趋于一致，即两者的级配较为相似；相反，如果两者差别较大，则说明生产的级配发生了离析变异，导致生产级配和设计级配有较大差异。所以，可以通过设计级配和生产级配的分维数差值来表征级配的变异性，分维数差值计算如下

式中：d为分维数差值；D0为设计级配分维数；D1为生产级配某次检测的分维数。

2 级配变异性评价

2.1 基于分维数差值评价级配变异

在拌合站对SMA-13混合料进行抽样检查，通过过筛确定生产级配各筛孔的通过率。混合料的设计级配和现场抽检的级配如表1所示，根据分维数的计算方法对两次抽样检测级配进行分维数差值计算。根据式（3）对表1的数据进行拟合，结果如图1和表2所示。

表1 混合料级配

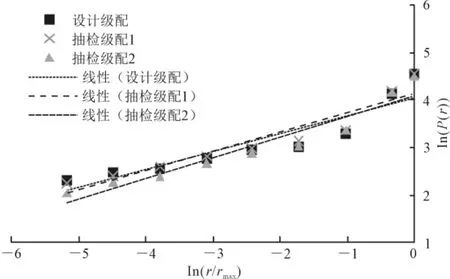
图1 质量分布与粒径比的双对数关系

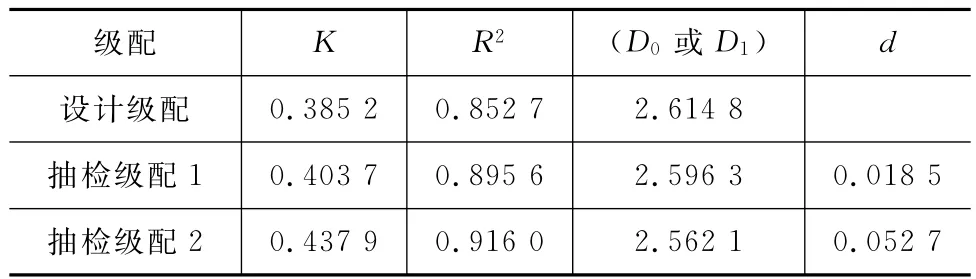
表2 分维数差值计算结果

作为能够反映级配性质的R2，其值与级配类型有关，连续级配在双对数坐标中具有较好的线性，拟合效果相对较好，因此一般R2较大；而间断级配较为分散，黏合效果较差，R2相对较小。SMA-13是一种间断密实级配，因此设计级配的拟合相关性表现一般，由图1及表2可知，抽检级配1与设计级配更为接近，抽检级配2的相关性好于其他两者，但其级配不如抽检级配1与设计级配的相似性好。以设计级配的分维数为基准，对比2个抽检级配分维数与设计级配分维数的差值可以发现，抽检级配1的分维数差值为0.018 5，抽检级配2的分维数差值为0.052 7。结合图1可知，抽检级配1与设计级配更为接近，抽检级配2与设计级配发生相对明显的变异，反映在分维数差值上，就是分维数差值越大变异越显著。

2.2 级配变异性评价

对实际工程混合料生产拌合楼的级配进行检测时，抽样检测几组并不能完全反映所检测级配的变异性，因此采用大样本抽样，针对一种级配抽样检测100组数据，基于设计级配进行100组检测级配的分维数差值计算，分析分维数差值的分布规律和反映检测级配的可信程度，进而对生产级配相对于设计级配的变异性进行评价。

在拌合站对SMA-13混合料级配进行100次抽样检测，根据设计级配和检测级配的分维数进行差值计算，对其排序处理后得到图2结果。

图2 SMA-13级配抽检分维数差值

对抽检的100组级配进行双对数曲线拟合，相关系数均大于0.8，认为拟合可信。由图2可见，分维数差值基本都小于0.02，存在一个未超过0.03的极大值。鉴于误差的随机性，对本次抽样检测的数据进行数理统计分析，利用SPSS软件通过Kolmogorov-Smirnov（K-S）进行数据检验，结果如表3所示。

通过K-S检验数据可以看出，渐进显著性为0.998，大于0.1，说明本次抽样检测计算得到的分维数差值数据服从N（0.010 9，0.005 62）的正态分布，如图3所示。

由图3可见，频率直方图与正态分布曲线符合性较好，抽检级配的分维数差值的分布基本符合均值μ=0.010 9、方差σ=0.005 62的正态分布。基于连续化处理离散的数据，对于没有离析的级配，理想情况下检测到的分形维数差值应该分布在0附近。然而，实际工程同组混合料离析的检测中系统误差、测量误差不可避免，且系统误差具有方向性，量值确定；而测量误差不具有方向性，量值随机，所以分维数一般会同时普遍大于或小于设计级配，求其绝对误差更加合理。以实测概率分布为依据，取置信度为95%，对均值进行区间估计，即分维数差值的均值μ的置信区间为（0.009 3，0.012 5），即在置信度为95%的情况下，图像检测级配分维数差值均值μ＜0.012 5时，认为其没有离析或离析程度较轻。本次抽样检测100组数据级配的分维数均值为0.010 9，可以推断调查抽样的该次生产级配并没有严重偏离设计级配。

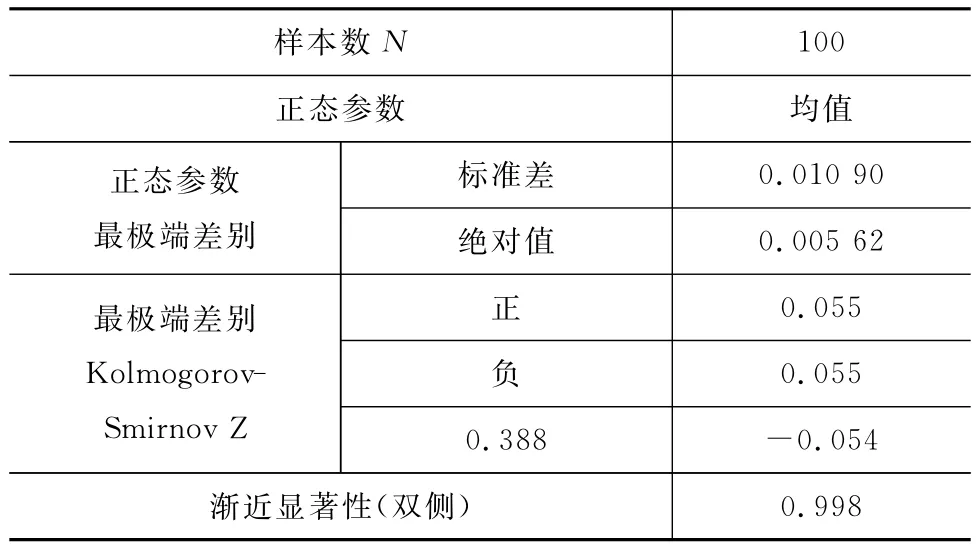
表3 SMA-13数据检验

图3 SMA-13抽检级配分维数概率分布

3 级配变异性的影响因素分析

在实际工程中，混合料通过各档料仓进料，搅拌后完成配比，因此各档粒径级的料仓的供料直接影响着混合料的级配变异性。各档集料料仓的供料占比不同，对级配变异性的影响也存在差异，找到影响级配产生变异的关键粒径级，对控制级配变异性至关重要。

3.1 灰色理论

灰色关联分析基本原理是通过确定参考序列数据和若干个比较序列数据的几何形状相似程度来判断其联系是否紧密，它反映了曲线间的关联程度。序列曲线几何形状越接近，它们的变化趋势越接近，其关联度就越大，反之就越小。关联度的计算过程如下。

比较 序 列 数据 Xi（j）=｛Xi（1），Xi（2），…，Xi（m）｝，i=1，2，…n；j=1，2，…，m。其中，n代表影响因素数量；m代表各影响因素的评价指标的数量。参考 序 列 数 据 为 X0（j）=｛X0（1），X0（2），…，X0（m）｝。对各序列数据按照下式进行无量钢化处理。

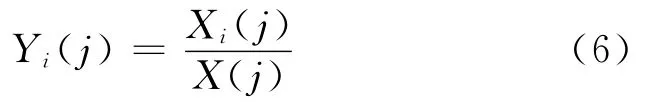
当ρ取0.5时，γi≥0.6时子母因素有关联；γi＜0.6则认为关联性较差；γi＜0.5认为无关联。两序列的关联度可用2个比较序列各因素的关联系数之平均值计算，即

3.2 粒径组对级配变异性的影响

灰色理论可以很好地定量分析各粒径级集料对级配变异产生的影响。以计算得到的级配分维数差值作为参考序列，各粒径组含量作为若干个比较序列，对比参考序列和比较序列之间的关联系数和关联度，通过寻求系统中各因素间的主要关系找出影响目标值的重要因素，最终确定影响级配变异的关键粒径组。结合各级配粒径组含量数据及对应的级配分维数，以各粒径组集料含量为变量Xi（j），级配分维数为X0（j）。

对SMA-13抽样检测的数据进行均值处理，10个1组，得到共10组数据。将SMA-13各粒径组的集料含量 X1（0.075～0.15mm）、X2（0.15～0.3 mm）、X3（0.3～0.6mm）、X4（0.6～1.18mm）、X5（1.18～2.36mm）、X6（2.36～4.75mm）、X7（4.75～9.5mm）、X8（9.5～13.2mm）、X9（13.2～16mm）作为比较序列，计算得到的级配分维数差作为参考序列（记为X0），得到级配分维数差值与粒径组含量，如表4所示，无量纲化处理后得到表5中的数据，基于参考序列得到各个比较序列的差值，如表6所示。其中，通过式（7）计算关联系数，结果如表7所示，最终得到各粒径组与级配分维数的关联度，如表8所示。

表4 级配分维数差值与粒径组集料含量

由表8可见，各粒径组与级配分维数的关联度均大于0.7，说明各粒径组集料含量与拌合楼生产混合料的级配分维数差值均有关联，即各粒径组集料含量对级配的变异性均产生影响，关联度排序为γ1＞γ4＞γ3＞γ2＞γ5＞γ9＞γ7＞γ8＞γ6，对应的各料径组对SMA-13设计级配变异产生的影响从大到小依次为0.075～0.15mm、0.6～1.18mm、0.3～0.6 mm、0.15～0.3mm、1.18～2.36mm、13.2～16mm、4.75～9.5mm、9.5～13.2mm、2.36～4.75mm。按照相关规范对粗细集料的划分，计算得到2.36 mm及以下细集料关联度系数均值和粗集料关联度系数均值分别为0.723 1、0.721 2，即对于SMA-13级配而言，细集料对其级配变异的影响要大于粗集料。

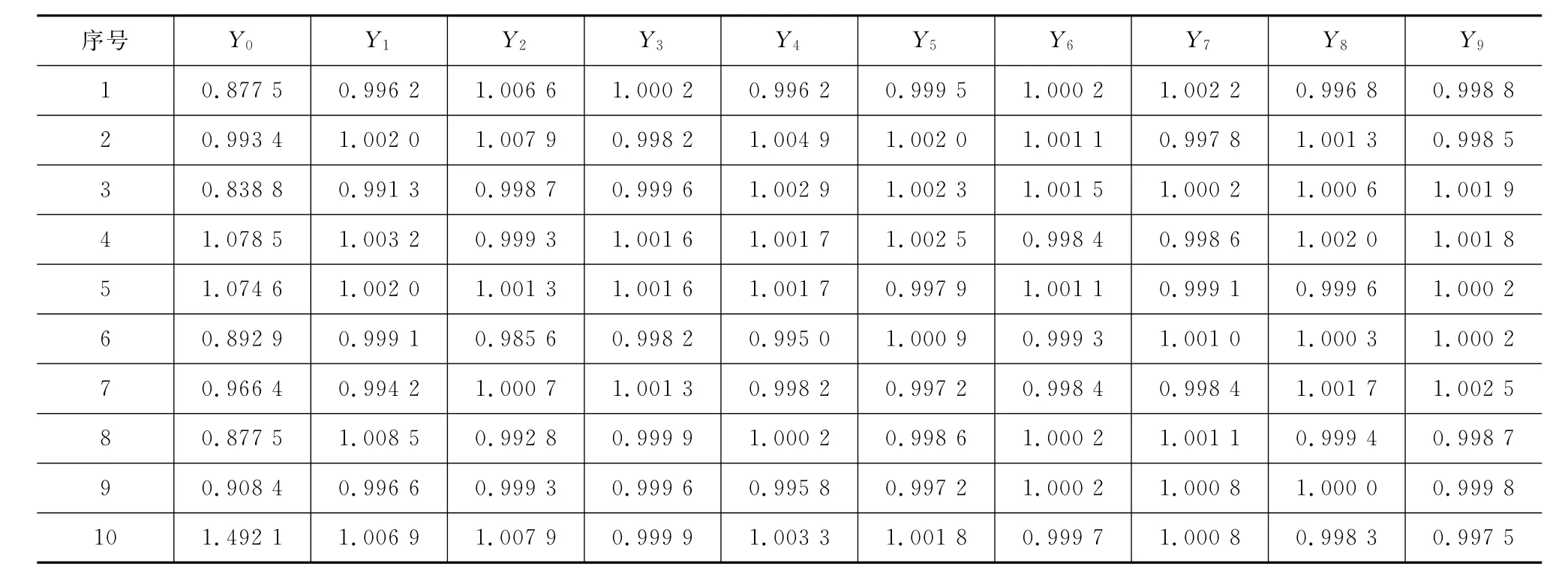
表5 无量纲化处理

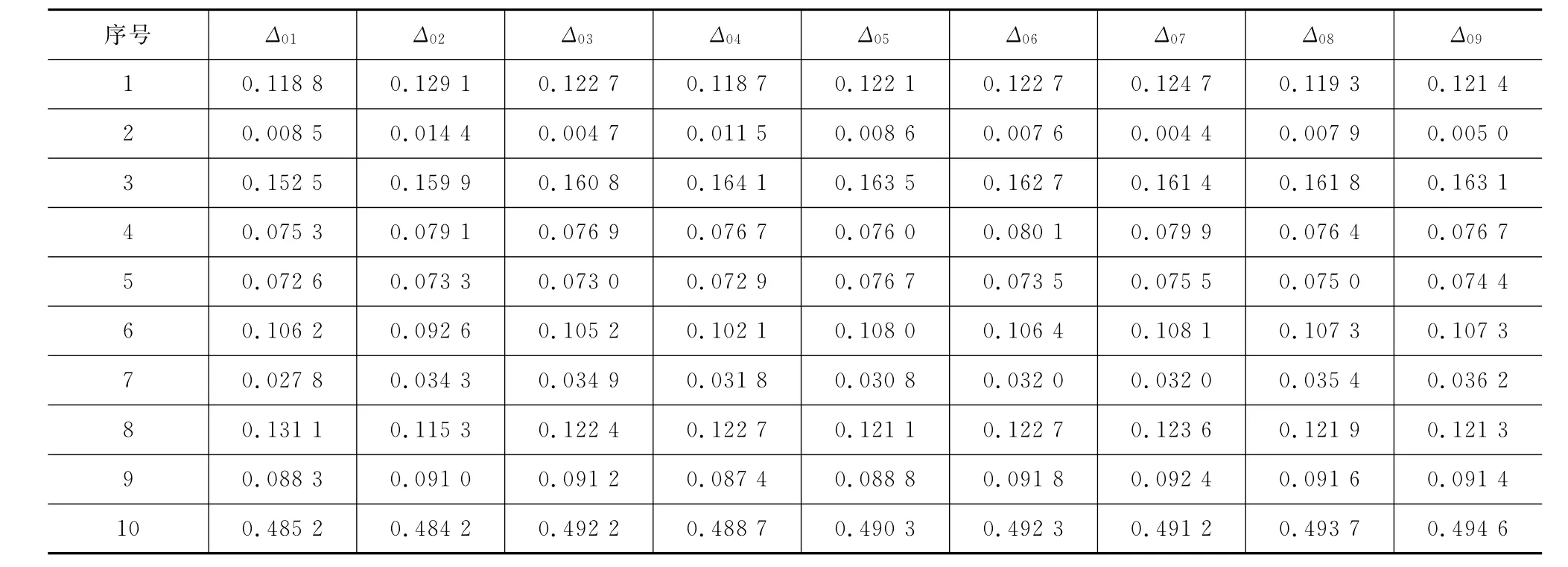
表6 对比序列绝对差

表7 关联度系数

4 结 语

（1）基于分形理论，通过分形维数对设计级配的变异性进行表征，通过对拌合站生产级配的大样本抽检，发现大样本抽检得到的级配分维数差值符合正态分布，在置信度为95%的情况下，分维数差值可较好地评价级配的变异性。

（2）基于级配的分维数差值计算，对生产级配的各料仓供给料粒径组进行灰色关联分析，得到各粒径组与级配分维数差值关联度均大于0.7，认为各粒径组集料对级配变异均有影响。对于SMA-13级配而言，细集料对其级配变异影响较大，在生产施工时要注意控制细集料的投放，尤其是0.075～0.15mm和0.6～1.18mm两档集料，鉴于生产时该两组粒径的集料往往源自同一个料仓，因此具体如何改善并控制级配的变异性有待进一步研究。