关注学生，成就精彩

江苏省徐州市桃园路小学 杨春燕

一节好课的标准有很多，精心的教学设计、融洽的课堂氛围、组织得当的教学过程、精准的课堂评价……除了这些，还有一个很重要的方面，那就是学生的参与度与学习状态。教师在课堂上要密切关注学生的学习情况，把学生放在主体地位。《数学课程标准（2011年版）》指出：“有效的数学教学活动是教师教与学生学的统一，应体现‘以人为本’的理念，促进学生的全面发展。”今天，我们就把目光聚焦到学生身上，关注学生的“学”，看看在哪些方面需要老师们在以后的教学中持续关注，从而提升课堂教学品质。

一、关注学生错误，凸显知识系统

学生在学习知识的过程中出现错误是不可避免的，在任何学科知识的学习中都会遇到。作为教师，如何对待学生出现的错误显得尤为重要。是含糊其词、听之任之，还是简单粗暴的否定、草草了之？不同的处理方式会带来不同的学习效果。我想，有经验的老师会用心倾听学生的错误，冷静思考，因势利导，抓住出错点重新构建新问题，带领学生再思考、再讨论，在帮助学生纠错的同时提升学生对新知的认知水平，有效帮助学生梳理出知识系统。

例如，在六年级期末复习课《平面图形的周长与面积》一课教学中，老师给学生出示了探究要求：（1）根据整理单梳理面积公式推导过程，说说公式是怎样推导出来的。（2）让学生利用平面图形公式推导的过程，用六个图形模型、箭头、连线等设计思维导图。学生在探究之后，各小组都完成了一份思维导图。教师随机选取两个小组的代表到黑板上展示，其中一个小组的思维导图是这样的：

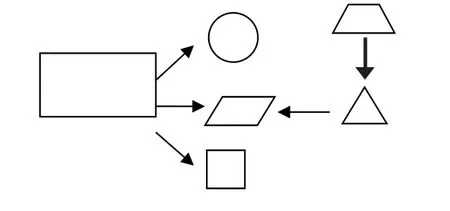
在汇报的时候，两个小组由于设计的思维导图不同，所以汇报也不同，争议就在梯形、三角形和平行四边形之间的关系上。由于学生已经到了六年级下学期的期末复习，对这六种平面图形已经有了系统的学习和了解，所以在汇报时头头是道。这个时候，面对出现的错误，老师不动声色地提问：“同学们观察一下，这一组的思维导图和刚才那一个有何不同？”一下子把大家的目光集中到这两组不同的思维导图上来。老师不再发问，把课堂留给学生，有了对比，才有发现。静静地观察一分钟后，孩子们马上发现平行四边形和三角形及梯形之间的箭头方向不同，但是不敢肯定地说出哪种是正确的。于是，老师因势必利导，让这一组的学生说说是怎样想的，这种思路是怎么得来的。

生1：梯形可以分成两个三角形，所以由梯形的面积公式可以推导出三角形的面积公式，而两个三角形又能拼成一个平行四边形，所以由三角形的面积公式又可以推导出平行四边形的面积公式。

他的这一次解释，真是一石激起千层浪，下面马上炸开了锅，不断有学生争先恐后地举起高高的小手，大家争着给他纠正错误。在听取了几个同学的“批评指正”之后，老师追问：“到底是由梯形的面积公式推导出三角形的面积公式，还是由三角形推导出梯形的面积公式呢？”这一次追问又一次把学生们推向了高潮，孩子们激烈地讨论着，最后达成共识：是由平行四边形推导出三角形和梯形的面积公式。

课上到这儿，好像已经真相大白了，但是老师没有止步，而是又一次叫起了刚才汇报的学生，请他再来谈一谈。

生1：刚才的思维导图线路的顺序出错了，箭头的方向应该调整。

师：哦，是吗？那请你上来重新调整一下吧。

……

掌声不约而同地响起来。

教师巧妙利用学生的“错误”，放大出错点，抛出新问题，引导学生再思考、再讨论，在思辨的过程中帮助学生构建知识系统，赋予课堂新的活力与生机。

二、关注学生生成，提升课堂品质

教学的预设与生成，是一对矛盾体。“生成”是新课程倡导的一个重要理念。叶澜教授曾说过：“一节课不能完全是预设的，一定要有生成性。”每节课上，都可能会遇到学生的回答在预设之外的情况，这些偶发事件常常会让老师措手不及。面对这种情况，我们做教师的要静下心来，抓住“生成”的资源，有可能就会成就课堂中的“亮点”。

例如，在《圆柱圆锥》的复习课上，老师请学生思考：用平面图形能想办法得到圆柱和圆锥吗？要求：独立想一想，动手做一做，组内说一说。

大部分学生是这样汇报的：方法一：旋转。用长方形沿着长或宽旋转一周；用直角三角形围绕着直角边旋转一周。方法二：围。拿出一张长方形纸，沿着长、宽围。

有一个学生的方法跟大家不一样，他拿着一个圆片演示，“可以把很多的圆片像这样压在一起，也可以得到一个圆柱。”

听到了他的回答，很多学生若有所思，似懂非懂。老师故作惊讶：“谁听懂了他的想法？这样也可以吗？”教室里一片沉默。师：“请你再来说一遍。”这次，很多学生好像听懂了，老师及时抓住这个“意外”追问：“看看这个圆叠加形成的圆柱，你能想到它的面积怎么计算吗？”有了刚才对叠加的理解，孩子们马上回答：可以用底面积乘高。教师继续追问：“什么样的图形向上叠加形成的轨迹也可以用底面积乘高？”有的同学想都没想就回答：“圆锥。”学生们立马议论开了：“圆锥不行，圆锥上边越往上越小。”在大家的问答中，孩子们进一步认清了圆锥的本质属性。经过讨论，大家知道了长方体、正方体和三棱柱也可以用底面积乘高来计算。

这次意外，虽然没有紧紧抓住课题围绕圆柱圆锥展开，看似跑偏了，但是却把孩子们的思维引向了更深入的思考，从另外一个角度辨析了圆柱和圆锥的特征和不同。正是因为教师敏锐捕捉到了课堂上的“生成”，才激发了学生们的学习兴趣，把课堂推向了高潮。

三、关注学生回答，及时跟进点拨

一节课上得是否有效，很大程度上取决于学生的参与度。每节课上，我们都会听到很多学生回答问题，这些回答是否准确，如何回应，我们做教师的不仅要用心倾听，更重要的是及时跟进与点拨。

例如，在教学“解决问题的策略——转化”时，在引导学生想办法比较两个图形的面积大小之后，教师提问：“想一想，刚才是怎样比较两个图形面积大小的？用了什么样的方法？”引导学生回顾刚才是用转化的方法比较的。教师继续提问：“在转化的过程中，什么变了？什么没变？”学生们经过简单的思考得出：图形的形状变了，面积大小没变。一般情况下，教学到这里就可以进入下一环节了，学生们不仅探究出用转化的方法去比较两个图形面积的大小，而且认识到在转化的过程中有些变了，有些没变，然而老师继续追问：“形状是怎么变化的？怎么知道面积没变的？”学生会重新审视变化前和变化后的图形，在思考的过程中体会到转化的妙处。

进一步的追问会走向定量描述，帮助学生找出图形间的形状变化关系，找到转化变化中不变的面积关系。

要上好数学课，不是一件简单的事情。关注学生，需要一种智慧，关注学生的错误、关注学生的生成、关注学生的回答，把思维的主动权还给学生，才能成就课堂的精彩。