Maurer通用统计检测的优化实现研究*

康红娟，杨先伟，张文科

（1.四川长虹电器股份有限公司，四川 成都 610041；2.无锡职业技术学院，江苏 无锡 214121；3.成都卫士通信息产业股份有限公司，四川 成都 610041）

0 引 言

习近平主席在2014年指出，没有网络安全就没有国家安全，网络安全已经上升到国家战略。网络安全主要包括信息的机密性、完整性、可鉴别性、不可抵赖性以及访问控制等。实现这些的重要手段是密码技术，而众多密码技术的一个共同之处是要实现随机化，如密钥、初始化向量、数字签名等都必须是密码学安全的随机数。由此可见，随机数不论在密码工程还是在密码理论方面，都有着举足轻重的地位和作用。随机性检测是采用概率统计的方法对随机数发生器等生成的二元序列进行分析和测试，判断待检序列是否在统计上难以与真随机数区分开来。不同的随机性检测算法从不同的角度分析测试待检序列与真随机序列的差异。随机性检测算法经过多年的发展已经取得了丰硕的研究成果，目前有大量的随机性检测算法和检测工具，而且有很多新的随机性检测算法还在源源不断地涌现。美国国家标准与技术研究院（National Institute of StandardsAnd Technology，NIST）发布并反复修订了文档SP 800-22[1]，其中共建议了15种用于随机性测试的统计检验方法。德国以此为基础发布了BSIAIS 30规范[2]。我国国家密码管理局于2009年颁布了我国的随机性检测规范[3]，其中建议了15种随机性测试的统计检验方法。此外，还有很多别的著名检测标准和工具，如Diehard、TestU01、ENT和CryptX等。

随机性检测在实际应用中有着广泛应用，如测评按照特定标准生成的伪随机数据；检测密码算法生成的数据流，如分组算法生成的数据流[4]；以杂凑算法如我国的SM3杂凑算法[5]为核心生成的数据流。这些检测可以为算法分析者提供帮助，减少工作强度，同时能够检测出其他测试方法难以检出的安全隐患。

NIST统计测试套件（NIST STS）[6]实现了NIST随机性检测规范描述的所有检测项目。传统的检测通常使用此NIST STS随机性测试代码和工具进行检测，但其检测效率非常低。因此，大量的学者进行随机性检测规范的各个检测项的快速现实研究。比如，扑克检测的快速实现研究[7]、单比特检测和块内频数检测的优化实现研究[8]。也有学者设计新的统计测试方法作为随机性检测规范的补充[9]，还有学者研究统计测试算法的基于GPU的并行实现，并构建并行实现的统计测试框架[10]，以及分析线性复杂度检测、B-M算法优化检测[11]等。

SuciuA等[12]采用基于字节处理的方式，显著改善了Maurer通用统计检测的执行效率。文献[13-15]在此研究成果的基础上，对实现方式和代码做了进一步优化，使得效率提升了42.2%。本文在文献[13]的基础上，对其中的Maurer通用统计检测进行多角度综合优化，从整体上改善Maurer通用统计检测的效率，以提升整个国密随机性检测的检测速度。

文章结构组织如下：第1节简单介绍Maurer通用统计检测的执行流程；第2节分析Maurer通用统计检测的思路，并讨论进一步优化的可行性；第3节提出Maurer通用统计检测的快速实现算法；第4节测试优化算法的检测效率和速度提升情况；最后总结全文。

1 Maurer通用统计检测简介

NIST的随机性检测规范和我国的随机性检测规范都有15项检测，其中两者有11个相同的检测项，而Maurer通用统计检测是其中一项。此外，我国随机性检测规范有4个专有的检测项，NIST的随机性检测规范也有4个专有的检测项。

Maurer通用统计检测主要检测待检序列能否被无损压缩。如果待检序列能被显著压缩，则认为该序列是不随机的，因为随机序列是不能被显著压缩的。Maurer通用统计检测可以用来检测待检序列多个方面的特征，但并不意味着Maurer通用统计检测是几个检测的拼装。相反，Maurer通用统计检测采用了和别的检测完全不同的方法。一个序列可以通过Maurer通用统计检测，当且仅当这个序列是不可压缩的。

记 ε=ε1,ε2…εn为长度是 n 比特的待检二元序列，εi=(0,1)，1≤i≤n。我国的随机性检测规范取样本长度n为1×106bit。

α为显著水平。我国的随机性检测规范规定，显著水平α=0.01。

erfc是余差函数，定义为：

实际使用中，通常采用字节来存储随机序列。对这种以字节表示的随机序列，其Maurer通用统计检测的检测流程描述如下[3,13]。

算法1：Maurer通用统计检测算法

输入：n比特（ n ≡ 0 mod8）的待检二元序列ε=ε1,ε2…εn以字节表示为 ε=B0B1B2…BN-1，N=n/8。

输出：通过或者不通过Maurer通用统计检测

步骤1：将待检序列分成两个部分——初始序列和测试序列。初始序列和测试序列分布包括Q个和k个L位的非重叠子序列，多余的位舍弃，即不够组成一个完整的L位子序列的位舍弃，其中：

我国随机性检测规范规定L=7、Q=1 280。

步骤2：针对初始序列创建一个表T，它以L位值为表中的索引值，Tj(1≤j≤2L)表示表中第j个元素的值。计算：

其中j是初始序列中第i个L位子序列的十进制表示。

步骤3：计算sum。

其中，遍历完第i(Q+1≤i≤Q+K)个L位子序列后应更新Tj=i。

步骤4：计算V值。

步骤5：计算P值。

步骤6：如果P-value≥α，则认为待检序列通过离散傅立叶检测。

Maurer通用统计检测的示意图见图1，其中描述了初始序列、测试序列和末尾丢弃数据等。

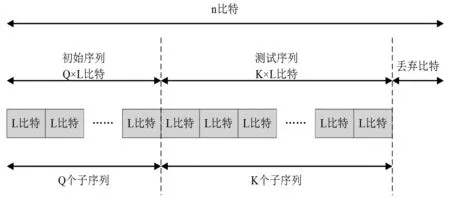
图1 Maurer通用统计检测

2 优化实现思路

Maurer通用统计检测需要的数据量很大，将序列分成长度为L的子序列，然后将待检序列分成两部分——初始序列和检测序列。初始序列包括Q个子序列，Q应该大于等于10×2L；检测序列包括K个子序列，K应该大于等于1 000×2L。L的取值范围为1≤L≤16，L取不小于6的值。Q的取值应该保证L位子序列的所有2L个模式都在初始序列中至少出现一次。

从头开始遍历初始序列，找到每一个L位模式在初始序列中最后出现的位置（块号）。如果一个L位模式在初始序列中没有出现，那么将其位置设置为0。此后，从头开始遍历检测序列，每一次都会得到一个L位子序列，计算这个子序列所在的位置与其前面最后一次出现的位置差也就是块号相减，称相减结果为距离，再对距离求以2为底的对数，最后将所有求对数的结果相加。这样就可以得到统计值：

统计值fn应该渐进服从单边正态分布。我国随机性检测规范采用式（8）计算该期望值。

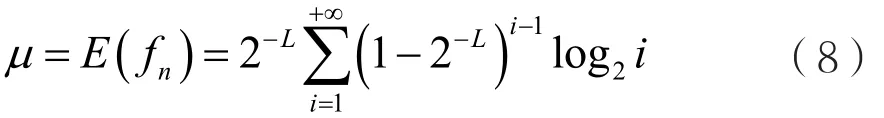
fn的期望值是随机变量log2G的期望值，其中G=GL是参数为1-2-L的几何分布。

σ的计算方式为：

这里c(L,K)是一个影响因子。我国随机性检测规范采用式（10）来估计：

统计值V=(Fn-E(L))/σ应该服从标准正态分布。

NIST统计测试套件（NIST STS）实现了NIST的随机性检测规范描述的所有检测项目，但是其中采用基于比特的处理方式使得Maurer通用统计检测的效率较低。文献[12]采用基于字节处理的方式显著改善了Maurer通用统计检测的执行效率。文献[13-15]在此基础上对代码做进一步优化，使得效率得到了进一步改善。

对以字节表示的待检序列，文献[13]优化方案中还存在如下不足和可以优化改进之处。

（1）该方案中虽考虑了以字节为基础进行处理，但没有充分考虑基于字节的优化，丢弃了很多可用的数据。

（2）步骤3中要执行K个log2D的计算，当n=1 000 000、L=7、Q=1 280时，K=141 577。大量的对数计算，是影响检测效率的另一个重要因素。

本节在文献[13]优化方案的基础上，对以字节表示的待检序列提出Maurer通用统计检测的如下优化改进思想。先定义如下名词和记号以方便描述。

定义1：N字节待检序列中任意连续的L个字节称为一个宏块，记为MB。

性质1：N字节待检序列ε=B0B1B2…BN-1按连续L个字节的宏块划分为：

①初始序列的宏块为：

在随机性检测规范中，L=7、Q=1 280。所以，初始序列按宏块划分无多余字节。

②测试序列的宏块为：

测试序列末尾共有NmodL字节，BN-Nmod7,…,BN-1无法凑足一个完整宏块。对n=1 000 000Bit的二元序列而言，测试序列末尾剩余1Byte无法凑足一个完整宏块。

性质2：每个宏块MBi,0≤i≤[N/L]都可拆分为8个L位非重叠子序列Ei,j,0≤i≤[N/L],0≤j＜8。

在不会造成歧义时，仍将非重叠子序列Ei,j的十进制表示为Ei,j。

Maurer通用统计检测的优化改进思想描述如下。

（1）无论是初始序列还是测试序列，按连续L个字节为一个宏块进行划分，每个宏块拆分为8个L比特非重叠子序列。对每个宏块的8个L比特子序列执行原算法的步骤2和步骤3，减少数据的加载以及加载数据被丢弃的情况。

（2）在执行步骤3时，为了减少对数的计算，将sum的计算简化为先对这8个子序列分别计算其十进制数与Tj的差值即距离，然后将这8个距离相乘，最后再对乘积计算对数，即采用以乘法换对数的方式。

3 优化算法

N字节的待检序列的优化实现的Maurer通用统计检测算法描述如下。

算法2：优化实现的Maurer通用统计检测算法

输入：N字节的待检序列以字节表示为ε=B0B1B2…BN-1。

输出：通过或者不通过Maurer通用统计检测

步骤1：初始化表值。将初始序列的每个宏块MBi,0≤i＜Q/8执行如下步骤：

（1）MBi拆分为8个L位非重叠子序列Ei,j，0≤j＜8；

（2）初始化表T：

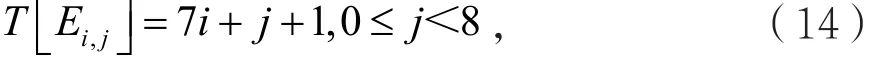
步骤2：初始化累加和sum=0。对测试序列的每个宏块MBi,Q/8≤i＜[N/L]执行如下步骤：

（1）将MBi拆分为8个L位非重叠子序列Ei,j，0≤j＜8；

（2）计算距离Dj=Li+j+1-T [Ei,j],0≤j＜8；

（3）更新表值T [Ei,j]=Li+j+1,0≤j＜8；

（5）更新累加和sum=sum+log2D。

步骤3：更新累加和sum。对测试序列的末尾不能构成完整宏块的数据Bi，N-NmodL≤i≤N-1，执行如下步骤：

（1）依次获取L位非重叠子序列Ei；

（2）更新累加和sum=sum+log2(i-T)；

（3）更新表值T [ j]=i。

步骤4：计算V值。

步骤5：计算P值。

步骤6：如果P-value≥α，则认为待检序列通过离散傅立叶检测。

考虑初始序列的计算复杂度，文献[13]方案需要Q次数据加载，但其实现中以UINT32加载且存在内存边界不对齐的情况，会导致数据加载效率降低。优化方案中，每L个字节的数据拆分8个L比特非重叠子序列，数据加载为L次字节加载，不存在内存边界不对齐的情况。考虑测试序列的计算复杂度，文献[13]方案计算sum时需要2K次数据加载、2K次加减法和K次对数。优化方案将L个字节的数据拆分8个LBit非重叠子序列时，数据加载次数同上；此外，8个子序列对数的计算次数也从原来的8次降低为1次，但需额外的8次乘法。综上，文献[13]方案和本文优化方案的计算量对比如表1所示。

表1 两种方案的运算量对比

4 实验与结果

本节对优化算法进行效率测试，并与文献[13]算法、NIST STS软件包的执行效率进行对比分析。

本文使用的测试平台信息如表2所示，所有测试均在此平台下进行。

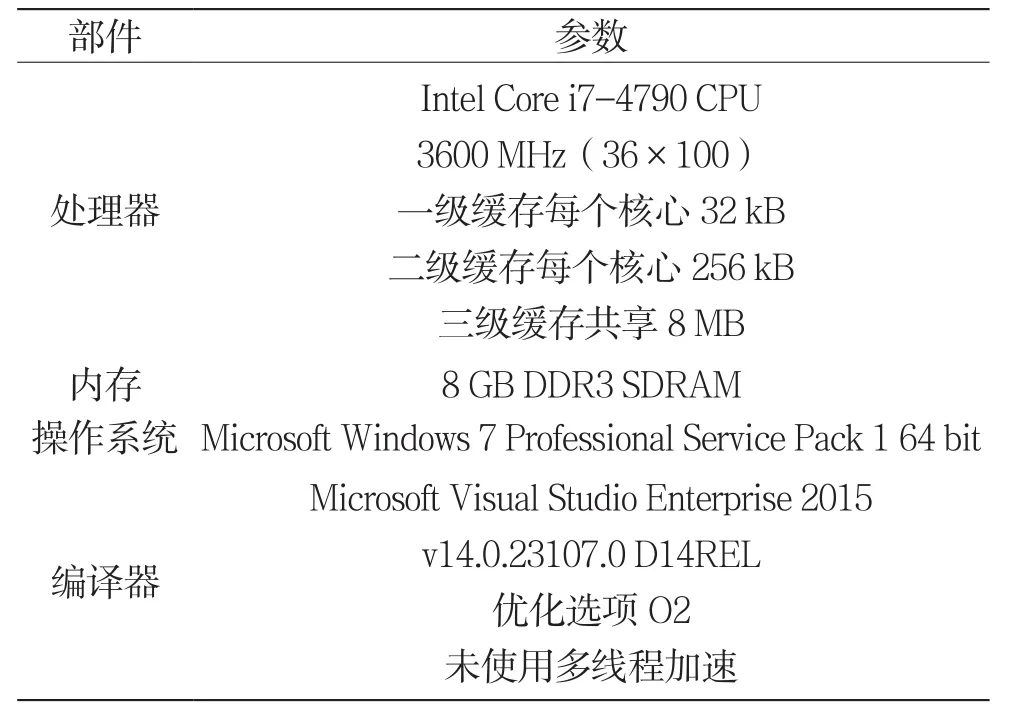
表2 测试平台信息

测试使用数据为SM3算法生成的伪随机数，按1×106bit为一个样本生成1 000个样本。

测试方法采用欧洲estream算法竞赛的速度测试模型的简化版本。主要执行流程为：反复测试待测代码段的耗时C次，并保存每次的耗时值T [i]，1≤i≤C。将耗时值序列按从大到小（或从小到大）的顺序排列，取新序列的中值作为本段代码的统计耗时值。本文:实验中将测试次数设置为51。测试使用的时间计数器为CPU频率计时器，直接调用纳秒级精度的RDTSC汇编指令，在Windows环境下调用函数rdtsc()。

Maurer通用统计检测进行检测的执行效率，如表3所示。

表3 优化前后的执行效率

三种Maurer通用统计检测的检测速度的柱状图如图2所示。

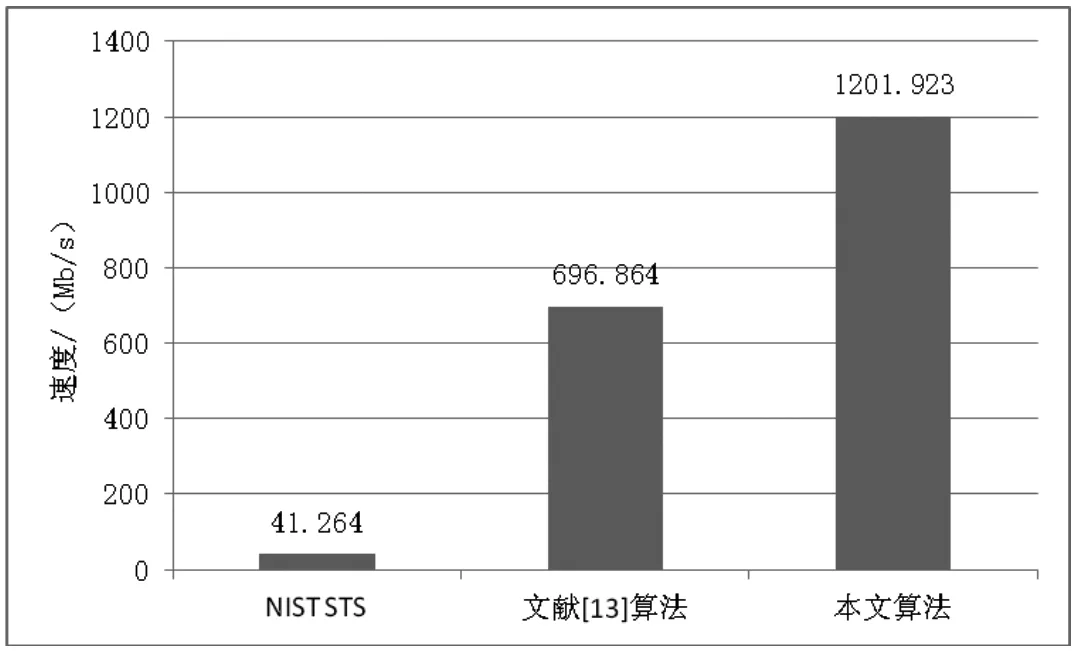
图2 优化前后的算法执行效率

三种Maurer通用统计检测的检测速度对比值，如表4所示。

表4 优化前后的执行效率对比

从统计数据可以看出，Maurer通用统计检测的执行效率有了明显改善。文献[13]算法检测速度是NIST STS检测速度的16.888倍，而本文算法检测速度为NIST STS的速度的29.127倍。可见，本文算法检测速度比文献[13]算法检测速度提升了72.5%。

5 结 语

本文对我国随机性检测规范和NIST随机性检测规范都采用的Maurer通用统计检测算法进行了优化实现，通过对整个宏块做一次性加载处理、减少对数计算等方法，优化改进检测算法。实验结果表明，Maurer通用统计检测的执行效率明显改善，本文算法检测速度为NIST STS的速度的29.127倍，同时比文献[13]算法检测速度提升了72.5%。NIST和我国的随机性检测规范还有很多检测项，其中大部分都还有优化提升的空间，将是今后工作的一个研究方向。