一种对WSN数据估计的改进方法研究*

杨 明，杜 薇，何 军

（1.解放军91404部队，河北 秦皇岛 066001；2.中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引 言

无线传感器网络（Wireless Sensor Networks，WSN）是一种由众多传感器节点构成的自组织网络系统。典型的WSN系统以微型传感器为基础，具备体积小、动态性、分布规模较大和高密度节点等特点，可采取多种方式实现对数据采集、信号监测、协同处理等功能。因此，传感器网络在2000年被美国国防部列为其主要建设领域，并被相关研究机构预测为改变世界的十大技术之一。美军早在20世纪70年代由国防部DARPA发起对传感器网络的研究，代表性的应用有全军军事信息处理系统（C4KISR系统）、海军水下传感器通信网络Seaweb系统和供航母战斗群使用的CEC协同网络系统等。除了国防军事领域，WSN技术在当今已广泛运用于工业控制、环境监测和智能交通等方面。采用大量无线传感器对目标参数数据进行估计，是WSN系统的一个重要作用，也是其能够完成网络监测处理功能的核心步骤，即通过分析处理信号数据，为决策提供必要的支持，得到目标状态参数信息[1]。当前，WSN的估计问题引起了国内外许多研究机构和学者的关注。

在目标WSN系统中，需要对多个节点对应传输的期望信号实现估计。传统的方法是通过寻求期望信号的线性最小均方误差（LMMSE）和传感器信号的线性滤波输出，实现对期望信号的估计。但是，为了满足LMMSE方法的估计性能，节点还需采集大量WSN系统中其他节点发送的传感器信号数据。同时，为了实现最优估计，所有节点都需要交互处理数据，甚至须配置中继节点，导致占用了大量网络带宽，也增加了远距离传输过程中的能量耗损[2]。文献[3]中，研究人员采取了基于奇异值分解（SVD）的估计方法，但算法较为复杂且没有充分提取数据特征，仅适用于一些理论场景。

针对上述问题，本文提出了一种基于树状拓扑的自适应分布式估计方法，可实现对传统思路在估计性能和耗能方面的改进。改进算法中，将各节点接收信号的特征进行融合，提高了鲁棒性；通过进一步优化，节省了节点传输带宽，且树状拓扑结构可以使节点之间的数据传输更加便捷，节省了能量。为了扩展其通用性，各节点之间的信号数据流经合并传送流程后，将被等效为来自根节点的单路信号，其传输过程中的耗能也随之被大部分转移到根节点，从而降低了非根节点的能量损失，也能适用于对异构型传感器网络的状态估计。此外，改进方法还灵活利用了网络汇聚节点的通联关系进行参数交互，达到了减小输入-输出延迟的效果，保证了对待测信号数据估计处理的高效性，并得到了理想的估计效果。

1 信号数据模型

设无线传感器网络WSN系统由K个节点组成，相邻节点之间存在着完备的双向链路，且节点k的邻节点集合即可与其相互通信的节点集表示为Nk。节点k接收到信道Mk中的信号，用yk表示，对应于经过第m个信道发送至节点k处的传感器信号：

其中t表示时间的离散取值，xk,m[t]表示期望信号，nk,m[t]表示加性高斯白噪声。为了说明方便，接收信号可认为是复信号，且可以从频域角度开展描述。需要说明的是，时间的离散取值表示形式在后面的分析中可省略。

在WSN系统中，各节点传感器接收的期望信号分量xk=[xk,1,…,xk,Mk]T由Q个源信号的线性组合表示。它可用叠加在第Q个信道的信号s和一个Mk×Q阶的方向矩阵Ak（Q≤Mk）得到，即：

式中，∀k∈K存在Ak。

系统中，各节点的目标是估计出本地传感器信号的本地期望信号xk。不失一般性，可认为每个节点k对应估计得到的是xk1中前Q个信号，然后定义第Q个信道中信号为=s ，其中为矩阵Ak的一个Q×Q阶子矩阵，含有Ak的前Q行。在集中式网络应用中，所有节点都能接收到各传感器的信号，且节点k通过传感器接收信号y的线性估计器，从而成功实现对的估计[4]，其中H表示共轭转置，且有

节点k可利用LMMSE算法得到Wk估计结果，表达式为：

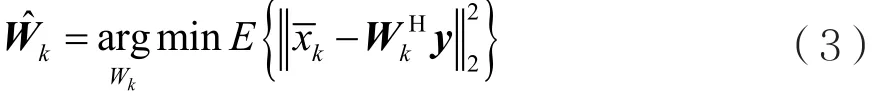
其中，Ryy=E{yyH}，Rxx=E{xxH}。EK是一个M×Q阶矩阵，它的各列都具有等于1的元素，对应于各传感器信号期望，且在其他位置处的元素都为0。根据式（2）以及特定节点期望信号与各节点的最优滤波器输出之间的关系，可推出关系式：

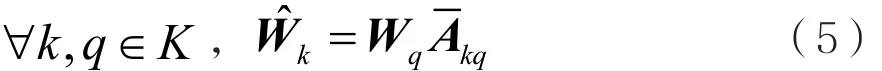
2 改进方法分析

采用基于树状拓扑的自适应分布式估计方法进行改进，将各节点传感器信号与相邻节点接收的信号实现融合。

设节点k采集到自身传感器信号为yk，并接收到来自邻近节点的第Q个信道中融合后信号zqk（q ∈ Nk），其中下标qk表示从节点q发送至节点k的信号。zqk的邻近节点（q∈ Nk）接收信号被表示为堆叠向量的形式，即zk−k。其中，下标-k表示不存在可以获取自身传感器信号的节点zqk。节点k将自身传感器信号与来自其他节点的接收信号一起置为堆叠向量，。期望信号分量也能够用类似的形式表示为x~k。

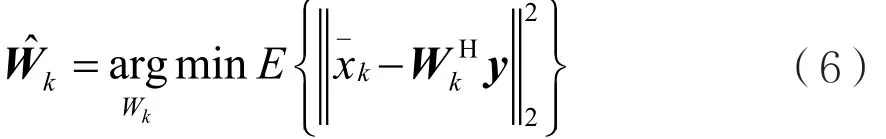
其中i表示迭代因子，并且采取优化生成传输信号参数的融合准则达到更新的目的。特定节点估计量由两个分量组成：用于节点传感器信号Wkk和用于接收信号、。

式（6）还可以用多通道维纳滤波器的形式给出，表达式如下：

通过第i次迭代，节点k的估计信号为：

为了使参数信息高效通过WSN系统，定义了两种类型数据流：一种是从叶节点发送的融合型数据流，向内传播到预定义的根节点；另一种是扩散型数据流，其由根节点发起，当根节点接收到所有相邻节点信号后，再向外传播到叶节点。

（1）融合型数据流

当新的叶节点处传感器信号可观测时，融合数据流进行初始化，将传感器信号的线性组合传送到其中一个邻近节点，即：

然后，将处理结果转发给其中的单节点q，此时未接收到任何信号，即靠近根节点的邻近节点信号。其中，Gku表示Gk-k中的分量，对应于来自邻近节点u的信号 ukz。整个融合过程一直持续到数据流到达根节点为止。

（2）扩散型数据流

当根节点接收到来自其所有相邻节点的信号时，开始发送扩散型数据流。然后，根节点将在本地广播其自身传感器信号和来自邻节点的信号合并数据，即：

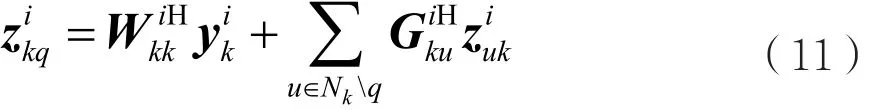
该过程最后将在叶节点终止。

（3）接收机反馈抵消

在扩散型数据流中，当节点发送其本身的传感器信号与所有相邻节点的信号进行融合时，节点k将收到包含有对应于其自身发送信号的一个分量信号。该类型数据流可能会生成一个反馈回路，阻止节点收敛到其最优的LMMSE估计量。但是，这种反馈信号能够采取接收反馈抵消的方法进行去除。

在接收机反馈抵消节点中，可以接入融合型数据流Gqk的Gq-q部分。它可使节点有效消除接收信号中的自身分量。节点k接收到来自邻近节点的融合型数据流的自身信号Gqk，计算表达式为：

此时，需要参数的附加数据流，使得更新速率慢于融合速率和扩散速率。上述情况体现在数据处理流程中。

可定义路径为Pp1→p2，由一组有序节点组成。在图1（a）中，从节点1到节点6，其路径是 P1→6={1,8,2,7,4,6}。同时，可定义 Gp1→p2，遵循之前路径Pp1→p2，使用原来实例，对应于G1→6=G18G82G27G74G46。

图1 新旧两种不同算法中数据流处理流程

图1 （b）中的实线箭头表示融合型数据流，其与传统的估计器公式等价；图1（b）中的虚线箭头表示从根节点到WSN中所有其他节点的广播信号流[5]。

因此，改进方法还可视为式（4）的另一种参数化形式，在节点k处，相应的可得出如下式：

式（13）给出了式（4）最优估计器的解空间，通过设置Gkp=q，对 k 和 q 有 Gk→q=kq。同理，对于全部的k、q和n，有kq=nqkn。然后，根据式（13），得出参数化的，k=1,2,…,K。

可以看出，如果每个节点从根节点接收信号，仍需要消除自身信号。此外，可得出每个非叶节点和非根节点的信号需传输两种类型信号数据流，即扩散型数据流和融合型数据流，以及用于融合型数据流特定节点估计器的部分数据流Gkp。为了减少各节点的传输负担，希望去除扩散型信号数据流，并允许根节点将单个信号传播到所有其他节点。此时，可假设根节点具有较大的能量估计[6]。图1（b）中给出了一个采用改进方法处理数据流的例子。当每个节点从根节点接收信号时，可采用基于树状拓扑的自适应分布式估计方法，实现相邻节点和其他各节点的相互数据传输得到最优估计量。不妨可假设节点r是树的根节点，并定义从根节点到节点k的路径为Pr→k。在扩散型数据流中，每个节点将接收到在根节点处的广播信号，且Gr→k来自于根节点，可视为所有的Gmn节点（n∈Nm，m,n∈Pr→k）与根节点的积。然后，节点k收到来自于根节点的信号。与用于根节点处广播信号的Gr→k相同，它的计算表达式如下：

为了验证改进方法的有效性，进行了下面的仿真实验。

仿真一。设目标WSN系统由20个节点组成，WSN中传感器信号数据的采样率为200 MHz，信号数据采样点长度为1 024，数据率为640 kb/s，每个样本所处的环境尺寸为5 m×5 m，且每个期望源信号随机分布在环境中，均匀分布区间为[-0.5，0.5]。对传统的WSN估计方法和改进方法进行对比，仿真结果如图2所示，其中横轴表示估计算法的迭代次数，纵轴表示估计中的最小二乘代价。

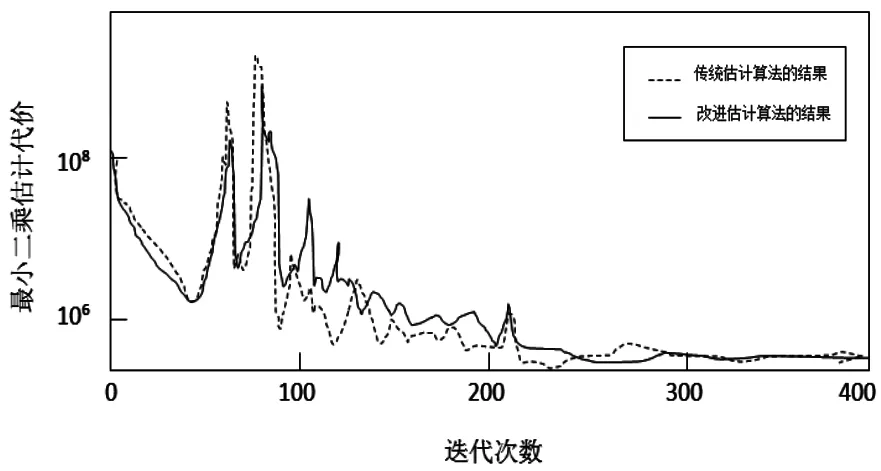
图2 采用不同估计方法得到的代价结果

从图2还可以看出，改进方法比原来的估计方法具有更快的收敛速度。

仿真二。下面对不同估计方法的能耗进行仿真分析，仿真条件同前所述，设期望源信号与传感器噪声之间不相关，结果如图3所示，其中横轴表示不同的估计方法，纵轴表示能耗。该仿真试验是基于根节点与非根节点各自耗费的平均能量结果进行的。

图3 采用不同估计方法的能耗分析

从图3可以看出，利用改进方法中的广播策略，可以使非根节点耗费的平均能量减少。综上所述，相比采用传统的估计方法，改进估计方法的性能更优。

3 结 语

本文对大规模无线传感器网络WSN系统中的数据估计问题进行了研究分析，提出了一种改进的估计方法，能够减少系统的整体输入-输出延迟，并将能量使用率转换为根节点的能量消耗。在这种改进方法中，节点具有较强的广播能力。同时，经过优化计算，新方法节省了估计处理所需的能耗，且树状拓扑结构便于数据融合过程中的交互，更进一步减小了数据带宽。通过仿真测试，验证了改进方法的结果正确性。改进方法工程实用性强，今后还将进一步探索，以增强其在复杂环境中的性能。