基于临界面-损伤参量法的高压涡轮盘多轴疲劳寿命预测

徐燊，朱顺鹏，郝永振，廖鼎

电子科技大学 机械与电气工程学院 系统可靠性与安全性研究中心，成都 611731

高压涡轮(HPT)盘作为航空发动机关键部件之一，其正常地工作运转对航空发动机的结构完整性与可靠性具有重要意义。通常，高压涡轮叶盘工作环境恶劣，受到高转速、高温以及异常振动等复杂载荷的影响。涡轮部件的损伤机制常包括多轴疲劳(包括高周疲劳和低周疲劳)、蠕变断裂、高温腐蚀及其间交互作用[1-5]。由于气流引起的振动载荷的振幅远小于离心载荷的振幅，因此通常认为振动会导致高周疲劳、离心载荷导致低周疲劳[4-5]。特别是涡轮叶片与涡轮盘相互作用面处的较高接触应力和短周期震荡会导致微动磨损并促使其最终失效。对于涡轮盘的失效机理分析，Kermanpur等[6]指出涡轮叶片与涡轮盘的榫头与榫槽之间的间隙不足会导致裂纹发生并且最终造成涡轮盘整体失效。通过将有限元法计算所得的接触应力和体积应力作为寿命评估分析的输入，Golden和Calcaterra[7]提出了一种用于分析枞树型微动疲劳的裂纹扩展寿命预测模型。Chen等[8]基于低周疲劳和蠕变疲劳相互作用下的应力应变响应，采用修正的线性损伤累积法和修正的应变程分割法对涡轮盘榫槽区域进行了寿命预测，但忽略了枞树型区域的高接触应力和缺口的影响。考虑到发动机服役过程中涡轮叶盘榫连结构不规则曲面致使的多轴应力应变状态，开展涡轮盘榫槽与叶片榫头连接部位的多轴疲劳寿命预测对确保发动机涡轮结构完整性尤为重要。针对此，建立准确的多轴疲劳寿命预测模型是很有必要的。作为多轴疲劳寿命预测的常用方法，临界面法已经被证实能较好地用于复杂应力作用下工程部件的疲劳寿命预测与分析[9-10]。

至今为止，国内外学者已提出多种临界面寿命预测模型，包括Fatemi-Socie (FS)[11]、Wang-Brown (WB)[12-13]和SWT(Smith-Watson-Topper)[14]模型。最初Brown等[15]提出了一个以最大剪切应变平面作为临界面的寿命预测模型，该模型考虑了临界面的剪切应变和法向应变但并没有考虑平均应力效应的影响。基于此，Wang和Brown[12-13]对其进行了平均应力修正，但忽略了循环硬化效应对寿命的影响。针对此，Fatemi和Socie[11]提出了用临界面的法向应力来代替法向应变，较好地预测了存在平均应力和循环硬化影响的材料的多轴疲劳寿命。Smith、Watson和Topper[14]指出疲劳失效主要是由最大主应变所垂直的平面的裂纹扩展造成的。对于拉伸裂纹失效模式，SWT模型具有较好的寿命预测效果，但对于纯扭转和多轴疲劳，其预测效果较差[16-18]。Jiang和Sehitoglu[19]对SWT参量进行了修正，通过拟合材料常数能对不同的裂纹行为作出合理的预测。文献[20-22]研究表明，在实际工程应用中应该考虑平均应力对寿命的影响。吴志荣等[23]以最大剪应变幅作为主要损伤控制参数，以最大剪应变幅平面上的SWT参量作为多轴疲劳第二损伤控制参数，提出了一个新的多轴疲劳模型。李静等[24]将多轴疲劳模型应用到缺口试件，并分析了平均应力对疲劳寿命的影响。Ince和Glinka[25]以疲劳参量的最大值作为临界面，基于广义应变能建立了多轴疲劳损伤参量的2种不同形式。

本文根据临界面的应力应变曲线的研究，同时考虑最大剪切平面上的正应力和正应变，基于FS损伤参量提出了一个新的多轴疲劳临界面-损伤参量，同时对当前常用临界平面模型进行了对比和评估。最后结合某高压涡轮盘的寿命预测，进行了模型对比与分析。

1 临界面多轴疲劳模型

1.1 FS 模型

Fatemi和Socie[11]针对剪切失效模式建立了一个多轴疲劳寿命模型，该模型的损伤参量考虑了裂纹初始及其扩展，因为这个参量包括剪切应变幅和临界面最大法向应力，并认为剪切应变是导致初始裂纹的原因，而最大法向应力能够促使临界面裂纹的扩展，该模型为

(1)

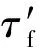
1.2 SWT模型

SWT模型最初的提出是为了解释单轴载荷下平均应力对寿命的影响，且该模型也能用于由拉伸裂纹失效主导的多轴疲劳寿命预测[14]。SWT参量包括了最大主应变幅和最大主应变所垂直平面上的最大法向应力，其表达式为

(2)

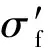
2 新的多轴疲劳临界面-损伤参量模型

在基于临界面法的结构多轴疲劳寿命预测中，根据疲劳裂纹不同的失效模式，往往会选取不同的临界平面。针对剪切失效模式，临界平面一般选取最大剪切平面，如FS模型；而对于拉伸裂纹主导的失效模式，则一般会选取最大拉伸平面作为临界平面，如SWT模型。最近，也有学者以最大损伤平面作为多轴疲劳损伤分析的临界平面[26]。由于本文中GH4169合金疲劳裂纹失效模式属于剪切失效型[1]，故采用SWT模型进行多轴疲劳寿命预测时精度较差，但是采用剪切失效型的FS模型进行多轴寿命预测时，预测效果明显偏于保守。

一般认为，疲劳裂纹的萌生是由材料内部稳定滑移带的局部塑性变形所致，而裂纹面往往为最大剪应变幅平面[27]，因此，常以最大剪应变幅作为裂纹萌生的主要控制参数，而最大剪应变幅平面上的正应变和正应力会加剧疲劳裂纹的扩展，故应将它们都作为疲劳损伤的辅助控制参数。而FS模型则仅考虑临界面上正应力对疲劳损伤的影响，这也是FS模型被认为对GH4169材料预测偏于保守的原因。

通过上述分析，针对GH4169合金比例和非比例载荷下的多轴疲劳问题，本文基于FS模型提出以最大剪应变幅γa为主要损伤控制参数，以最大剪应变幅平面上的正应力和正应变组成的修正参数作为多轴疲劳损伤的第二控制参数，提出如下多轴疲劳临界面-损伤参量(MFS模型)即

(3)

式中：DP为损伤参量；Δεn为最大剪应变幅平面上的正应变变程；β为单轴拉压疲劳修正参数，其物理意义是将单轴疲劳数据修正到纯扭转疲劳数据的水平，是由拟合单轴拉压试验数据得到，估算方法如下所述。

对于单轴拉压疲劳有

(4)

(5)

(6)

(7)

式中：υ为泊松比；υe为弹性泊松比；υp为塑性泊松比。

将式(4)～式(7)代入到式(3)即可得参数的计算公式为

β=

(8)

3 模型验证

3.1 GH4169材料模型验证

为评估上述2种临界法寿命预测模型并验证所提出的多轴疲劳临界面-损伤参量模型，选用文献[28-29]中轮盘合金GH4169在650 ℃下的单轴与多轴疲劳试验数据。单轴疲劳试验是在应变比R=-1的拉压载荷下进行，而多轴疲劳试验是在0°比例、45°和90°非比例拉扭循环载荷下进行的。GH4169的单轴疲劳常数如表1所示。在有限试验数据的情况下，纯扭转疲劳材料常数可通过单轴疲劳材料常数换算而来，根据文献[30]，模型参数有如下近似关系：

(9)

基于单轴疲劳数据分别拟合出FS模型和MFS模型中的材料常数k=0.47和β=0.5。为真实反映循环加载的情况，在有限元仿真中耦合了Chacoche本构模型[31]，该模型所设置的屈服应力为基于0.05%塑性应变计算而来。如图1所示，SWT模型和FS模型对单轴疲劳寿命具有较好的预测能力，但是SWT模型对多轴疲劳寿命预测明显偏于危险，而FS模型对多轴疲劳寿命预测又偏于保守。如图2所示，新提出的MFS模型虽然单轴疲劳寿命预测能力略低于前两者(预测寿命也大多数在2倍误差分散带以内)，但在多轴疲劳载荷下的寿命预测能力得到较大提升。由图3中模型预测误差对比可知，MFS模型对于多轴疲劳寿命预测的能力最好。

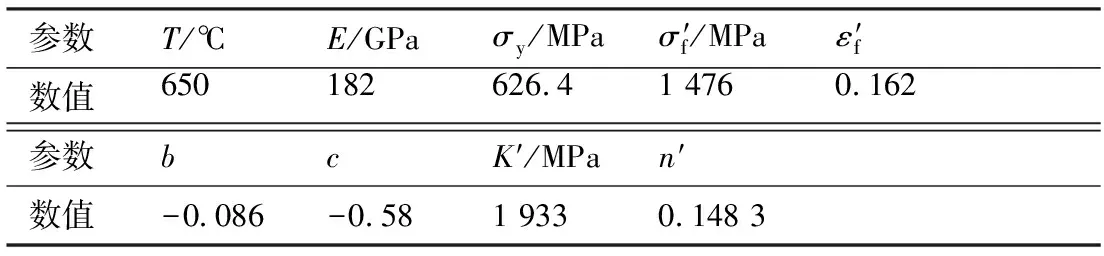
表1 GH4169的材料常数Table 1 Material properties of GH4169

3.2 涡轮盘寿命预测

针对某高压涡轮叶盘在装配情形下进行有限元仿真计算，其中涡轮盘材料为GH4169合金，涡轮叶片材料为K403合金，2种材料的单轴疲劳常数分别如表1和表2所示。仿真条件为650 ℃常高温与离心载荷，同时对叶片榫头与轮盘榫槽进行接触分析，并计算输出叶盘榫连结构处的多轴应力应变状态。涡轮叶片与涡轮盘的网格划分如图4(a)所示，榫头采用20节点六面体单元，叶身采用10节点四面体单元。榫头与榫槽的接触部分使用的是面面接触单元。为了获取榫连结构区域更准确的应力应变状态，对其进行了恰当的精细化处理。该涡轮盘的载荷谱根据其真实飞行任务包括3种典型循环，如表3所示。

涡轮盘在起动—最大—起动的循环转速加载下的有限元仿真结果如图4所示。分析发现涡轮盘的临界最危险区域在榫槽部位，这与Sinclair和Cormier[32]中结论类似。由于榫连结构在高温情形下的膨胀和受到过高的离心载荷，导致榫槽的第一个隼齿处产生塑性应变，且由图4中可知最大等效塑性应变和最大等效应力的位置不一样。值得一提的是，基于上述结果，运用式(3)可进一步计算获得MFS最大损伤参量分布，并确定出最大损伤参量的位置，并由此计算轮盘寿命；结果显示，最大等效应力的位置并不是部件寿命最低的位置，该结论与Maktouf等[33]研究结论吻合。

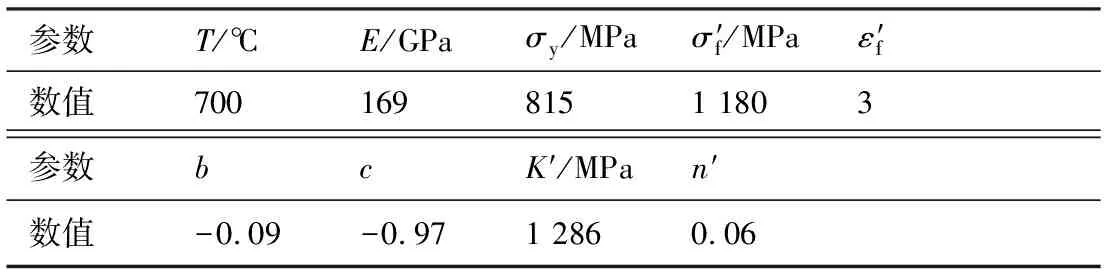
表2 K403的材料常数Table 2 Material properties of K403

模型预测寿命起动—最大—起动(0-450 r/s-0)慢车—最大—慢车(230 r/s-450 r/s-230 r/s)巡航—最大—巡航(431 r/s-450 r/s-431 r/s)SWT4.395×1049.290×104>1×1012FS3.985×1052.194×106>1×1012WB7.231×1049.979×104>1×1012Proposed (MFS)4.807×1053.324×106>1×1012

表3中，列出了该涡轮盘在典型工况循环下不同模型所预测的寿命，可知在起动—最大—起动和慢车—最大—慢车的工作状态下，对比该涡轮盘现场使用寿命，WB模型与SWT模型所预测的寿命较为一致，略偏保守，而FS模型和MFS模型所预测的寿命较高，这是由于MFS模型中的材料常数β随着寿命的增加而增大所导致的。此外，对比该涡轮盘现场使用寿命，在起动—最大—起动的工作状态下，若简化并直接采用轮盘结构中单轴最大等效应力进行计算，结合文献[29]中轮盘合金S-N曲线，预测轮盘寿命约为1 548次循环，明显过于保守；对照该涡轮盘在考虑疲劳寿命分散系数修正后的设计寿命(约为8.1×104次循环)，本文新提出的临界面-损伤参量模型及SWT、WB、FS等多轴疲劳模型较单轴疲劳模型更准确地预测了其在不同工况下的疲劳寿命。

4 结 论

1) 针对基于FS损伤参量的多轴疲劳寿命预测较为保守的现象，通过引入最大剪应变幅平面上的正应力和正应变损伤参量，提出了一个新的临界面多轴疲劳损伤参量模型。

2) SWT模型能较好地预测高温合金GH4169的单轴疲劳，而对多轴疲劳其预测能力不足；FS模型能较好地预测单轴、多轴比例与非比例加载下的疲劳寿命，但是对多轴疲劳寿命预测略显保守。结果显示，本文所提出的新的临界面-损伤参量法能较准确地预测多轴疲劳寿命。

3) 结合某高压涡轮盘在典型工况下寿命分析发现，榫槽是其失效的关键部位，通过确定轮盘结构的最大损伤参量位置，进而计算其寿命；结果显示，最大损伤并没有发生在最大等效应力最大的区域。