机器学习技术在织机运行状况预测中的应用

侯 涛

为了确保经编机在生产中维持正常运转,可以通过经编机的历史运行数据、实时运行数据和已经设置的织机运行参数来预测织机的运行状况。传统的预测分析是在历史资料基础上得到客观规律,结合相关领域专家的专业经验,预先对各种可能发生的运行状态先验地预测其概率。但是先验分布具有一定的局限性,先验分布和许多决策问题的准确性易受到先验信息充分与否的影响,同时决策人预先对状态可能发生的概率做出的主观判断与客观真实情况存在一定的差距。

近年来人工智能技术发展迅速,为提高纺织机械设备故障预测技术的可靠性和有效性,将人工智能相关技术引入到纺织机械设备故障预测中来很有必要。本文通过分析经编机故障的性质、分类与影响经编机故障预测的各类指标,构建了经编机故障预测框架;通过使用主成分分析法对影响经编织机故障预测的各类指标降维处理,构建了基于距离判别法的经编织机故障预测模型,从而实现了经编织机的故障预测。

1 经编机运行故障预测的理论基础

1.1 经编机故障影响因素分析

对影响经编机故障预测指标进行分析,以获得反应经编机生产状态的特征量,从而采用基于主成分分析和距离判别法理论进行经编机故障预测模型的建立。在对纺织厂进行了实地调查基础上,通过对经编机生产运行过程的分析,对经编机故障预测指标的建立从离散型数据和连续性数据两方面入手,其结构如图1所示。

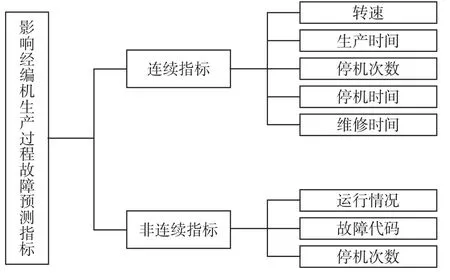
图1 影响经编机故障预测指标体系

经编机的故障是一个从正常状态到故障的逐步演化的多状态过程,将经编机运行状态分为正常、停机、换盘、故障、维修。在停机状态下不可能向故障状态转变,当经编机发生故障时运行状态从正常状态向故障状态转变,当经编机换盘后品种不合适可能会造成经编机故障。

1.2 主成分分析

主成分分析(PCA)是一种较为成熟的多元统计监测方法。应用PCA的方法将显式变量作一定的线性转化产生数量较少的隐式变量,降低原始数据空间的维数,再从新的隐式变量中提取主要变化信息及特征[1]。这样既保留了原有数据信息的特征,又消除了变量间的关联、简化分析复杂度;从新的数据空间中提取符合相应要求的主元数,同时也消除了部分的系统噪声干扰。特征或属性太多会增加问题的复杂程度与难度,主成分分析就是把原来多个特征化为少数几个特征指标的一种统计分析方法,从数学角度看这是一种降维处理[2]。

为了消除量纲的影响,将变量标准化后再计算其协方差矩阵。任何随机变量对其作标准化变化之后,其协方差与其相关系数是一回事,即标准化后的变量协方差矩阵就是其相关系数矩阵。根据协方差的公式可以推得标准化后的协方差就是原变量的相关系数,即标准化后的变量的协方差矩阵就是原变量的相关系数矩阵。也就是说,在标准化前后变量的相关系数矩阵不变。

主成分分析的计算步骤如下：

(1)将变量进行标准化处理;

(2)计算相关系数矩阵;

(3)求出相关系数矩阵的特征值及相应的正交化单位特征向量;

(4)选择主成分;

(5)计算主成分得分。

1.3 距离判别分析

距离判别法的基本思想是根据已分类的样本空间的样本数据,计算出每个分类的重心即分类均值。若待检样本与某类的重心距离最近,就认为它是来自于该类。距离判定方式有欧氏距离、曼哈顿距离、切比雪夫距离及马氏距离等。

马氏距离的计算与原始数据测量单位没有关系,不受指标单位不统一的影响,故本文选取马氏距离作为距离度量公式。马氏距离能够有效计算两个未知样本集的相似度,表示协方差的距离。其物理意义就是在规范化的主成分空间中的欧式距离,即首先利用主成分分析将样本分布改变到另一个空间,而马氏距离就是样本在新空间中分布的欧氏距离。

2 经编机故障预测运行过程

2.1 经编机故障预测框架

图2所示为基于PCA与距离判别法的经编机故障预测框架,对历史样本进行主元分析,确定模型的主元及提取经编机故障特征信息形成模型的训练集,并由此得到主成分分析-距离判别法经编机故障预测模型[3]。对经编机实时采集的数据进行相应的预处理,得到经编机实时数据的特征信息,并将其输入预测模型中完成经编机故障预测。

使用主成分分析与距离判别法进行经编机故障预测的基本流程见图3,整个流程图由三部分组成,即经编机故障预测模型的建立与利用经编机故障预测模型进行故障预测,其中数据预处理包括数据的整理和数据标准化处理两部分。

图2 经编机故障预测模型

图3 经编机故障预测的基本流程图

2.2 经编机故障预测模型

2.2.1 数据预处理

本文结合本领域专家的知识和经编机生产历史数据统计表,选取影响经编机故障预测指标中的8个特征参数作为条件属性,分别为转速、经编机运行情况、故障代码、生产时间、停机次数、停机时间、维修次数、维修时间;采取经编机运行8个特征参数作为判别依据,对各属性值按连续数据和离散数据进行如下划分：

(1)连续数据 主要包括转速、生产时间、停机时间、维修时间,这些连续数据都属于连续值。为了更好地利用主成分分析理论对经编机故障预测指标进行降维处理,必须对样本空间中存在缺失值的样本点进行缺失值插入处理。为保持样本空间原有的分布,本文采用的是均值插入方法。

(2)离散数据 主要包括经编机运行情况、故障代码、停机次数等。对离散数据进行缺失值处理时依然采用的是均值插入方法,但缺失值的替补值不再是平均值,而是用该样本点所在的样本空间中其他所有样本点存在值的众数来代替该缺失值。

2.2.2 主成分分析

主成分分析是经编机故障预测模型中不可或缺的模型,因为在原始数据集中属性与属性之间可能存在相互关系,而这种相互关系会造成模型的预测效果不好,可能会产生过拟合现象。本文采用主成分分析进行降维处理,其基本计算方法是：将训练样本集进行标准化处理,计算样本空间样本点的相关系数矩阵,求出相关系数矩阵的特征值及相应的特征向量,然后计算主成分贡献率及累计贡献率,再计算主成分载荷,最后计算因子判别式[4]。

算法步骤如下：

(1)根据主成分分析原理将数据进行标准化处理;

(2)根据算式求相关系数矩阵,并计算相关系数矩阵;

(3)选取主成分特征值越大相对应的主成分数据越重要,选取主成分数据一般包含到85%以上即可,代表标量的大部分原始信息[5];

(4)计算主成分载荷,它主要反映主成分与原变量的相互关联程度;

(5)根据主成分载荷矩阵,计算因子判别式;

(6)输出因子判别式。

2.2.3 距离判别法模型的建立

采用马氏距离其基本方法是：首先计算各类样本空间的均值,然后计算各个样本空间的协方差矩阵,计算任意两样本空间的距离,求出线性判别函数,实现预测功能。

算法步骤如下：

(1)根据距离判别法计算样本均值;

(2)计算样本的协方差矩阵;

(3)计算任意两总体距离;

(4)根据计算的总体距离,得出线性判别公式。

2.2.4 故障预测模型验证

预测模型验证实质上就是进行模型有效性分析,是判断建立的预测模型是否准确代表实际系统;一方面是确保采集的数据适用于建立的预测模型,另一方面是检验模型输出是否接近实际系统。判别结果的评价一般根据对原始数据、验证样本的准确预测来评价分类效果的好坏,对原样本及训练样本验证方法有组内考核,组内回代,对验证样本的验证法有组外考核等。

本文所采用的验证方法如下：

(1)对于训练样本,采用组内回代法验证模型效果是否准确,假设G1,G2…Gn为n个总体,分别抽取容量为n1,n2的样品,设nmn表示实际归类Gn,预测归类Gm的样本数。使用误差率来估计误判率,准确率为1减估计误判率,其算式为：

(2)对于验证样本,将验证样品代入预测模型,与实际结果进行比较。

3 结语

通过分析影响经编机故障预测的各类指标,采用基于主成成分分析对海量的经编机生产状态数据进行降维处理,并构建了基于距离判别法评估的故障预测模型,从而实现了经编机的智能化故障预测。通过测试数据集进行验证,结果显示预测误判率较低。