低质量比舵系统流致振动特征研究
2018-09-28王人凤尤云祥胡晓峰
王人凤, 尤云祥, 陈 科, 胡晓峰
(上海交通大学 海洋工程国家重点实验室 高新船舶与深海开发装备协同创新中心,上海 200240)
颤振是一种由弹性力、惯性力、阻尼力和流体自激力共同作用引起的弹性不稳定现象。由于这类振动有可能演化为发散振动,故该现象一旦发生,结构就存在损坏的风险。经典颤振理论认为质量比(μ=m/πρb2l,m为系统质量,ρ为流体密度,b为舵的半弦长,l为舵的展长)低于临界质量比时颤振便不会发生,但一些试验表明,当水下升力体的质量比较小时也有可能发生颤振[1]。颤振理论最初应用于航空领域,后又被推广到船舶领域。机翼的临界颤振速度随着机翼质量、质心到刚心的距离以及结构阻尼系数的增加而增大。当结构具有立方非线性刚度时,系统会在一定的速度范围内做稳定的极限环运动,并且极限环的幅值会随着流速的增加而增大。但是,当流速增大到一定程度时,系统进行发散振动。在求解振动方程时,不同的初始积分条件也会对系统极限环振动的幅值产生影响[2]。
张琪昌等[3]针对含立方非线性刚度二元机翼系统颤振时的极限环振动开展了相关研究,对分岔点类别和平衡点的性质进行了定性的分析,进而研究了系统参数尤其是机翼外形变化对极限环颤振稳定性和幅值的影响。发现当平衡点为稳定的焦点时,机翼会进行衰减振动,满足设计要求。但是,在平衡点的附近也有可能出现稳定的极限环颤振运动,甚至是不稳定的极限环颤振运动。在工程上,对于小振幅稳定极限环颤振,只要不引起疲劳破坏就可以满足要求;而对于不稳定的极限环颤振运动,必须避免。设计中可以通过改变系统的参数来抑制振幅和临界颤振速度的大小,从而避免不稳定极限环颤振运动的产生。赵海等[4-5]求解某弹性系统的颤振速度并进行了数值验证,分析了系统各参数对颤振速度的影响,并讨论了非线性刚度系数对系统沉浮和俯仰自由度颤振极限环幅值的影响。结果表明,忽略非线性阻尼项会对超声速流二元机翼的颤振计算造成误差。其研究还显示,虽然系统运动微分方程具有对称性,但两个自由度上的结构参数对系统临界颤振速度的影响却不具有对称性。张瑜等[6-7]利用变步长四阶龙格库塔法对二元机翼系统的运动微分方程进行数值模拟,对不同流速区间内平衡点、极限环个数以及稳定性进行研究。同时还对极限环分叉问题进行了数值模拟,结果表明系统的极限环也有可能产生和平衡点一样的分岔现象,且随着无量纲流速的增大,极限环振动会经过倍周期分叉转化为混沌运动。
Hamdani等[8-9]将有限元方法应用于翼型的动力特性分析中,一方面可以得到翼型表面的压力分布,另一方面也可以得到翼型附近的流体分布。翼型在低雷诺数下同样会出现运动速度突然增大或减小的情况,并且在此期间会产生一个较大的升力,导致翼形的进行明显的沉浮和俯仰运动。在这种不稳定的运动发生期间,会在翼型的上下表面不断出现一层层范围更大的漩涡。Münch等[10]利用CFX模拟了NACA0009翼型在湍流中的动力特性。翼型的初始攻角为2°,流速为5~15 m/s,计算结果与实验数据吻合,误差小于2%。Gnesin等[11]利用一种考虑旋转叶片振动因素的三维流固耦合求解方法研究了涡轮转子的振动问题。发现在叶片振动的幅值-频率谱上存在高频和低频,但是这些频率并不是转子的倍频。Amiralaei等[12]为分析NACA0012翼型在低雷诺数流体中的振动特性,分别选取攻角2°~10°,使用有限体积法求解Navier-Stokes方程,并将计算结果中的瞬时升力系数与利用Theodorsen理论求解的结果进行比较,发现雷诺数不仅对翼型的升阻力系数有影响,对翼型的振动特征也存在明显的影响。Akcabay等[13]利用CFX求解非定常雷诺平均Navier-Stokes方程分析空泡对NACA66水翼水弹性稳定性的影响。随着空泡量的增加,翼型的平均升力随之减小而平均阻力增大,同时其平均变形幅度也随之减小。此外,由流动引起的振动幅值和阻力随着翼型刚度的减小而增大。刘胡涛等[14]利用流固耦合方法对二元水翼的运动进行数值模拟,分析了初始攻角、刚心位置以及来流速度对水翼振动特性的影响。使用大涡模拟方法计算高雷诺数下水翼绕流场以及流场力作用于两自由度刚体上所导致的周期性沉浮和俯仰运动。采用龙格库塔法求解刚体水翼的运动方程,位移参数作为下一时间步流场计算的边界条件。结果表明,水翼振动状态对系统的初始值具有依赖性,在没有扰动的情况下,水翼在零攻角时始终保持微幅振动。随着初始攻角的增大,振动平衡位置越偏离初始位置,且沉浮运动幅值衰减较明显。来流速度对水翼振动影响较为显著,并且当来流速度增大到一定程度时,水翼会出现颤振现象。此外,还发现水翼颤振产生的条件比较苛刻。尽管如此,随着流速的增大,系统产生的振动加剧现象仍不容忽视。
若舵具有较小展弦比,利用两自由度系统动力方程分析振动特性时需要考虑其三维效应,所以有必要对理论模型进行相应的参数修正。此外,鉴于低质量比(μ<1)舵系统颤振相关研究较少,通过数值模拟方法分析颤振发生时舵周围的流场变化也很有必要。
1 模型和计算方法
1.1 小展弦比两自由度系统动力模型
舵系统由一个截面为NACA0017的舵、一根刚性轴以及与其连接的弹性装置组成,刚性轴与舵固接。其中,舵的展长l=0.39 m,两端弦长不同,舵根侧面(较大的侧面)的弦长为0.3 m,舵稍侧面(较小的侧面)的弦长为0.2 m,则中截面的弦长c=0.25 m。可以将舵系统简化为经典两自由度舵模型,如图1所示。其主要结构参数如表1所示。

图1 有限展长舵的两自由度振动理论计算模型Fig.1 Two-degree-freedom vibration mechanical model for a foil with a finite span
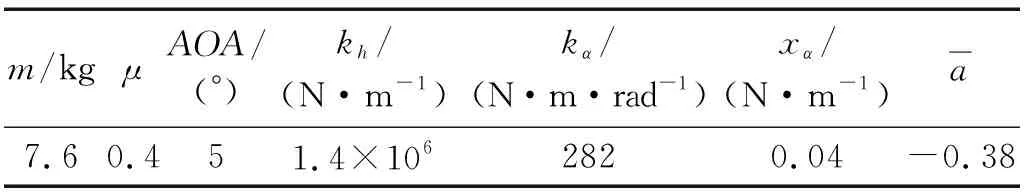
m/kgμAOA/(°)kh/(N·m-1)kα/(N·m·rad-1)xα/(N·m-1)a7.60.451.4×1062820.04-0.38
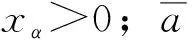
当舵做简谐运动时,会受到升力L(向上为正)和俯仰力矩Tα(迎流抬头为正)的共同作用,并在流体动力的激励下发生两个自由度的运动,一个是舵-轴部件的沉浮运动,位移为h,向下为正;另一个是舵随刚性轴转动而产生的俯仰运动,俯仰角度为α,迎流抬头为正。
(1)
式中:V∞为流速;C(k)为Theodorsen函数; 式中与C(k)无关的项来自惯性效应。
考虑展弦比对结构振动的影响,对该式进行修正。代表惯性效应的项添加附加质量修正系数ε,而环量项添加环量修正系数δ,得到
(2)
其中,
(3)
式中:AR=l/(ccosAOA),AOA为初始攻角;τ为舵的形状参数。
通过Fourier变换和引入Wagner函数[15],结合舵的两自由度任意运动微分方程
(4)
可以得到
(5)
其中,
(6)

将式(5)写为矩阵形式,有

(7)
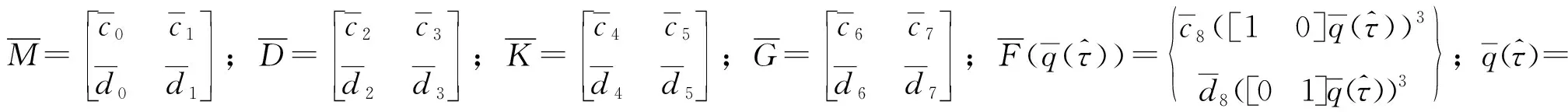

(8)

从而得到两自由度系统任意运动的无量纲动力方程为
(9)
1.2 流体模型
使用CFD(Computational fluid dynamics)商业软件中的弹簧构件生成系统特定的支撑刚度,并利用UDF(User Defined Function)通过添加与俯仰运动方向相反的俯仰力矩来模拟相应的扭转刚度。对于流体域,左侧以及前后壁面为速度入口,上下为固壁面,右侧为压力出口,如图2所示。

图2 数值模拟几何图Fig.2 Geometric model of numerical simulation
当低速航行时,舵系统周围的流体可以视作不可压流体。质量守恒方程和动量守恒方程组成了黏性不可压流体的基本控制方程,而控制方程正是这些守恒定律的数学描述。现实中的湍流流动是一个随机变化的脉动量,由于很难在计算中完全反映这些脉动量,所以引入雷诺时均的概念,将任一流动变量的瞬时值进行分解,并看作平均值和脉动值之和。
三维瞬态不可压流体质量守恒方程为
(10)
时均值的动量守恒方程,即雷诺时均纳维尔—斯托克斯(Reynolds Average Navier-Stokes, RANS)为[16]
(11)
式中: (u,v,w)为流速在直角坐标系中的三个分量;ρ为流体的密度;p为压力;μ为流体的动力黏性系数;g为重力加速度。
由Boussinesq假设,引入湍流动力黏性系数μt,可以得到雷诺应力张量和流体时均速度梯度之间的关系
只要选择合适的湍流模型将μt确定,就可以使RANS封闭。本文选择的SST(Shear Stress Transport)k-ω模型(经剪切应力修正的两方程模型)结合了标准两方程模型k-ω和k-ε的优点,在近壁面区域利用k-ω模型,而在远离附面层的区域使用k-ε模型,可以精确地计算物体表面流体的逆压梯度以得到物体附近流体的细微变化[17-18]。
1.3 流固耦合设置
把舵系统的运动看作是一种刚体运动,其重心位于刚体运动局部坐标系的原点。为了保持和实际情况一致,在刚心的垂向位置添加了弹性系数为kh的弹簧组构件,并通过UDF设置了舵系统绕刚性轴方向的俯仰力矩,其表达式为
Tα=-kαθ
(12)
式中:θ为舵转动的弧度。
舵系统在运动过程中所受到的回复力F和俯仰力矩Tα为
(13)
(14)
式中: [τ]和p为作用的剪应力和压力;r-rc为舵表面任意网格中心到舵重心的距离(用位置矢量表示);n为舵表面的外法线方向。
得到舵系统的受力之后,需要进一步计算其运动姿态。引入舵系统的两自由度运动方程可得
(15)
(16)
式中:v为舵系统沉浮运动的速度;M为惯性矩张量在绕轴方向上的分量;ω为舵系统俯仰运动角速度。由式(15)和式(16)可以求得舵系统运动的速度、角速度以及位移,进而确定其运动姿态。在求解过程中,每个时间步长内对离散方程进行多次迭代,当满足收敛条件时输出速度和角速度等参数,并即时更新网格节点的位置,从而实现舵系统在流体中运动的数值模拟。
1.4 网格划分
在舵和流体耦合的过程中,网格移动是耦合界面数据传递的关键。当结构的运动形态存在较大变化时,网格移动速度和准确度会对数值模拟结果的效率和精度产生巨大影响。重叠网格技术(Overlapping Grid Method,OGM)的使结构网格的自动更新成为可能。OGM将覆盖整个计算域的母网格和运动物体的子网格进行叠加来描述物体间的相对运动,各区域中的计算网格独立生成,流场信息通过插值函数在重叠区边界进行匹配和耦合,从而实现网格的自动更新。
依据舵模型的尺寸建立相应的几何模型,并划分面网格,网格数为23 834个,如图3所示。
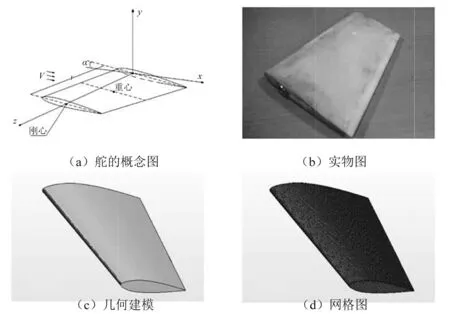
图3 舵的概念、实物、几何建模和网格图Fig.3 Conceptual graph, photograph, geometric model and grid of the hydrofoil
图4为体网格的划分,网格数为122万个。其中,对舵表面附近的网格进行了加密。在计算域内采用动网格技术,舵附近和外边界分别设置了不同的网格密度,舵附近的网格最密,而越接近外边界网格越稀疏。重叠网格实现了不同网格区域的数据传递,而通过设置疏密程度不同的网格,既可以精确反映舵表面附近的流场变化,又可以提高计算速度。
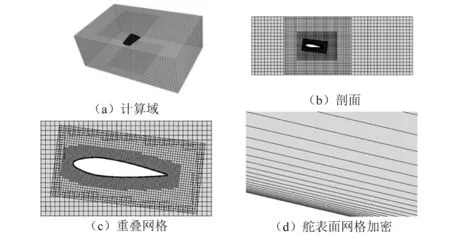
图4 网格划分Fig.4 Mesh generation
2 结果与分析
2.1 振动特性分析
图5为舵系统振动理论值的V-g曲线,在给定的系统参数下存在一个临界航速VF,当V∞
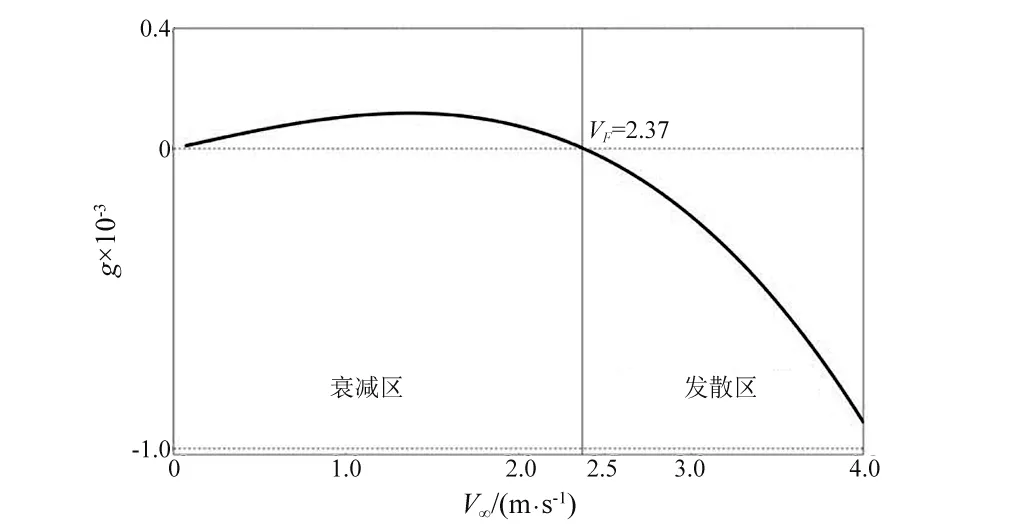
图5 舵系统振动计算值V-g曲线图Fig.5 Computed V-g curve for the vibration of the hydrofoil system
舵系统沉浮和俯仰振动幅度的实验值变化曲线,如图6所示。系统的两种振动成份均随着V∞增加而增大。沉浮振动幅度曲线在V∞=2.37 m/s时出现一个明显的波动,并且此流速所对应的频谱图上在原有频率成份的波峰1附近出现了明显的伴随峰值。可以认定此时系统发生颤振,但是这种颤振与高质量比(μ≫1)系统的颤振不同,其振动V-g曲线向下凸。从实验现象来看,一方面由于阻尼的存在,另一方面V∞较低并且系统的质量较小,所以并没有出现高速水翼以及机翼经历颤振时的结构损毁。

图6 舵系统振动幅度变化和振动频谱图Fig.6 Amplitude growth of the vibrations and frequency spectrums of the hydrofoil system
图7为V∞=1.0 m/s时舵系统振动时历曲线(见图7(a)和图7(c))和相轨线(见图7(b)和图7(d))。可见,系统的运动中存在着沉浮和俯仰两个成份,分别是系统对支撑弹簧回复力和扭转弹簧回复力矩的响应。由于V∞=1.0 m/s没有达到系统的临界颤振速度VF,所以系统进行衰减振动。系统的动能会在运动的过程中发生耗散,表现为系统沉浮和俯仰运动的幅度逐渐变小,直至达到稳定状态。从系统运动相轨线可以看出,沉浮成份表现为围绕原点做周期运动,由于振幅单调减小,所以相轨线不断持续向原点靠近,最终在原点达到稳定状态。而俯仰成份的周期运动围绕着一个飘移的中心进行。从计算结果来看,舵系统流致运动的沉浮成份是一种简谐振动,而俯仰成份为两个频率的耦合振动。

图7 V∞=1.0 m/s时,系统振动时历曲线和相轨线Fig.7 Time history cures and phase orbits of the hydrofoil system at V∞=1.0 m/s
经计算,舵系统的临界颤振速度为VF=2.37 m/s,图8(a)和图8(c)为系统发生颤振时的时历曲线图。可见,沉浮成份做等幅简谐振动,即运动的过程中不会发生能量耗散;而俯仰成份在经历了短暂的飘移振动之后,也进行和沉浮成份相似的等幅振动。这是颤振理论中典型的振动形态,在忽略阻尼的作用时,系统将进行无消减的等幅振动,如果航行体在高速运动中发生这种振动有可能造成结构的扭曲、损坏,还有可能产生较大的噪声导致降低航行体的性能。系统此时相应的运动相轨线,如图8(b)和图8(d)所示。沉浮振动和俯仰振动最终都演化为典型的极限环振动。因为系统在运动中不存在能量的耗散,所以能量在动能和势能之间不断转化。

图8 V∞=2.37 m/s时,系统振动时历曲线和相轨线Fig.8 Time history cures and phase orbits of the hydrofoil system at V∞=2.37 m/s
图9为利用未经参数修正的运动方程求解所得的非等截面系统发生颤振时的时历曲线图和相轨线。可见,系统运动的沉浮成份和俯仰成份都进行发散振动。沉浮成份以原点为中心做周期运动,但是与低流速时不同,运动轨迹不断向外扩散;而俯仰成份的运动轨迹在出现短暂的飘移后,也转化以原点为中心向外不断做周期性的扩散。理论上,出现这种情况是由于系统在运动的过程中不但没有发生能量耗散,还持续不断地从流体中吸收能量。这些能量由系统的动能转化为势能,又由势能转化为动能,如此循环往复便出现了系统运动过程中沉浮和俯仰成份振幅不断扩大的现象。与图8进行比较,可知在未进行参数修正的前提下,利用两自由度系统任意运动方程求解会导致VF偏小。
当来流速度V∞=5.0 m/s时,非等截面舵系统振动的时历曲线和相轨线,如图10所示。可见,系统振动的沉浮成份和俯仰成份都呈现发散状态,并且幅值迅速扩大。图10(b)和图10(d)为系统运动的相轨线图,沉浮成份和俯仰成份都以原点为中心做周期运动,运动轨迹不断向外扩散,并且扩散的速度不断增大。如果不考虑阻尼的影响,现实中的舵系统若在此流速下进行发散振动,则很可能因为沉浮和俯仰振幅的激增而遭到损坏。
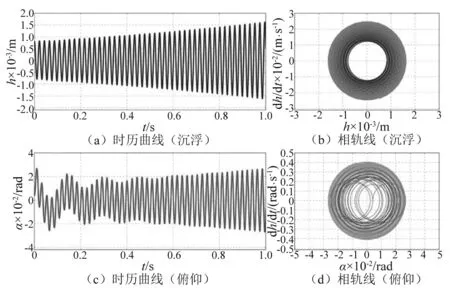
图9 V∞=2.37 m/s时,利用未修正方程求解的时历曲线和相轨线Fig.9 Time history cures and phase orbits of the hydrofoil system via unmodified equation for the vibrations at V∞=2.37 m/s
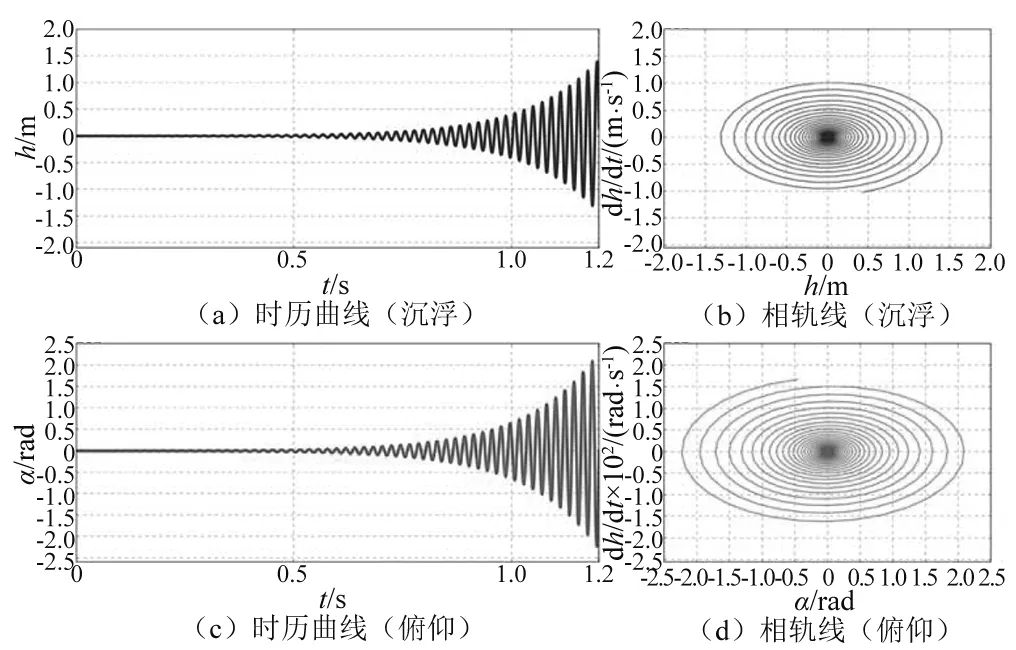
图10 V∞=5.0 m/s时,系统振动时历曲线和相轨线Fig.10 Time history cures and phase orbits of the hydrofoil system at V∞=5.0 m/s
2.2 绕流场分析
图11为V∞=1.0 m/s时舵附近的流场变化图。在运动最初(见图11(a)),舵的前缘出现零星的细小涡,但是并不明显,舵的后缘附近出现了细小的尾涡。t=0.05 s(见图11(b))时,在舵的前缘出现了明显的涡量变化,同时舵的后缘出现明显脱落涡。t=0.1 s(见图11(c))时,在舵上表面从前缘到刚心(约1/4弦长处)之间出现较大的涡量,而后3/4的上表面有形成多个细小的涡。t=0.15 s时(见图11(d)),在舵的上表面从刚心到后缘出现了明显的涡层。t=0.5 s(见图11(e))时,在舵的上表面,前缘和刚心之间的涡量继续增大,刚心和后缘之间的涡层不断扩大;在舵的下表面,也有出现涡层的趋势。由于系统的运动发生衰减,所以t=4 s(见图11(f))时舵趋于稳定,俯仰运动幅度锐减导致其尾部脱落涡消失,而沉浮运动幅度锐减导致涡集中在舵的后半部附近。

图11 V∞=1.0 m/s时,舵附近流场以及涡量云图Fig.11 Vorticity contours of the hydrofoil at V∞=1.0 m/s
图12为V∞=VF=2.37 m/s时舵附近的流场变化图。可见,在运动最初(见图12(a)),和衰减运动时相似,舵的后缘附近出现细小的尾涡,同时前缘也出现了零星的涡。t=0.05 s(见图12(b))时,舵的上表面前缘和半弦长之间出现了明显的涡量变化,并且刚心位置的涡最为突出,同时在尾部出现一系列明显的脱落涡。t=0.1 s(见图12(c))时,在舵的上表面,前缘和刚心之间的涡不断向后缘扩散,并在刚心和后缘之间形成了明显的涡层。此时舵的上表面形成一个完整的涡层,这与衰减运动时不同;在舵的下表面,在刚心和后缘之间也有形成涡层的趋势。t=0.15 s(见图12(d))时,舵上表面的涡层继续向后扩散,并与尾涡融合。t=2 s(见图12(e))时,舵出现大角度的俯仰运动,此时前缘和刚心之间出现加大的涡量,而刚心和后缘之间的涡层已经完全消失。t=4 s(见图12(f))时,只存在前缘附近的一个巨大涡,舵的上下表面几乎都没有涡形成。由于已经忽略了阻尼的作用,所以舵的俯仰运动继续加剧,而非经典的等幅运动。这不仅会大大降低航行体的操控性能,甚至有可能造成舵系统的结构损坏。

图12 V∞=2.37 m/s时,舵附近流场以及涡量云图Fig.12 Vorticity contours of the hydrofoil at V∞=2.37 m/s
3 结 论
本文通过对经典两自由度系统任意运动的无量纲动力方程进行参数修正,在计算中引入了展弦比对流体动力的影响。两自由度舵系统的流致振动实际上是动能和势能相互转化的过程,随着V∞的增加相轨线的形状越来越趋于扁平化,这意味着系统的动能可以转化为更大的势能。这是因为低流速时,系统的动能会产生耗散,致使系统进行衰减振动;当流速达到VF时,系统的动能可以全部转化为势能,势能亦可全部转化为动能,从而出现极限环形式的相轨线;而在高流速下,系统的动能不但不会发生耗散,还会在振动过程中不断从流体中吸收能量并将其转化为势能,使得系统振动相轨线不断向外扩散。
低质量比舵系统发生颤振时,系统的振动形态从稳态转化为非稳态。在对应的频谱图上,系统的沉浮频率或俯仰频率附近会出现一个新的频率,表明在这个过渡期间系统的运动受到了一定程度的扰动,但是并没有像高质量比系统那样形成一个突出的频率,这是低质量比系统和高质量比系统颤振现象的主要区别。
通过数值模拟,发现在舵系统运动最初,舵的后缘附近会出现一系列细小的尾涡。并且,在舵的前缘会出现了明显的流体分离,这种分离不断向后缘扩散,同时会在舵的尾部出现一系列脱落涡。当系统进行衰减运动时,则尾涡会随着系统的静止而消失,舵上表面的涡层主要出现在1/4弦长处和后缘之间。如果系统进行发散运动,则舵会发生剧烈运动,其前缘附近产生巨大的涡,涡层遍布舵的整个上表面。并且在1/4弦长处会出现明显层流分离现象,这与衰减运动不同。
