高速列车牵引传动系统机电耦合振动特性研究

赵心颖， 林 飞, 杨中平， 李翔飞， 张志强， 焦京海

(1. 北京交通大学 电气工程学院， 北京 100044； 2. 中国中车青岛四方机车车辆股份有限公司 技术中心， 山东 青岛 266000 )

高速列车的牵引传动系统是一个机电耦合的复杂系统，其作为列车高速运行的动力来源，直接关系到列车的正常运行。传动系统中电气部分主要功能是实现电能变换，将从受电弓接收到的电能，转换为适合牵引电机的频率和幅值均可调的电能，从而驱动电机转动；机械部分的主要功能是将电机输出的转矩准确并有效地传递到轮对，最终牵引列车前行[1]。在列车牵引运行过程中，牵引电机输出转矩在驱动装置中传递，由于传动环节各部件并非完全刚性，在旋转过程中产生不同大小和相位的瞬时转速起伏，导致传动装置扭转振动，影响各机械部件的使用寿命，不利于列车的安全运行。

文献[2]针对万向轴驱动系统的非线性振动特性进行研究分析，为避免由于扭转振动产生的影响；文献[3]重点分析在轨道不平顺激励条件下振动特性；文献[4]提出一种基于电机转矩估计的扭转振动检测方式。但是针对电气激励下驱动装置的振动特性研究相对较少，荷兰学者M.W.Winterling[5-7]通过理论与仿真计算万向轴驱动系统的振动模态，研究电机的谐波转矩特性以及两者的耦合关系，并对轨道激励下的驱动装置振动特性进行仿真分析，但未进行实验验证。文献[8-9]对架悬式驱动装置进行分析，研究整车在电机谐波转矩和轮轨黏着特性共同作用下的动力学特性，但未对驱动装置各子部件(牵引电机、齿轮箱等)振动情况进行建模分析。

本文考虑驱动装置电机矢量控制、齿轮箱弹性悬挂产生的扭转-弯曲耦合振动，联轴节、车轮等各部件之间的力学关系建立了高速列车牵引传动系统机电耦合振动模型；分析机械结构振动模态和电机电流谐波与转矩脉动特性，从而对机电耦合关系进行详细研究；根据实际列车参数在SimMechanics中搭建耦合振动仿真模型，进行仿真验证；采用基于误差电压的死区补偿方式，实现了机电耦合振动抑制；搭建实验平台，验证理论与仿真有效性。

1 传动装置机械振动模态分析

高速列车驱动装置主要包括电机、联轴节、齿轮箱、车轴、轮对以及悬挂装置等部分，见图1。目前常用的轴系模型可以分为分布质量模型和集中质量模型[10]，由于针对驱动装置中的轴系振动特性进行研究，故选用集中质量模型。

扭转振动的状态变量为驱动装置各部分转过的角度，但在实测过程中，振动特性主要通过对横向、纵向和垂向振动测量得到，即反映的是系统的弯曲振动特性。因此本部分考虑系统扭转与弯曲耦合振动关系对系统进行建模分析。

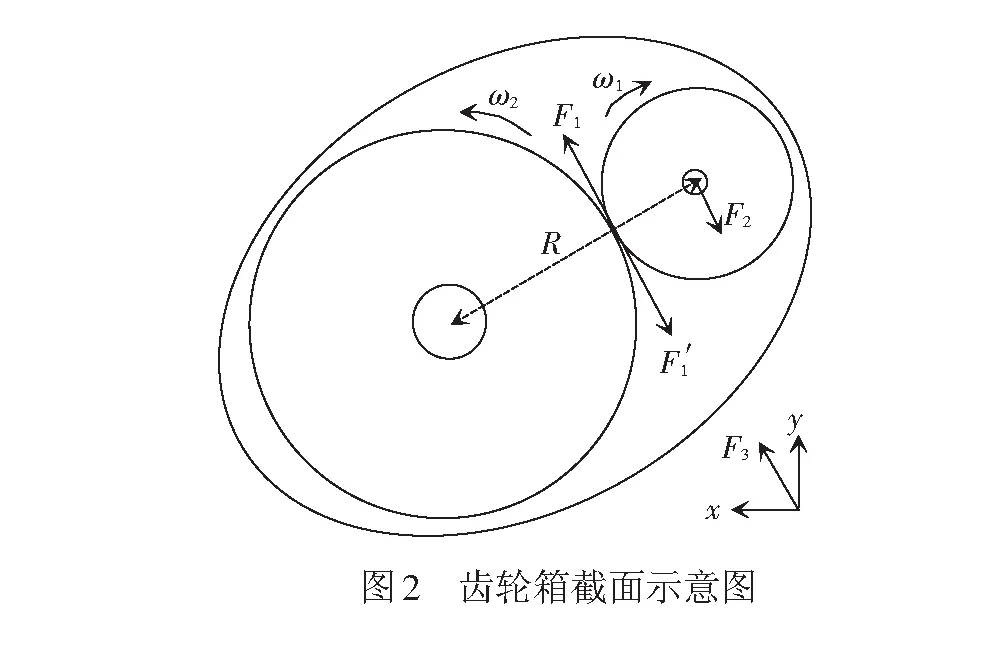
考虑齿轮箱的运动状态，将主动轮和从动齿轮结合考虑，同时由于车轴的扭转阻尼比较大，可将其与车轮等效为一体，以CRH2A型车为例，通过合理的简化，图1的等效结构见图3，集中质量块视为轮盘，各轴段只考虑其抗扭刚度，而不考虑其转动惯量(已平均分配到左右轮盘上)。

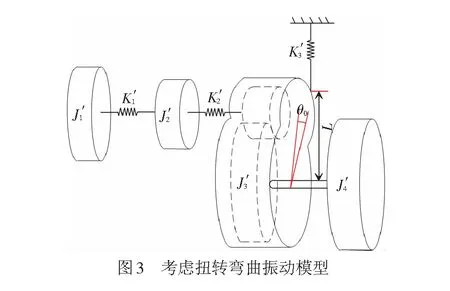
图3中各部分参数的含义见表1。

表1 模型扭转刚度列表

设θ1、θ2、θ3、θ4和θ5分别为电机转子、联轴节、小齿轮、齿轮箱以及车轮和大齿轮转动的角度，齿轮传动比为n。小齿轮的运动状态包括沿自身中心的“自转”和沿车轮中心的“公转”，其转速关系式为

( 1 )

不考虑系统的激励源和阻尼构建系统状态方程，选取各部位的转动角度θ为状态变量，表达式为

( 2 )

将式( 1 )代入式( 2 )，计算固有振动频率。

采用Matlab软件中的SimMechanics模型对驱动装置进行建模，考虑系统阻尼后，系统存在3个谐振峰值点，其谐振峰值频率值和增益值见表2。

表2 扭转-弯曲振动的阻尼振动频率和峰值增益

3 高速列车牵引电机谐波转矩分析

以CRH2A型车为例，其采用多模式脉宽调制的控制方式，见图4。

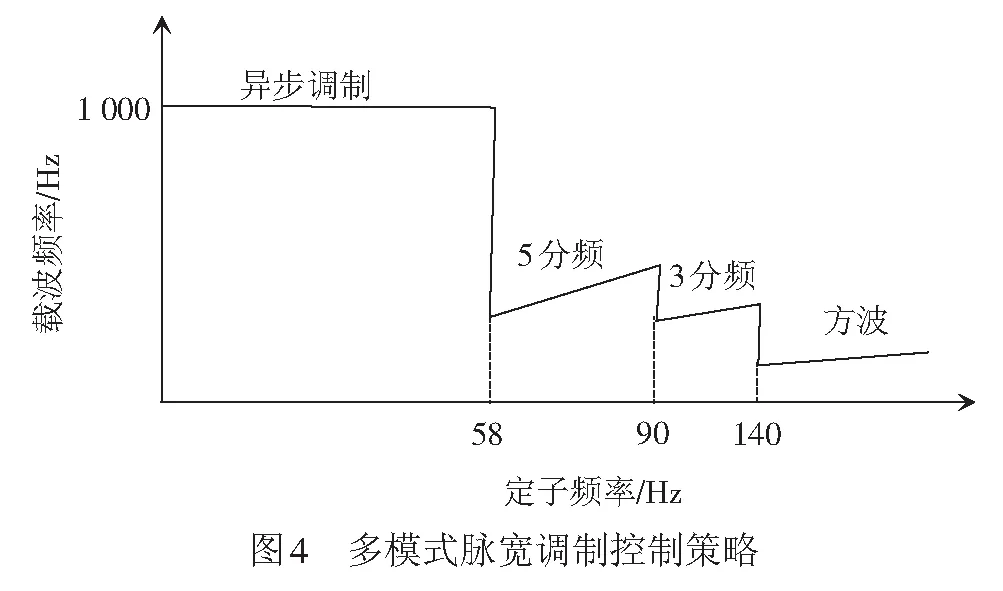
对理想情况下各调制方式下的谐波转矩进行分析，结果见表3。

由于分段同步区和方波区产生的谐波转矩频率主要为定子频率的6倍，而在第二节分析了驱动装置的固有频率为：4.87，24.2，52.39 Hz,因此当定子频率为0.81，4.03，8.73 Hz 时，系统可能产生共振。而此时定子频率远低于进入分段同步调制阶段的频率，因此当轴系发生共振时，列车应处于异步调制阶段。故主要考虑异步调制阶段对低频转矩脉动成因进行分析。

表3 不同调制方式下电机转矩脉动

在实际应用中，功率开关器件不是理想开关，存在一定延时，为保证桥臂不会出现直通，必须设置死区时间。死区效应分为开关死区效应和控制死区效应，一般情况下开关死区效应较小，可以忽略，因此只需考虑控制死区时间Td，死区导致的逆变器误差电压分析见图5。

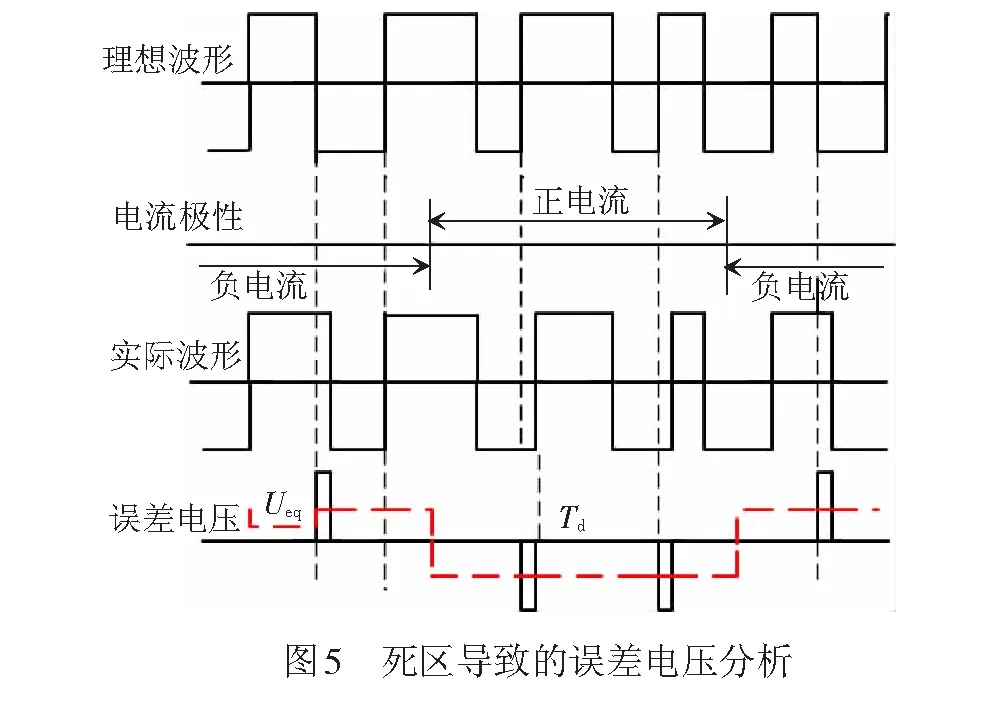
将上述每个电流周期内误差电压脉冲等效为一个矩形波电压，可得幅值Ueq为

( 3 )

式中：m为一个定子周期内的载波周期数；Td为死区时间；Ts为定子电流周期；Ud为直流侧电压。

误差电压傅里叶级数展开式为

( 4 )

式中：ω为基波频率；n为非3的倍数的奇数。

由式( 4 )可得，死区导致逆变器输出电压含有5、7等非3的倍数奇数次谐波，其含量与死区时间成正比。

搭建Simulink仿真模型，设置仿真条件为列车运行速度100 km/h。通过仿真结果可得，死区效应导致定子电流中存在明显的5次谐波。对比不同死区时间下5次谐波的含量，见图6，5次谐波含量与死区时间成正比。

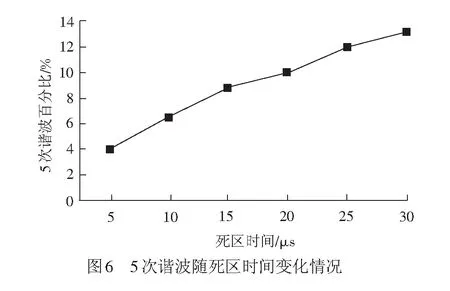
电机定子谐波电流会导致转子中感应出相应的谐波，而转子谐波电流与气隙基波磁通作用产生的谐波转矩影响最大，以5次转子电流谐波为例进行分析，根据电磁转矩的计算原理[12]，可得电机每相产生的转矩的瞬时值为

TeB5=

TeC5=

( 5 )

式中：np为极对数；Eg为气隙基波磁通感应电动势有效值；Ir5为转子5次谐波电流有效值；φr为气隙基波电动势和转子5次谐波电流的夹角；fs为电机定子基波频率；TeA5、TeB5、TeC5分别为电机三相5次电流谐波产生的谐波转矩瞬时值。

将式( 5 )简化后合并，可得5次电流谐波产生的谐波转矩瞬时值为

( 6 )

由式( 6 )可得，5次电流谐波产生的振动谐波转矩频率为6倍基波频率。

对不同死区时间下的转矩脉动幅值进行统计，见图7。系统转矩脉动幅值的范围随着死区时间的增大而不断增大，其脉动峰峰值从360 N·m增加到510 N·m，同时其幅值增加基本呈现线性变化。

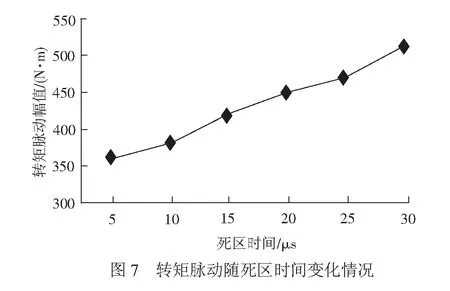
4 传动系统机电耦合振动

4.1 传动系统机电耦合振动分析

对电机谐波转矩激励下的驱动装置受迫振动特性进行分析，不考虑系统阻尼，建立驱动装置在电机转矩作用下的状态方程

( 7 )

式中：J为转动惯量矩阵；K为扭转刚度矩阵；F0为激励矩阵；ωj为激励频率；θ为各部件转动角度矩阵。

则其特解形式为

θ=B·eiωjt

( 8 )

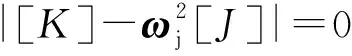
由此可得当激励频率接近系统的任何一个自由振动频率时，都会引起系统共振。

采用Matlab进行机电联合仿真，设置仿真时间为10 s，速度不断增加，观察列车各个驱动装置在不同速度下的振动情况。死区时间分别为5 μs和15 μs条件下的电机转子角加速度特性，见图8。

通过图8(图中红圈标注区间,下同)仿真结果对比，当列车运行到某个速度点时，振动情况明显加剧，其振动峰峰值大于100 rad/s2，振动频率以50 Hz左右为主。

图9为联轴节的振动情况，如图中的圆圈所示，其存在两个振动明显加剧的时间段，该两部分的对应频率分量与表2中的ω2bend=24.2 Hz和ω3bend=52.39 Hz相对应。

齿轮箱和车轮角加速度波动情况分别见图10、图11，其波动明显减弱。

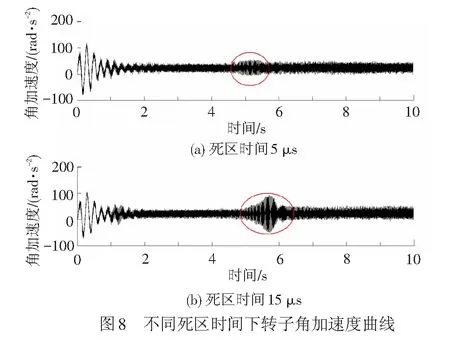
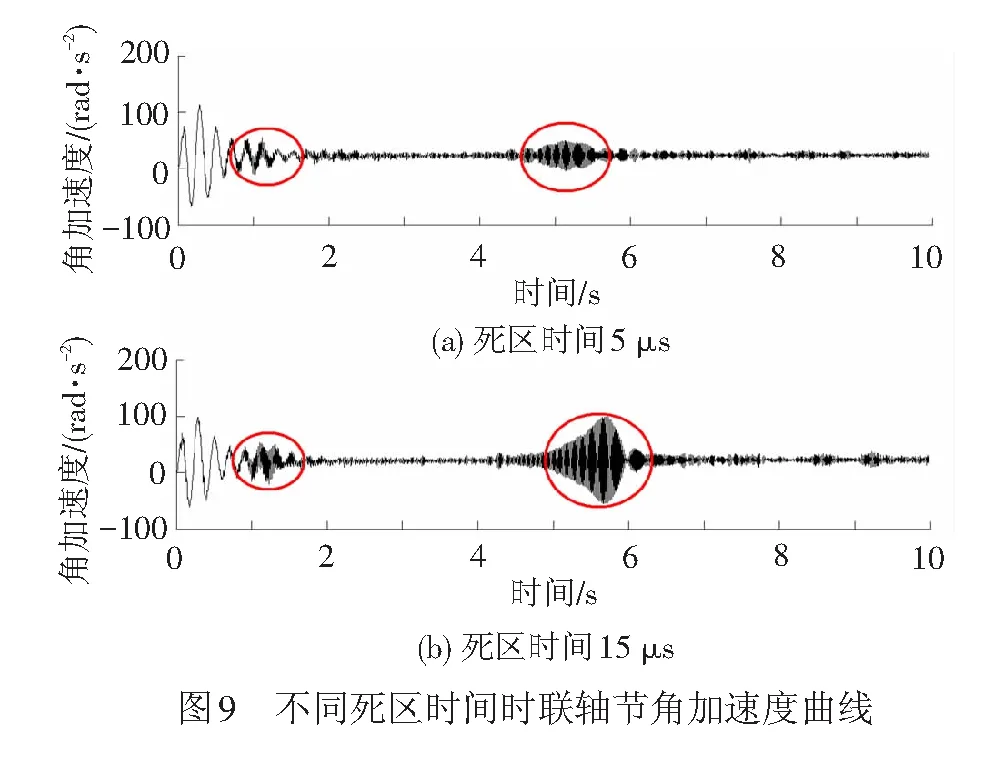
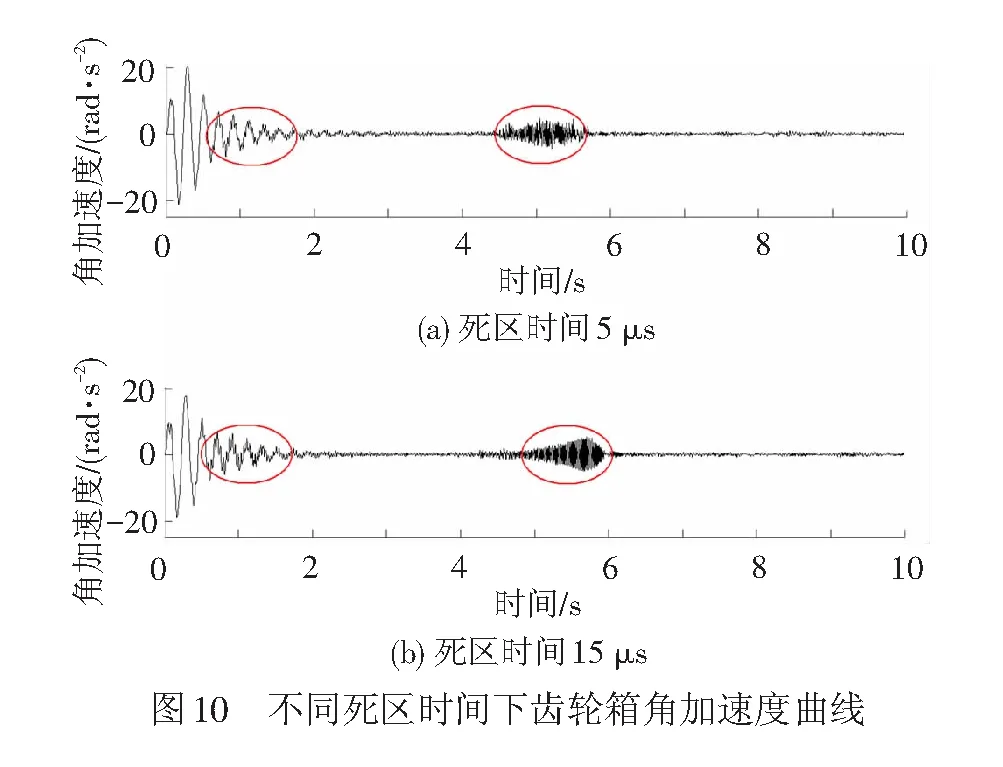
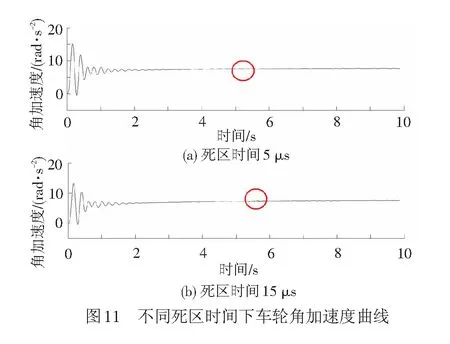
通过图8～图11的对比可知：(1)当电机运行到共振速度时，若电机转矩中谐波频率与驱动装置固有振动频率相近，轴系耦合振动会明显加剧，其振动峰峰值约增加1倍；(2)由电机转矩脉动产生的振动，驱动装置中越靠近电机的部分其角加速度波动情况越剧烈，转动惯量越小，振动越剧烈；(3)随着死区时间的增加，驱动装置受迫振动峰峰值会明显增大。

4.2 传动系统机电耦合振动抑制策略

从电气角度而言，系统机电耦合振动主要与电机低频谐波转矩相关，故抑制振动的主要方式是对逆变器死区效应进行抑制。

目前针对逆变器死区补偿方式主要为两种：基于误差电压补偿[13-15]和基于脉冲补偿[16-17]。导致电机谐波转矩中存在低频分量的主要原因是逆变器输出的实际电压与理想开关情况下的误差，故本节采取误差电压死区补偿方式，其具体控制框图见图12。

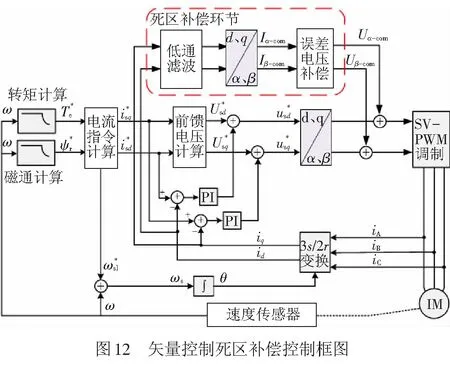
通过α、β轴的电流值可以确定电流矢量的实际位置，通过电流矢量所处的位置可以确定三相电流的方向，从而确定Uα和Uβ补偿值。

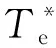
借鉴SVPWM的开关状态与电压空间矢量的关系，同样可以针对电流矢量进行分析，由于要通过电流矢量的位置来确定三相电流的方向，故需对电流矢量进行重新分区，其具体分区方式见图13。

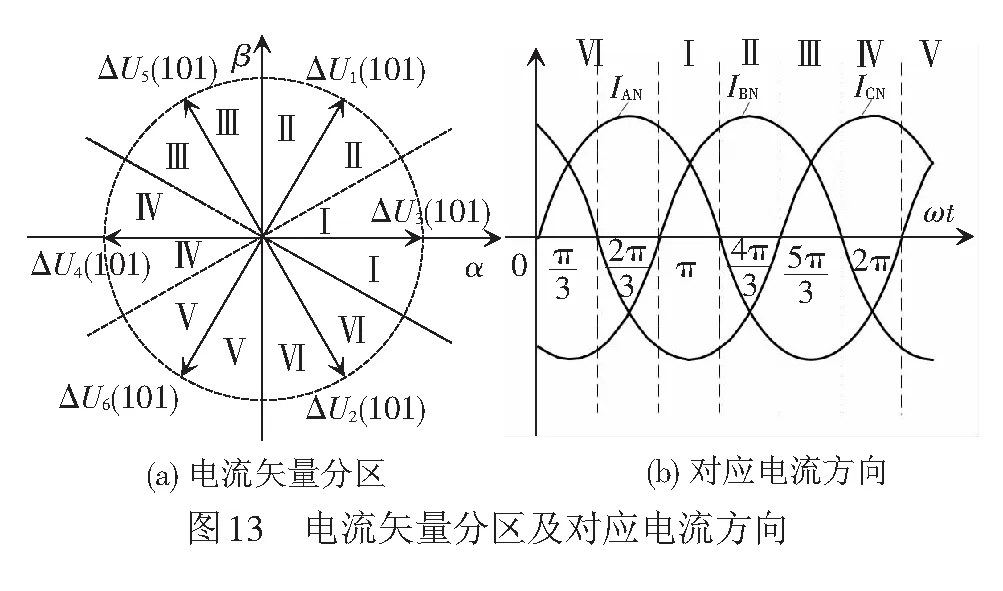
图13中：ΔUi为非零基本电压空间矢量,i=1,2,…,6;IAN、IBN、ICN分别为三相额定电流。得到三相电流的方向后，即可确定三相电压的具体补偿值，每个开关周期Ts内的等效误差电压的幅值Uer为

( 9 )

由图5可知当相电流的方向为正时，相电压波形较之理想情况下的波形变窄，而当电流方向为负时，正好相反，故每相的补偿电压值Up-com为

(10)

式中：ip为相电流。

根据3s/2s变换，可以计算出，在α、β轴上应该补偿的电压值为

(11)

式中：UA-com、UB-com、UC-com分别为电机三相电压。

由此可以得到在不同电流矢量扇区内的补偿电压值。

加入死区补偿环节进行仿真验证，对比电机A相实际电流和补偿电压之间的对应关系，见图14。由此可得补偿电压的相位与电流相位基本一致。

通过对比补偿前后电机A相电流的FFT分析结果(见表4)，未补偿死区时，电流存在明显的5次和7次谐波，而补偿后5次谐波得到的明显的抑制，其含量已经由1.8%下降到0.2%。

表4 死区补偿前后电流谐波特性对比 %

耦合条件下的弯曲-扭转振动模型中齿轮箱的角加速度情况同样可以验证死区补偿的效果，见图15。

5 实验结果及分析

5.1 机电耦合振动实验

由于不具备整车线上试验的条件，因此在实验室搭建传动系统耦合振动实验平台，在牵引电机和负载电机中加入齿轮传动装置，并在齿轮传动装置的垂向加装振动加速度传感器，用于测量其振动状态。高速列车上大齿轮侧环抱在车轴上，小齿轮侧的吊鼻通过吊杆与构架上的吊座相连接，而在吊杆的两端加入防振橡胶，一定程度上缓解齿轮箱的振动与冲击，因此在齿轮箱和台架中加装了10 mm厚的弹性材料(橡胶)。由于齿轮箱的传动比为4∶3，在牵引侧选用4极电机，负载侧采用6极电机，电机和齿轮箱的连接采用梅花形联轴节。本装置无法完全模拟实车驱动装置结构和运行条件，但能证明由低频转矩脉动所产生的机电耦合振动现象，并验证抑制策略的有效性[18]。

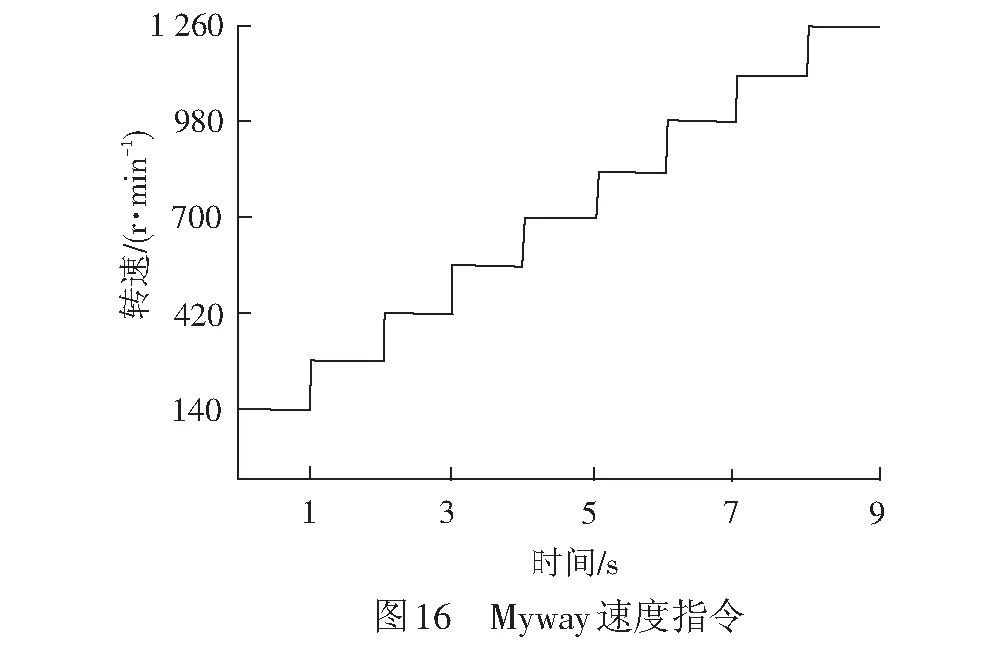
设置负载电机的负载转矩为5 N·m，牵引电机的速度指令变化见图16。

当死区时间为5 μs时，对振动信号进行短时傅里叶分析，结果见图17。

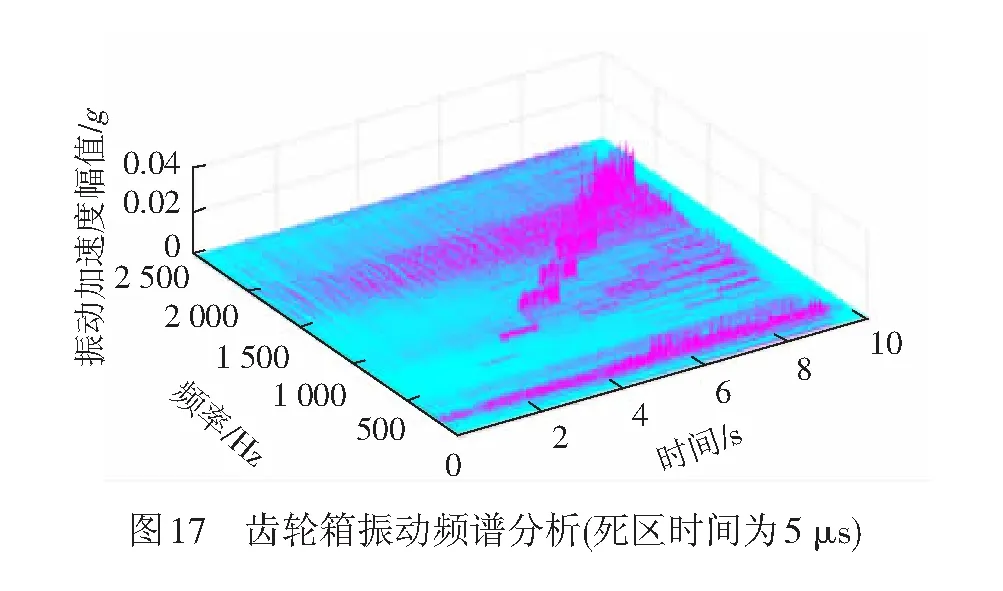
由图17可得，振动中存在不随速度变化的频率成分，即系统的固有振动频率，主要体现在180 Hz左右，该频率的振动在5～6 s内明显加剧，增加了一倍左右。这是因为当电机谐波转矩的成分为180 Hz时，系统产生共振使得振动明显加剧，此时电机的定子频率为30 Hz，通过对于转速的归算，约在850 r/min附近，通过图17可以得到系统在5 s时的转速为840 r/min，此时的电机输出谐波转矩的成分刚好与实验装置的固有振动频率相近，导致振动的加剧。

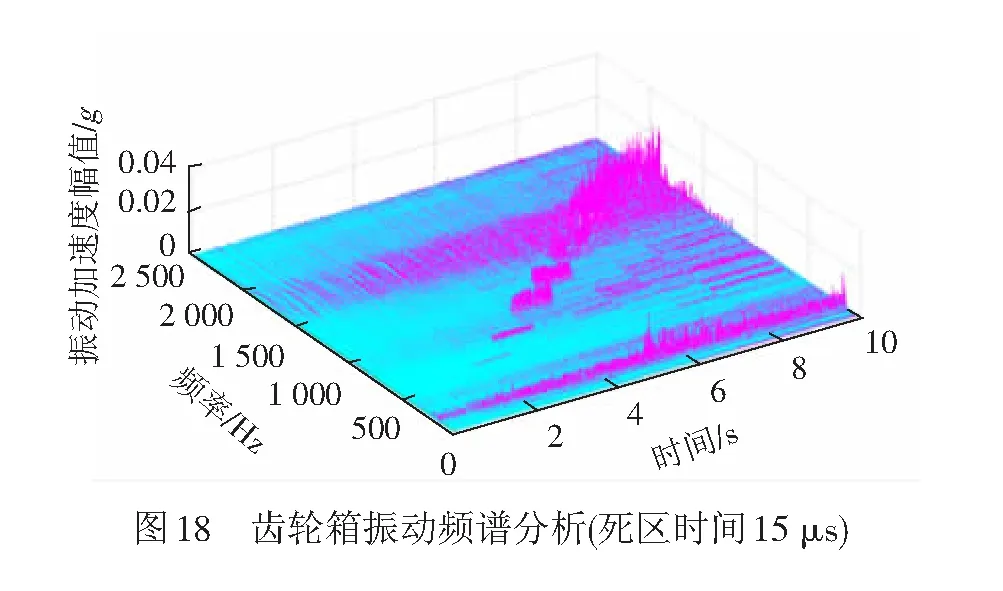
当死区时间增加至15 μs时(见图18)，可以得到类似的振动趋势，相比于5 μs，其在5～6 s时振动的峰值增加了20.59%。

5.2 死区补偿实验

在该实验平台上进行死区补偿实验，为与仿真对应，亦选取死区时间为15 μs。图19为死区未补偿时电流波形，在电流过零点时出现了明显的零电流钳位现象[19]，而采用死区补偿策略后，电机A相电流和补偿电压的波形见图20，补偿电压的相位与电流相位基本一致，对其进行FFT分析，补偿前后的对比结果见表5，证明死区补偿策略的有效性。

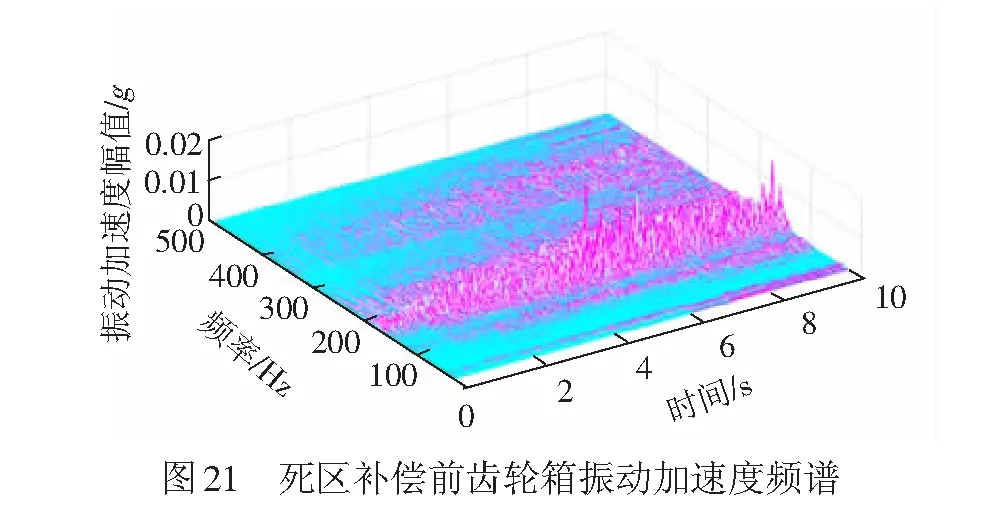
将图18所示傅里叶分析结果取局部频率，见图21，补偿后振动波形见图22。

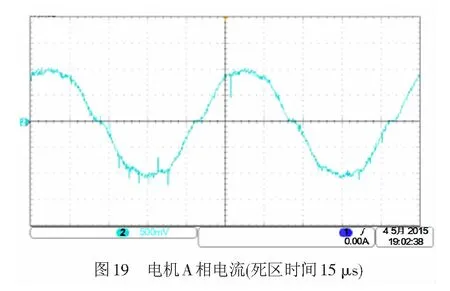
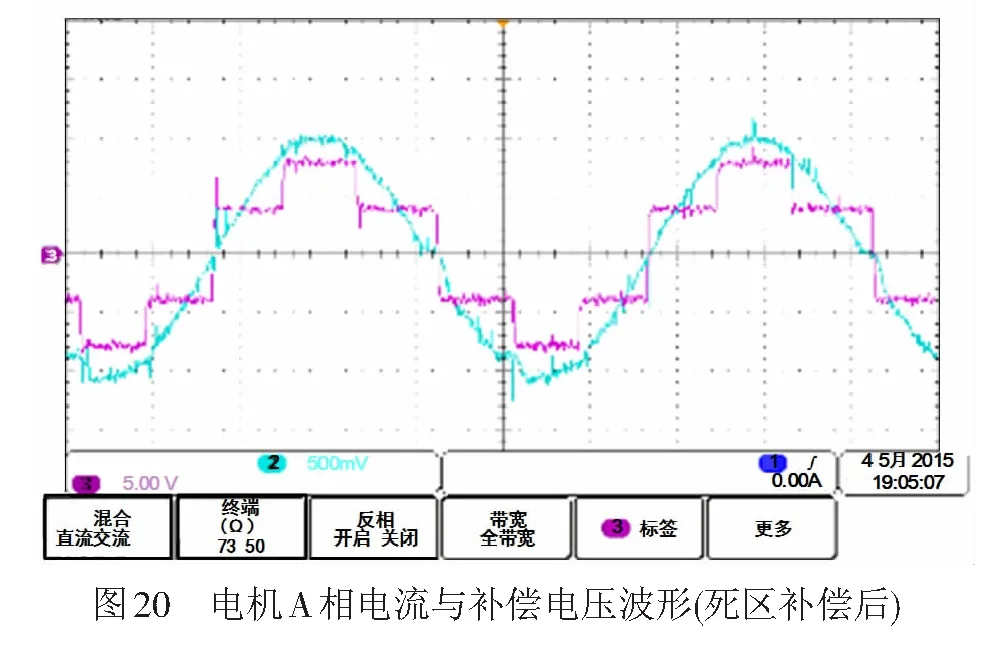
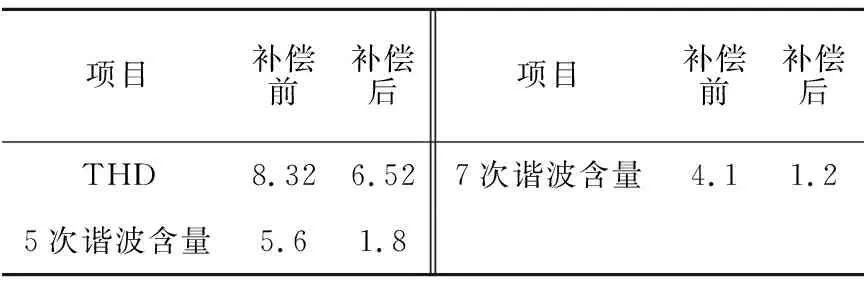
表5 死区补偿前后谐波特性对比 %

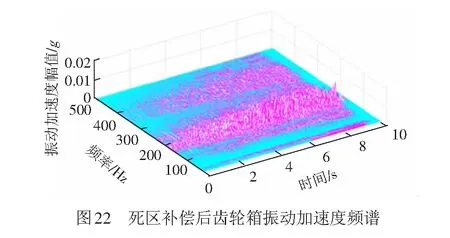
在5～6 s内补偿后的振动峰值有所减小，减小了25.61%，5 μs时的补偿结果也有所减弱，减小了10.29%。

6 结论

(1) 建立了传动系统驱动装置振动模型，驱动系统存在3个振动的固有频率，这3个频率均较低。

(2) 开关死区在电机电流中主要产生5、7次谐波，在转矩中会产生6倍定子频率成分谐波转矩。

(3) 当电机运行到共振速度时，电机输出转矩中含有与驱动装置固有振动频率相应的成分，此时驱动装置振动明显加剧。振动程度与死区时间成正比，且在驱动装置中越靠近电机侧、转动惯量越小，振动越剧烈。

(4) 搭建机电耦合振动实验平台，其固有频率相比于列车要大得多，实验主要针对系统的一个固有频率进行了分析。当电机输出转矩中含有与固有频率相等的谐波成分时，驱动装置振动明显加剧，振动峰值随着死区时间的增加而增加，且死区补偿策略对于耦合振动有抑制作用。