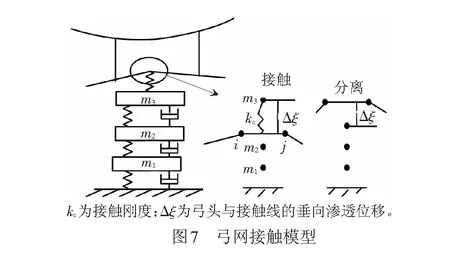
基于弓网动力仿真的160 km/h刚柔过渡系统方案研究
2018-09-28关金发田志军吴积钦
关金发, 田志军, 吴积钦
(1. 西南交通大学 电气工程学院, 四川 成都 610031; 2. 中铁第一勘察设计院 电化处, 陕西 西安 710075)
刚性接触网在隧道内相对柔性接触网具有一定优势,其接触线无张力,不用设置下锚装置,不会发生断线事故,零部件少,载流量大,安全可靠,维修工作量小等,被广泛地应用于地铁隧道内[1]。自2002年广州地铁2号线刚性接触网试挂成功后,刚性接触网逐步替代柔性接触网,成为城市轨道交通隧道内架空接触网的主要形式。上海地铁6、8、9、10、11号线;广州地铁2、3号线;南京地铁1号线;成都地铁1、2号线;北京地铁14号线等工程均采用刚性接触网[2]。在干线铁路中,石怀线电气化扩能工程、新建兰武二线乌鞘岭隧道等刚性接触网均得到良好的应用[3]。
隧道内外结合部存在刚性接触网与柔性接触网转换的过渡段,称为刚柔过渡。受电弓通过该区域的弓网动力性能一般较差,属于接触网的薄弱环节。国内外学者对受电弓与刚性接触网的研究主要集中在受电弓与刚性接触网建模及弓网动力响应分析上,针对刚柔过渡结构的研究较少。梅桂明[4]通过对刚性-刚柔-柔性悬挂接触网、受电弓动力学仿真,发现弓网间接触力在刚柔过渡段出现较大波动。王世轩[5]建立了贯通式和锚段关节式2种刚柔过渡仿真模型,得出了不同速度等级下受电弓由柔性接触网过渡至刚性接触网在过渡区的接触力均比反方向波动大。赵正路[6]针对石怀扩能工程中刚柔过渡弓网关系较差的问题,利用施工误差的大小及方向调整了刚柔过渡接触线高度,该调整方案通过了冷滑试验。T.Kobayashi[7-8]通过研究原有锚段关节式刚柔过渡不能满足更高速度的弓网动力性能,设计一种新型锚段关节式结构,在柔性接触网处增加刚性汇流排或采用贯通式刚柔过渡方案,通过跑车试验,论证了新结构的运行性能可达130 km/h。Furrer[9]提出了一种贯通式刚柔过渡结构。部分学者建立了弓网有限元模型,研究刚性接触网悬挂结构质量、运行速度、跨距、汇流排坡度、弓网接触刚度、受电弓弓头质量等单因素变化的弓网动力响应[10-15]。综上所述,尚未见有关160 km/h刚柔过渡系统方案的研究。
随着城市轨道交通的发展,电气化列车的运行速度将增加,随之产生的问题是速度更快的受电弓是否适应当前的刚性接触网结构。基于此,本文分析既有刚柔过渡的结构,进行刚柔过渡仿真模型的建立,研究160 km/h及以上速度的受电弓与刚性接触网、刚柔过渡区段、柔性接触网动力相互作用,为研制160 km/h受电弓与刚性接触网系统方案提供前期研究基础。
1 既有刚柔过渡结构分析
简单的把接触网等效成连续垂向质量弹簧系统,柔性接触网的刚度要比刚性接触网的小,为使受电弓平稳地通过过渡区段,过渡区的刚度应是渐变的,工程中使用刚柔过渡汇流排使刚度渐变,见图1,通过从刚性接触网到柔性接触网按照从密到疏依次在汇流排上开槽实现。

既有刚柔过渡有2种实现方式(见图2):一种是锚段关节式过渡,即刚性接触网与柔性接触网是两支悬挂过渡,其工作原理是柔性接触网进入隧道后承力索拉出下锚,接触线上安装刚柔过渡汇流排然后下锚,与刚性接触网利用空间几何关系使受电弓顺利通过;另一种是贯通式过渡,即刚性接触网与柔性接触网合为一支接触悬挂,其工作原理是柔性接触网进入隧道时承力索于隧道口或内部下锚,接触线上安装刚柔过渡汇流排然后直接接入刚性接触网。
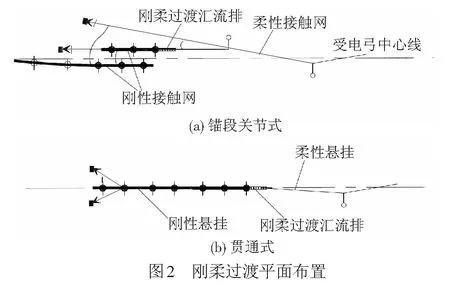
刚柔过渡的刚性接触网一般使用8 m Π型截面铝合金汇流排,定位悬挂为门型结构或腕臂式结构,锚段中间设中心锚结,其中定位点的刚度均较大。
城市轨道交通柔性接触网一般使用双接触线悬挂,而干线铁路柔性接触网使用单接触线悬挂。柔性接触网线索材料和张力组合与供电制式和速度等级相关。
2 刚柔过渡结构的弓网仿真模型
考虑弓网仿真模型与实际弓网系统存在误差,为研究满足160 km/h刚柔过渡结构,目标速度应适当增加,留有余量,本文设定为180 km/h。
既有动车组的设计最高运行速度为250 km/h,实际最高运行速度为200 km/h,与本文设定值接近,基于此,假设本研究的对象为动车组。与之配合使用的受电弓型号为DSA250。故以下以DSA250型受电弓为例,设计与之匹配的刚柔过渡。
DSA250型受电弓的动力仿真模型为图3所示的三质量-刚度-阻尼集中质点模型,其中m1~m3、k1~k3、c1~c3分别为下臂杆、上框架和弓头的质点归算质量、刚度和阻尼;fc、f0分别为弓网接触力和静态抬升力;y1~y3分别为下臂杆、上框架和弓头的质点位移。具体模型参数见表1。三质点受电弓的动力学方程为二阶微分方程组
( 1 )
式中:Mpa、Cpa、Kpa为受电弓的质量、阻尼和刚度矩阵;ypa为受电弓的位移矩阵;Fcpa为外力矩阵,包括静态升弓力和接触力。
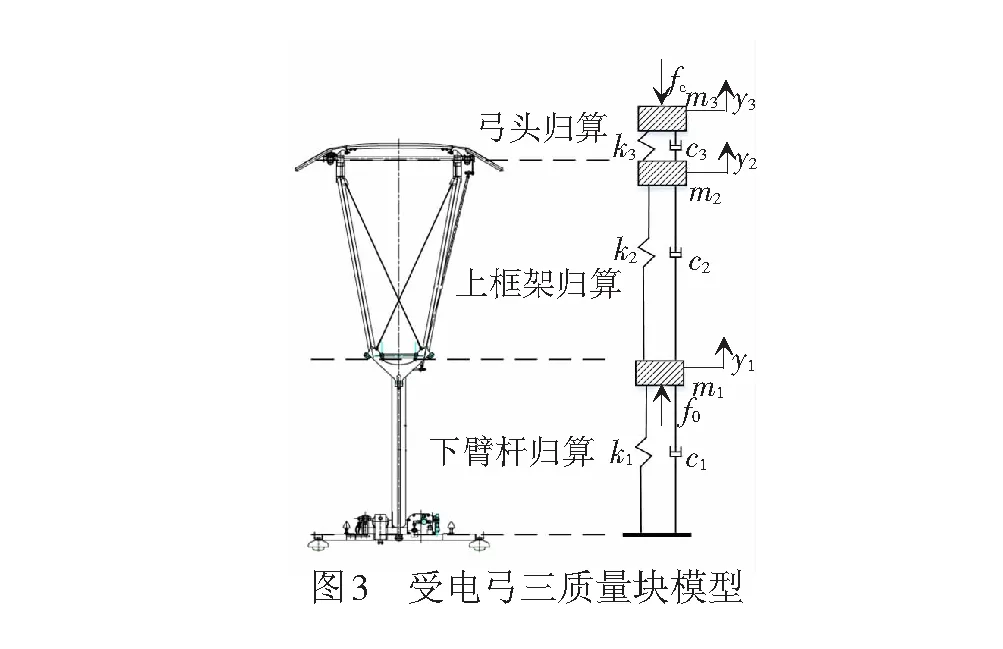
动车组上的受电弓数量视用电量而定,8节车使用1架受电弓,16节车使用2架受电弓。本文针对双弓进行研究,若双弓满足弓网动力性能要求,则单弓也满足。动车组双弓间距取200 m。
使用刚性接触网的线路中,广州地铁3号线北延段的运行速度较高,为120 km/h,实际弓网运行受流良好。以此刚性接触网结构与参数为参考,见表2,建立刚性接触网动力仿真模型。刚性接触网的定位点悬挂刚度设定为一个较大的值。
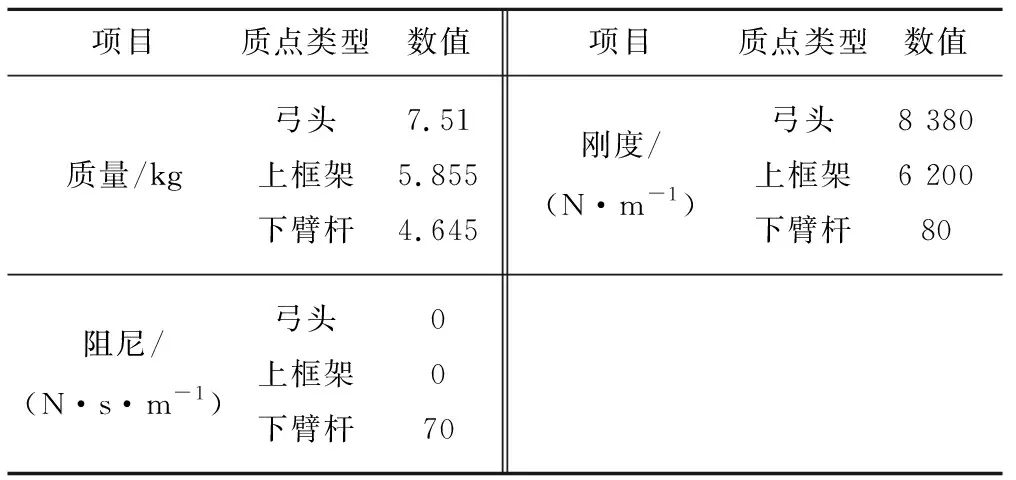
表1 DSA250型受电弓质点系模型参数
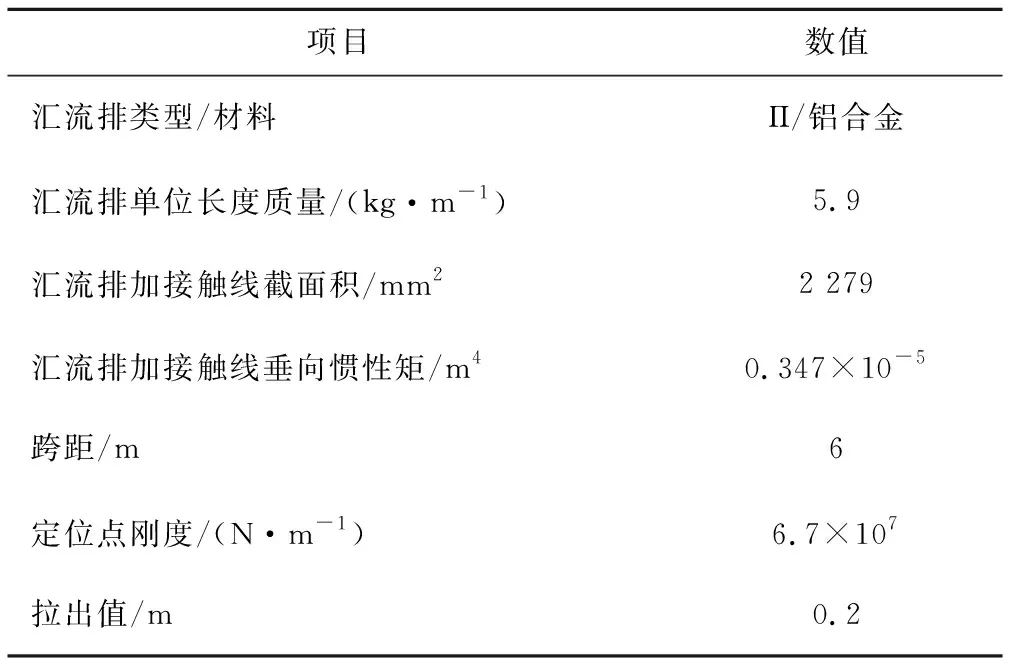
表2 刚性接触网参数
接触网作为牵引供电系统的载体与电流制式密切相关。由于运行速度为160 km/h,其相应铁路线路较长,宜采用交流供电方式。此时,柔性接触网的结构可参照干线铁路。
参照德国联邦铁路,与DSA250型受电弓匹配的接触网型号为Re250,以该接触网型号的结构及参数(见表3),建立柔性接触网动力仿真模型。
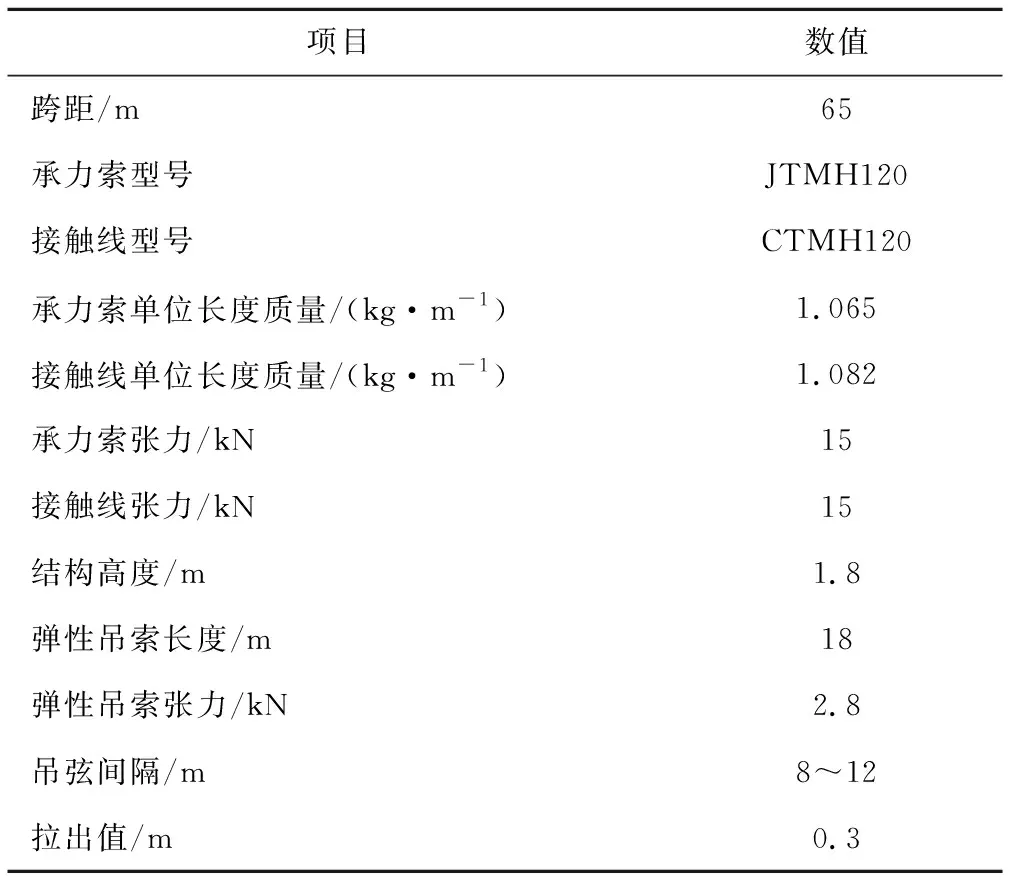
表3 Re250柔性接触网参数
不同刚柔过渡方式,均需利用刚柔过渡汇流排,刚柔过渡动力仿真模型的重点是处理刚柔过渡汇流排。观察图1刚柔过渡汇流排按一定距离开切槽,且切槽深度逐渐变大,每个槽的高度、截面和惯性矩都在变化,其高度变化规律见图4,一共有6个槽,槽1最浅,槽6最深,不同高度的截面积和惯性矩见表4。
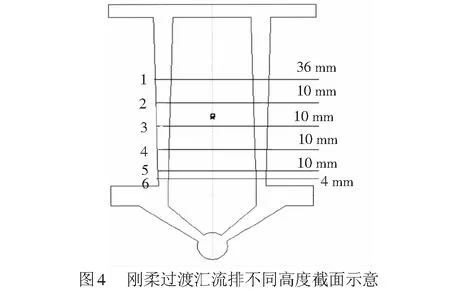
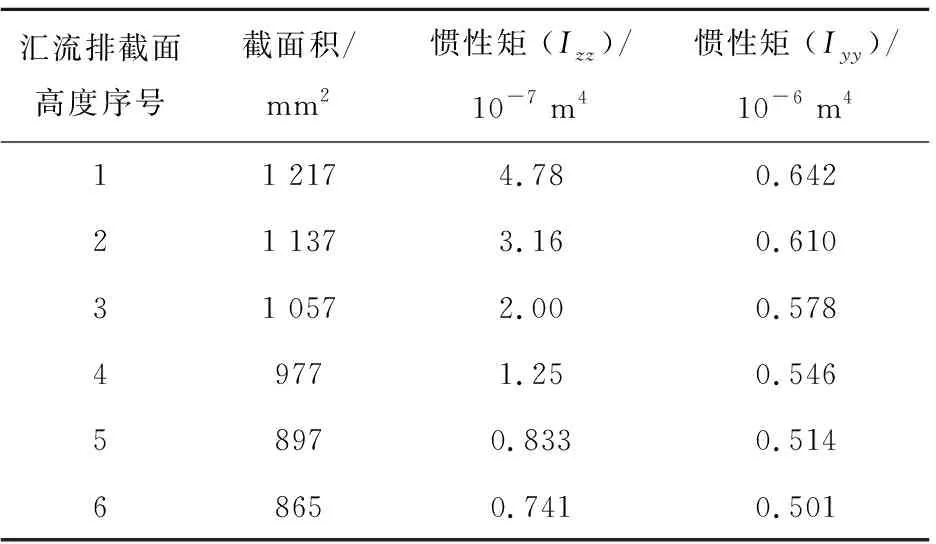
表4 不同截面高度汇流排参数
利用有限元法,将刚性接触网、柔性接触网和刚柔过渡汇流排等各结构离散成有限单元,建立统一的动力学仿真模型。
由于接触网沿线路布设,其长度相对截面大得多,故将刚性接触网的汇流排和接触线共同等效成空间梁单元,柔性接触网的接触线、承力索、弹性吊索和定位器分别等效成空间梁单元。刚性接触网的定位悬挂结构等效成弹簧单元。柔性接触网的吊弦等效成仅受拉不受压的索单元。
刚柔过渡模型的边界条件为:(1)刚性接触网的定位点弹簧悬空节点全自由度约束,中心锚结定位点全自由度约束,所有定位点约束线路方向和垂直线路方向的转动自由度;(2)柔性接触网的定位器一端连接接触线,一端约束除线路方向和垂直线路方向转动自由度外的自由度;(3)柔性接触网的承力索支持点约束除线路方向平动自由度外的自由度;(4)柔性接触网的接触线和承力索在刚柔过渡一侧的下锚节点约束所有自由度,在另一侧的下锚节点约束除线路方向平动自由度外的自由度。
刚柔过渡模型的初始条件:(1)柔性接触网线索张力引起的几何刚度;(2)柔性接触网接触线和承力索补偿张力;(3)所有单元的重力。
将所有梁单元、索单元和弹簧单元进行整体坐标转换及组装,得到刚柔过渡接触网的动力学方程式
Gf+Fcf+FTf
( 2 )
式中:Mf为接触网的质量矩阵;uf为接触网的节点位移坐标;K为接触网的弹性刚度矩阵;Kct为柔性接触网接触线、承力索和弹性吊索的几何刚度矩阵;Kd为吊弦的变刚度矩阵,当吊弦受拉时,刚度为轴向拉伸刚度EA/l,受压时,刚度变为10-6N/m;Gf为接触网的重力矩阵;Fcf为接触力矩阵;FTf为柔性接触网节点张力矩阵;Cf为瑞利阻尼矩阵,由质量矩阵和刚度矩阵按比例组合构造而成。
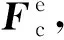
( 3 )
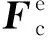
根据以上分析,建立2种结构的刚柔过渡接触网仿真模型,见图5。
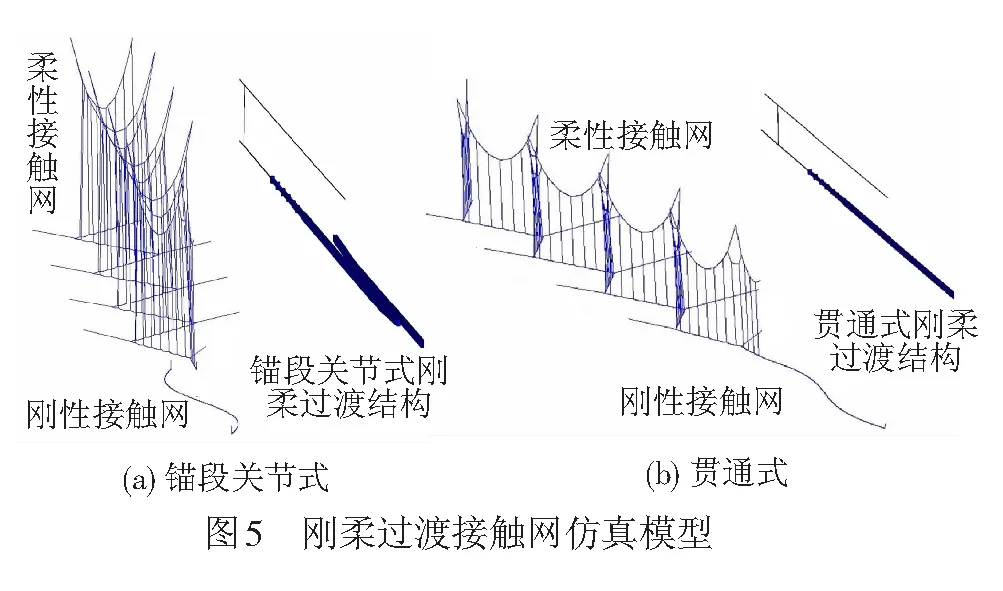
图5(a)利用锚段关节结构实现刚柔过渡,柔性接触网接触线首先连接刚柔过渡汇流排,然后连接汇流排终端,与刚性接触网的汇流排终端形成锚段关节结构。图5(b)利用刚柔过渡汇流排直接将柔性接触网与刚性接触网连接起来,在刚柔过渡汇流排后第2或第3个定位点约束所有自由度。
对2种刚柔过渡接触网仿真模型进行静平衡状态,得出接触网仅受自重和张力下的节点位移,见图6。图6(a)中在接触网里程250 m左右有2处接触线位移变大,为2个汇流排终端。图6(b)中在接触网里程250 m左右接触线位移较平稳过渡。2种刚柔过渡结构的刚性接触网和柔性接触网区段的接触线位移基本重合。柔性接触网接触线位移范围比刚性接触网大。
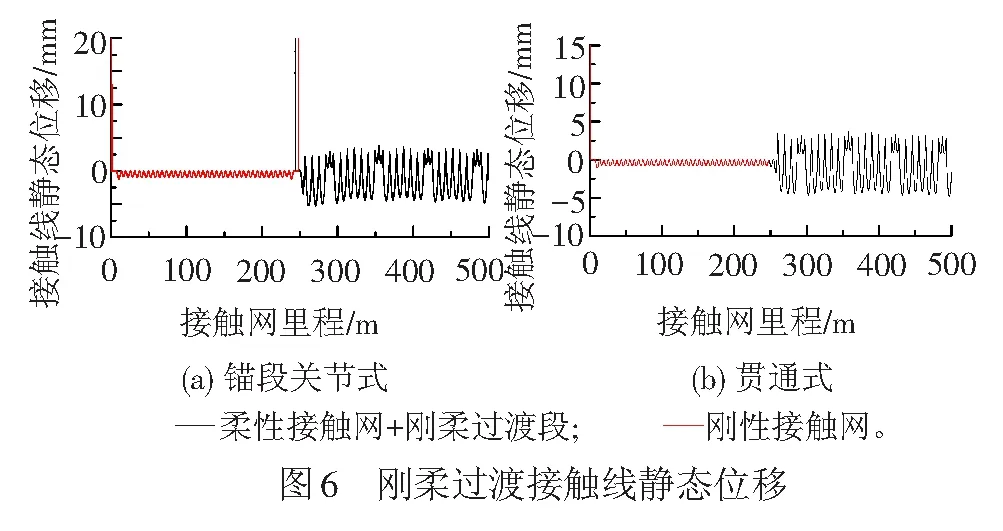
受电弓与接触网动力耦合的主要行为是滑动接触。一般解决接触问题的方法是利用罚函数。令接触线单元i-j与质量点m3的垂直方向渗透位移为Δξ,假设质量点m3在单元i-j上方位移Δξ为正值,此时为接触渗透状态,反之质量点m3在单元i-j下方位移Δξ为负值,见图7。
根据每个时间步Δξ的符号判断受电弓与接触线的接触状态,再根据接触刚度与Δξ的乘积作为分别作用于接触线和受电弓弓头质点的接触力,作为下一时间步接触网和受电弓的外部载荷重新计算节点位移,如此反复,即可计算弓网相互作用。接触力的大小为
( 4 )
联立受电弓动力方程式( 1 )、接触网动力方程式( 2 )、接触网单元接触力分配方程式( 3 )和接触力大小计算方程式( 4 ),组成统一的弓网动力仿真方程组。利用Newmark-β隐式积分算法,迭代求解弓网动力仿真组,得到弓网节点位移和接触力,进行弓网动力性能评估。
3 锚段关节式刚柔过渡仿真结果
标准TB/T 3271[16]中规定,交流系统小于200 km/h,接触力范围为0~300 N。接触力标准差的最大值不应超过0.3倍的平均接触力目标值。接触力标准差越小表示接触力的集中程度越高,弓网接触质量越好。
由于柔性接触网和刚性接触网的接触线静态位移不一样以及两者的刚度不一样,受电弓通过刚柔过渡结构的2个方向的动力响应不一样。故每种刚柔过渡结构分2个方向进行分析。
3.1 柔性接触网过渡到刚性接触网
受电弓以180 km/h速度等级从柔性接触网运行至刚性接触网,分析0~500 m区间的接触力。锚段关节处的双弓接触力出现了0值,双弓运行在柔性接触网的接触力波动均比刚性接触网大,锚段关节处的接触力在整个分析区间内的波动最大,出现最值。为受电弓能平稳通过刚柔过渡段,采用降低受电弓运行速度的方法,不同速度等级的弓网接触力见图8,当运行速度为100 km/h时,相对运行速度180 km/h弓网接触力波动小许多,且锚段关节处的接触力范围符合标准要求。

当受电弓从柔性接触网经锚段关节式过渡至刚性接触网时,受电弓的运行速度需要减速至100 km/h,才满足接触力标准要求。
将100 km/h速度等级下受电弓通过不同区段的接触力分别进行数理统计,见表5。双弓的刚性接触网的接触力标准差明显比柔性接触网的小。从接触力的数理统计特征值上看,柔性接触网的接触力波动较刚性大,刚柔过渡区段的接触力标准差最大,刚柔过渡区段是制约受电弓是否能顺利过渡的关键环节。
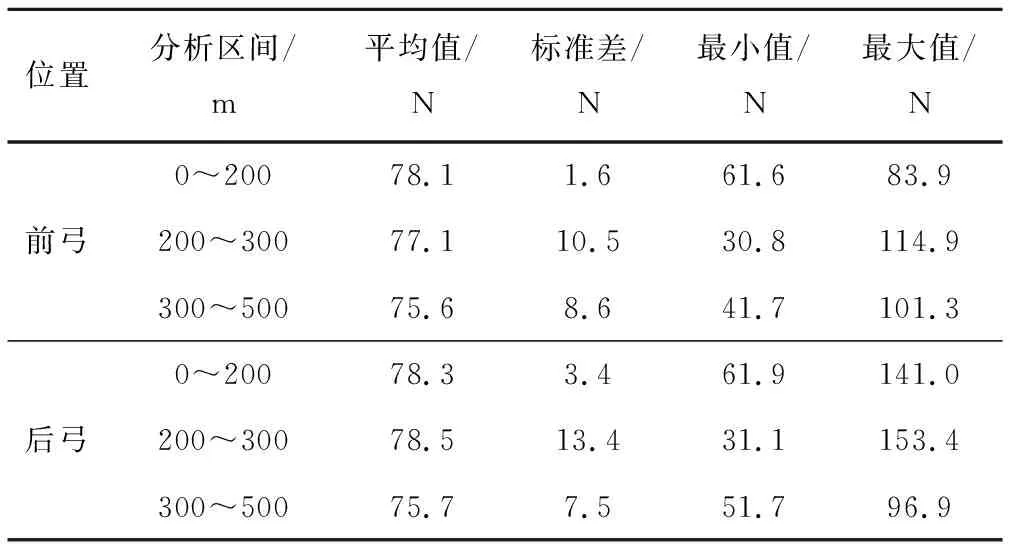
表5 100 km/h速度等级下柔性接触网经锚段关节过渡至刚性接触网接触力统计特征值
3.2 刚性接触网过渡到柔性接触网
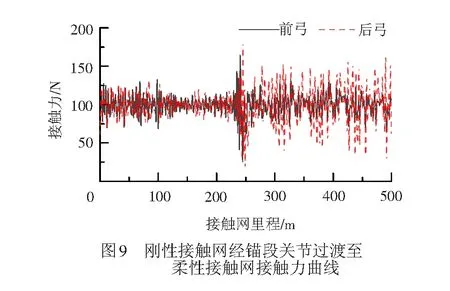
受电弓以180 km/h速度等级从刚性接触网过渡至柔性接触网,双弓接触力波形见图9,锚段关节处的接触力波动最大,最小值大于0,柔性接触网接触力波动比刚性接触网大。
分区段统计的接触力数据见表6,双弓接触力的统计值均符合标准要求。柔性接触网后弓的接触力比前弓的波动大,后弓的接触力标准差为前弓的2倍,说明柔性接触网后弓的弓网动力性能较差。刚性接触网双弓的接触力标准差、接触力最值比较接近,说明双弓对刚性接触网的影响较小,而对柔性接触网的影响较大。
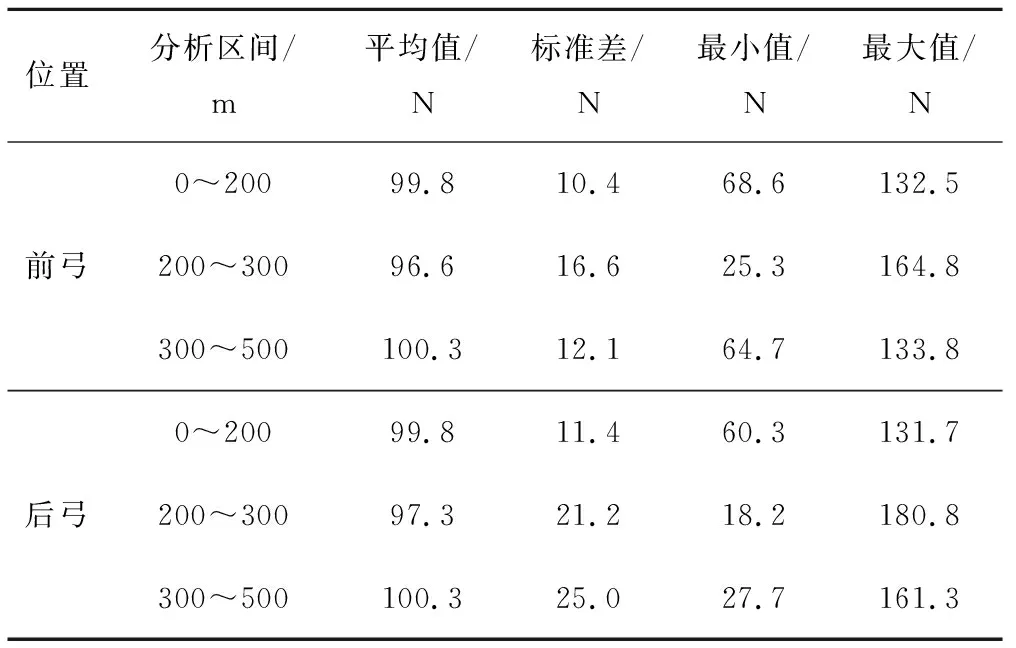
表6 180 km/h速度等级刚性接触网经锚段关节过渡至柔性接触网接触力统计特征值
4 贯通式刚柔过渡仿真结果
4.1 柔性接触网过渡到刚性接触网
图10为柔性接触网贯通过渡至刚性接触网不同速度等级双弓接触力曲线。受电弓以180 km/h速度等级匀速从柔性接触网经贯通式刚柔过渡至刚性接触网,双弓在刚柔过渡处的接触力波动较大,并出现0值,不满足标准要求。
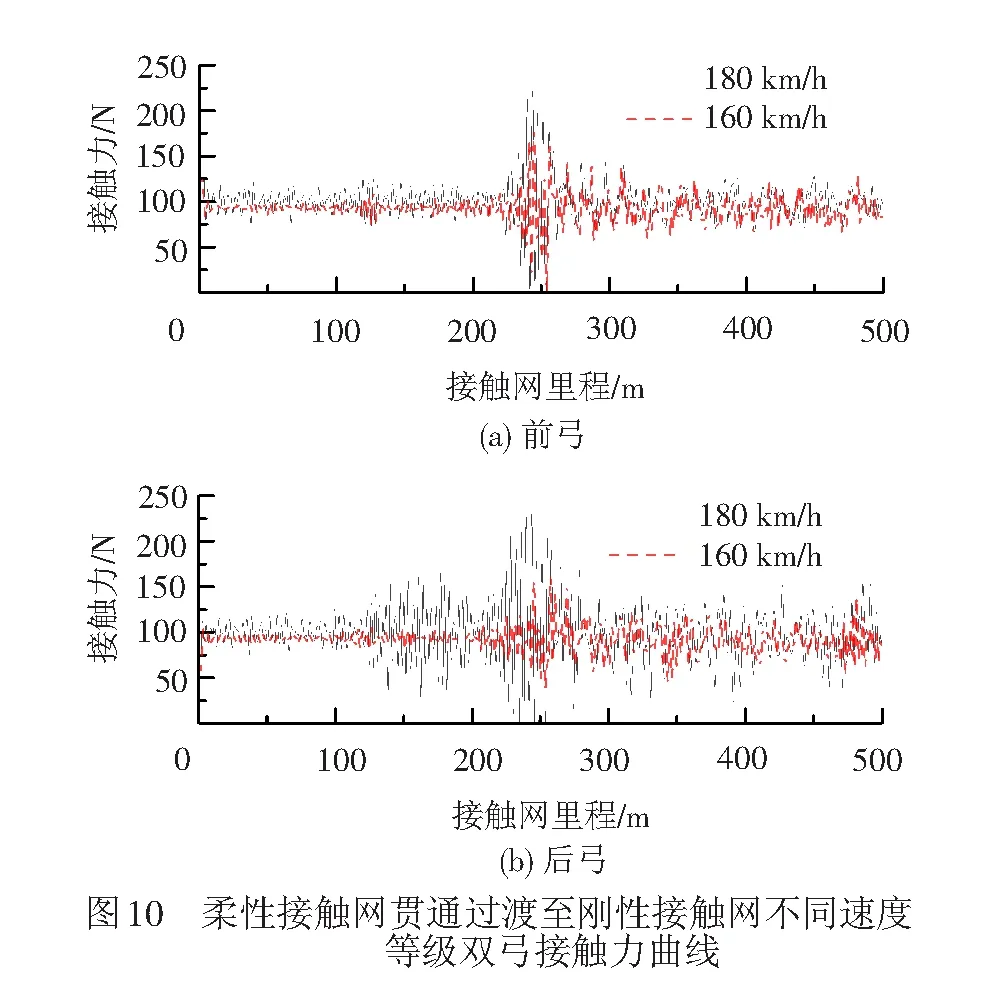
与锚段关节式刚柔过渡一样,降低受电弓运行速度至160 km/h,通过相同结构的接触网,对比180 km/h速度等级,接触力整体波动减小,尤其在刚柔过渡区段。
分区段统计160 km/h速度等级下受电弓从柔性接触网过渡至刚性接触网的接触力特征值,见表7,刚柔过渡区段的接触力标准差明显比刚性接触网、柔性接触网大。所有接触力统计指标均符合标准要求。
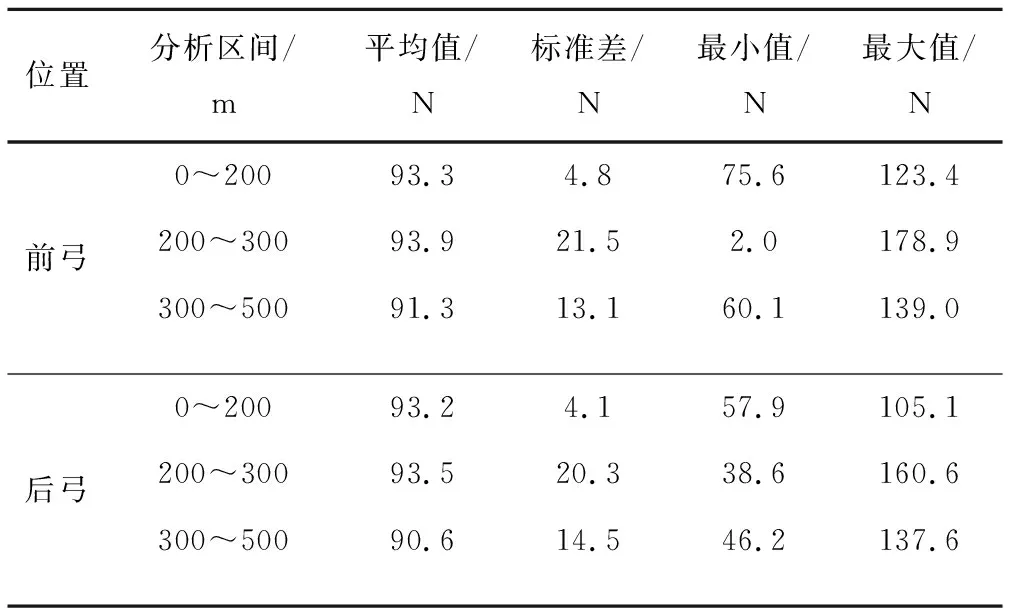
表7 160 km/h速度等级下柔性接触网贯通过渡至刚性接触网接触力统计特征
4.2 刚性接触网过渡到柔性接触网
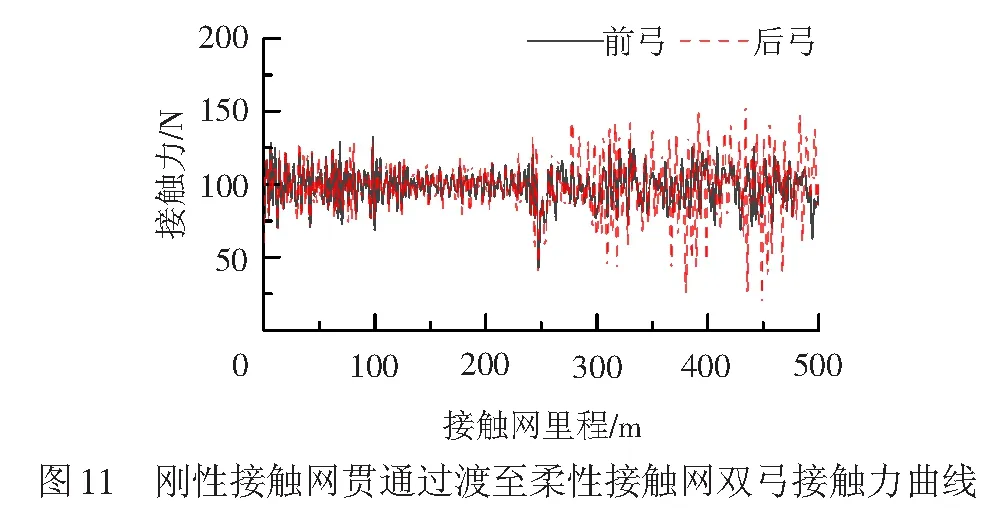
同样的接触网模型,受电弓以180 km/h速度等级从刚性接触网贯通过渡至柔性接触网,经弓网仿真,得到双弓的接触力曲线,见图11。相比图9,刚柔过渡处的接触力波动并不是最大的,柔性接触网的接触力波动最大,从接触网分析区段看,接触力范围均在标准范围内。
分区段统计受电弓从刚性接触网贯通过渡至柔性接触网的双弓接触力特征值,见表8。刚性接触网区段与刚柔过渡区段的接触力标准差相当,而柔性接触网的接触力标准差较大,后弓接触力标准差是前弓的2倍,与表6中柔性接触网双弓结果相似,说明后弓从刚性接触网过渡至柔性接触网受到前弓的影响,后弓的接触力波动较大。
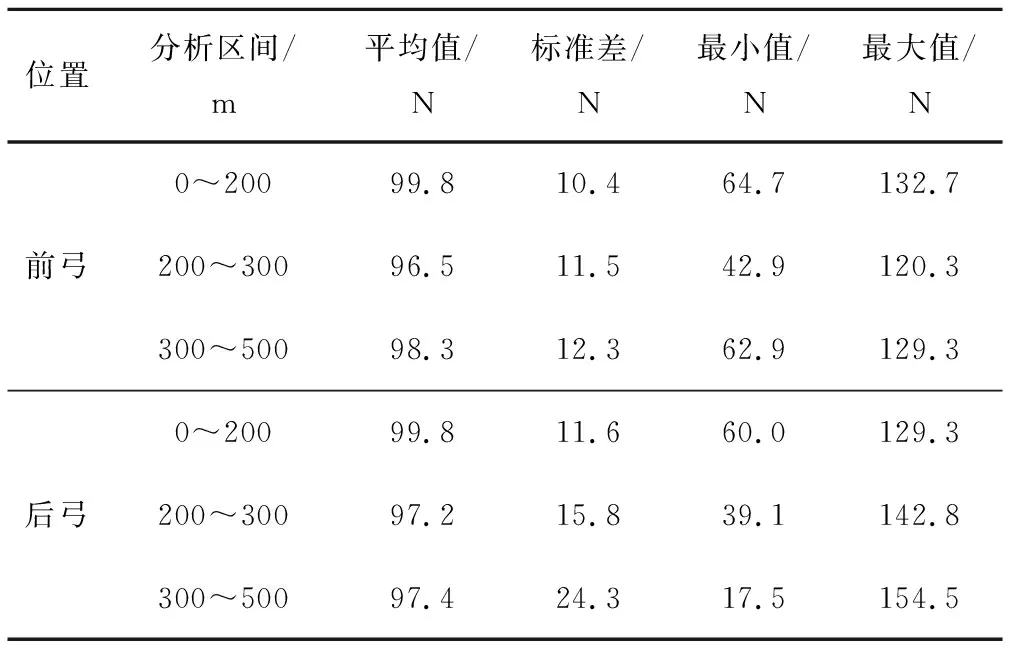
表8 180 km/h速度等级刚性接触网贯通过渡至柔性接触网接触力统计特征值
4.3 定位点增加弹性后柔性接触网过渡到刚性接触网
2种刚柔过渡结构从柔性接触网到刚性接触网均不满足180 km/h的速度要求,但贯通式刚柔过渡弓网动力性能较优。文献[17]研究表明定位点使用弹性线夹减小刚度能提高弓网接触质量,定位点刚度宜取7.6104N/m。结合图10中接触力在刚柔过渡处波动较大,研究减小该处定位点刚度对贯通式刚柔过渡的弓网动力性能的影响,见图12。
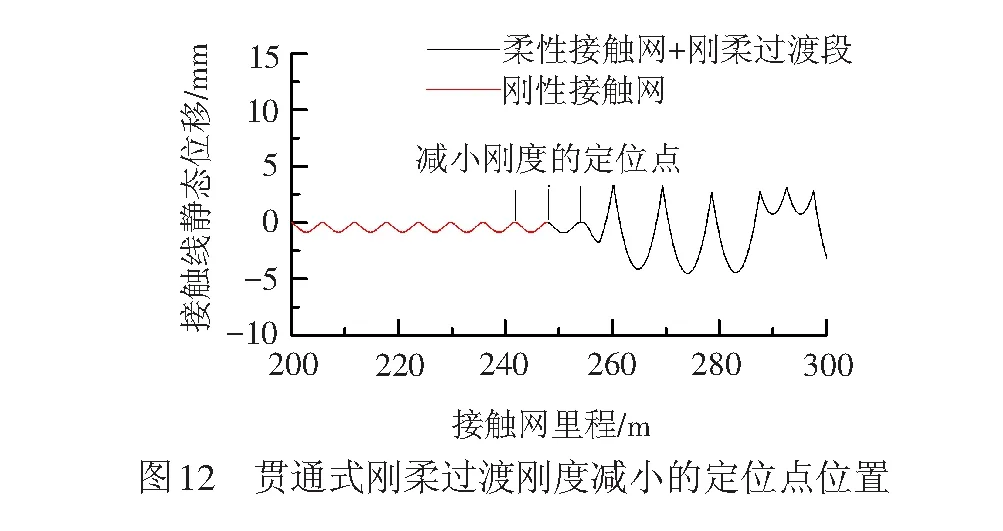
与图5(b)的贯通式刚柔过渡接触网模型相同,仅将图12中3个定位点刚度减小至7.6104N/m。DSA250受电弓以180 km/h速度等级从柔性接触网过渡至刚性接触网,得到双弓接触力曲线,见图13,双弓接触力范围均没超标。

表9中双弓各分析区段的接触力最值在标准范围,0.3倍平均接触力减标准差大于0,符合标准要求,说明定位点刚度减小能提高弓网接触质量,满足运行速度180 km/h。
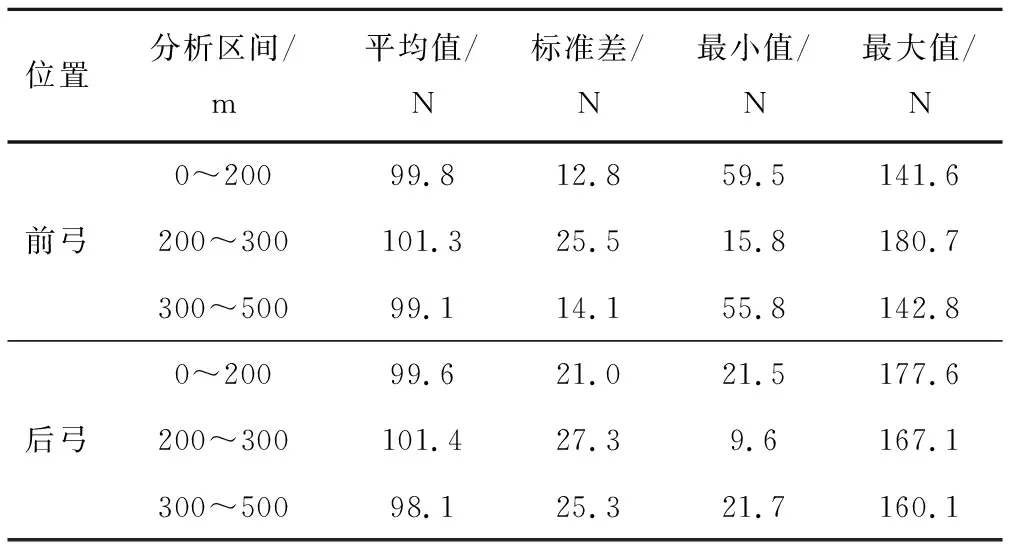
表9 180 km/h速度等级柔性接触网贯通过渡至弹性定位的刚性接触网接触力统计特征值
5 刚性接触网不平顺对刚柔过渡的影响
通过第4节研究得到了不考虑刚性接触网不平顺时的160 km/h刚柔过渡系统方案,宜采用贯通式刚柔过渡。以下研究在刚性接触网在施工过程中定位点安装误差带来的接触线高度不平顺对刚柔过渡系统方案的影响,以校验本方案的工程实施性。
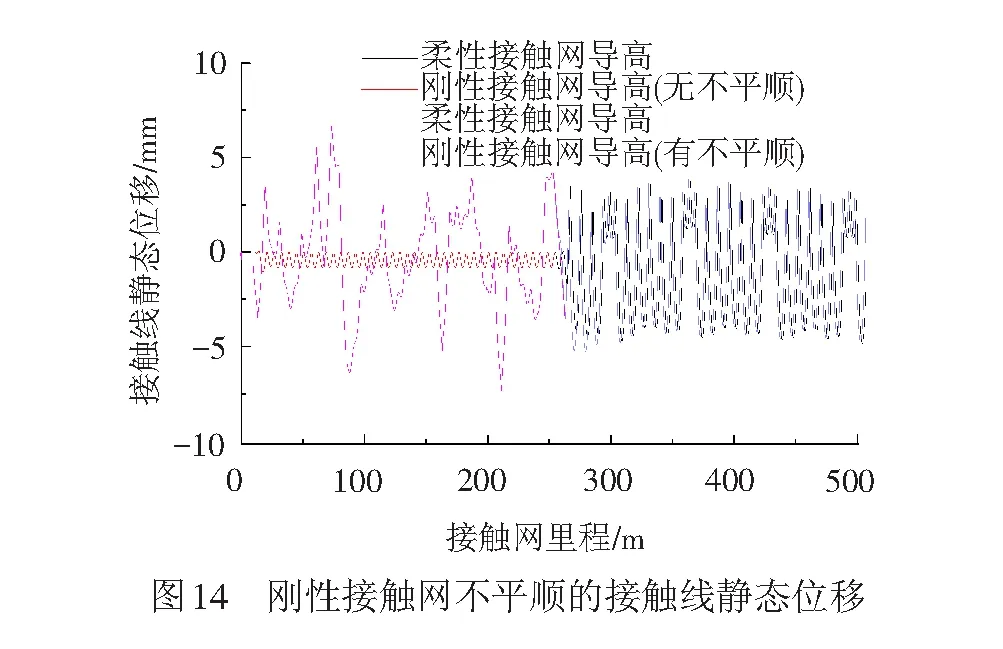
刚性接触网定位点安装误差控制在±10 mm范围内,本文假设安装误差服从正态分布规律,考虑正态分布规律中99.7%的数值落在3倍标准差范围内,选择均值为0 mm,标准差为3 mm的正态分布随机数来模拟实际的定位点安装误差(此时,99.7%的定位点安装误差在±9 mm范围内)。根据正态分布的随机数,建立刚性接触网的仿真模型,见图14。可以看出,当刚性接触网存在不平顺时,刚性接触网接触线静态位移的变化较大。
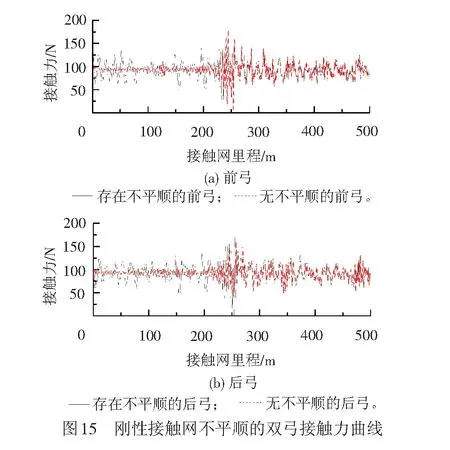
由于受电弓从柔性接触网过渡至刚性接触网的刚柔过渡区段接触力标准差比另一运行方向大,仅比较柔性接触网过渡至刚性接触网的接触力。当受电弓以160 km/h速度从柔性接触网过渡至存在不平顺的刚性接触网,经弓网仿真,得到弓网接触力波形见图15。刚性接触网存在不平顺对接触力的影响显著,此时,柔性接触网与刚性接触网的接触力波动幅值接近。
统计刚性接触网不平顺的接触力数理统计值,见表10。表10中发现柔性接触网和刚性接触网的接触力标准差接近。双弓各分析区段的接触力最值在标准范围,0.3倍平均接触力减标准差大于0,符合标准要求,说明考虑刚性接触网不平顺的刚柔过渡系统方案仍满足160 km/h的运行速度要求。
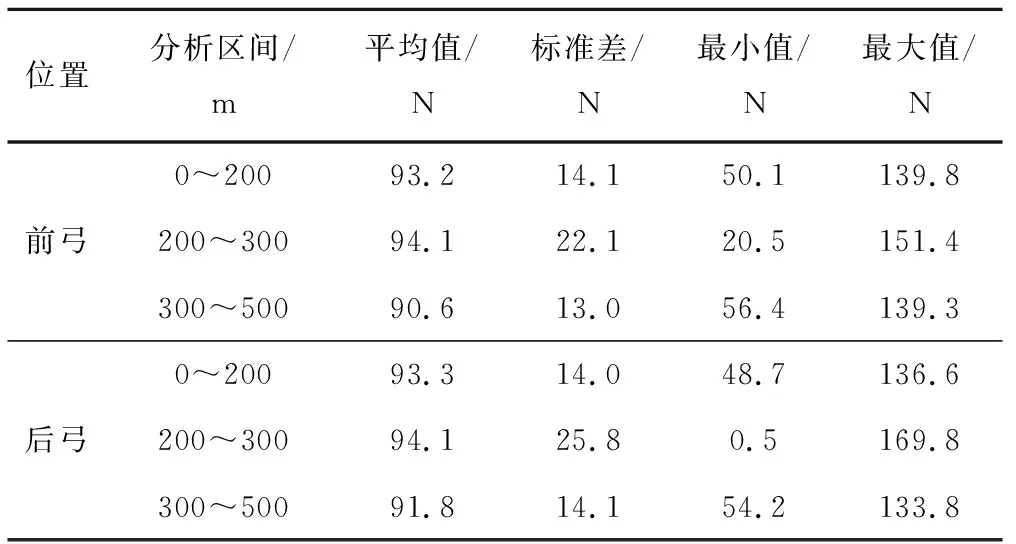
表10 刚性接触网不平顺的接触力统计特征值
对比表7和表10后弓的接触力统计值,发现刚性接触网存在不平顺的后弓接触力标准差变大,最小接触力接近0,不平顺对后弓接触力的影响显著。若双弓通过刚柔过渡结构,应尽量减小刚柔过渡段的刚性接触网不平顺。
6 结论
(1) 建立锚段关节式和贯通式2种结构的刚柔过渡接触网仿真模型,刚性接触网采用跨距为6 m,定位点刚性悬挂,柔性接触网采用德国Re250型。受电弓使用DSA250型,双弓间距200 m。比较2种刚柔过渡的弓网动力性能,得出了贯通式刚柔过渡能满足速度160 km/h的要求。
(2) 比较不同工况下双弓接触力,得出刚柔过渡区段的接触力标准差是最大的,说明刚柔过渡区段是制约受电弓是否能顺利过渡的关键环节。
(3) 比较不同工况下双弓接触力,发现后弓各区段的接触力标准差比前弓大,说明后弓是制约刚柔过渡动力响应的主要参数。
(4) 刚柔过渡处定位点的刚度减小能在一定程度上提高弓网动力性能,将运行速度提升至180 km/h。
(5) 考虑了刚性接触网存在定位点均值为0 mm、标准差为3 mm的正态分布安装误差工况下的不平顺,当受电弓以160 km/h速度等级通过刚柔过渡系统方案时,弓网动态性能仍能满足标准要求,校验了本方案的工程实施性。
