应用能量观点解决动力学问题
2018-09-28湖南省汨罗市第一中学周辉林
■湖南省汨罗市第一中学 周辉林
利用动能定理、机械能守恒定律、能量的转化和守恒定律来分析动力学问题,称之为应用能量的观点分析求解动力学问题。若题目没有涉及加速度和时间,则无论是恒力做功还是变力做功,不管是直线运动还是曲线运动,动能定理均适用。当只存在动能、势能的相互转化时,则应用机械能守恒定律。当存在除机械能以外的其他能量时,则应用能量的转化和守恒定律。
一、动能定理的应用
例1我国将于2022年举办冬奥会,跳台滑雪是其中最具观赏性的项目之一。如图1所示,质量m=60kg的运动员从长直助滑道AB的A处由静止开始以加速度a=3.6m/s2匀加速滑下,到达助滑道末端B时的速度vB=24m/s,A、B两点间的竖直高度差H=48m。为了改变运动员的运动方向,在助滑道与起跳台之间用一段弯曲滑道衔接,其中最低点C处附近是一段以O为圆心的圆弧。助滑道末端B与滑道最低点C的高度差h=5m,运动员在B、C两点间运动时,阻力做功W=-1530J,取g=10m/s2。

图1
(1)求运动员在滑道AB上下滑时受到阻力f的大小。
(2)若运动员能够承受的最大压力为其自身重力的6倍,则C点所在圆弧的半径R至少应为多大?
解析:(1)运动员在滑道AB上做初速度为零的匀加速运动,设滑道AB的长度为x,则,解得x=80m。由牛顿第二定律得,解得
(2)设运动员到达C点时的速度为vC,则运动员在从B点运动到C点的过程中,由动能定理得解得vC=25m/s。设运动员在C点所受的支持力为N,由牛顿第二定律得N-mg=由题意和牛顿第三定律得N=6mg。联立以上各式解得R=12.5m。
思维方法:利用动能定理时,需要先确定研究对象,做好受力分析和过程分析,再判断哪些力做功、哪些力不做功、哪些力做正功、哪些力做负功,然后确定总功及初、末状态物体的动能,最后列动能定理方程求解。
二、机械能守恒定律的应用

图2
例2如图2所示,由四分之一圆弧AB和二分之一圆弧BC组成的光滑轨道固定在竖直平面内,两者在最低点B平滑连接。AB弧的半径为R,BC弧的半径为。一小球从A点正上方与A点相距处由静止开始自由下落,经A点沿圆弧轨道运动。
(1)求小球在B、A两点的动能之比。
(2)通过计算判断小球能否沿轨道运动到C点。
解析:(1)设小球的质量为m,小球在A点的动能为EkA,由机械能守恒定律得EkA=mg·。设小球在B点的动能为E,同理kB得
(2)若小球能沿轨道运动到C点,则小球在C点所受轨道的支持力N应满足N≥0。设小球在C点的速度大小为vC,由牛顿第二定律和向心力公式得解得在小球从开始下落至到达C点的全过程中,由机械能守恒定律得mg·解得因此小球恰好可以沿轨道运动到C点。
思维方法:利用机械能守恒定律时,需要先确定研究对象,做好受力分析和过程分析,再判断是否符合机械能守恒的适用条件,然后选取初、末状态并确定初、末状态的机械能,最后列机械能守恒定律方程求解。
三、能量的转化和守恒定律的应用

图3
例3如图3所示,固定斜面的倾角θ=30°,物体A与斜面间的动摩擦因数轻弹簧下端固定在斜面底端,弹簧处于原长时其上端位于C点。用一根不可伸长的轻绳跨过轻质光滑的定滑轮连接物体A和B,滑轮右侧的轻绳与斜面平行,物体A的质量为2m,物体B的质量为m,初始时物体A到C点的距离为L。现给物体A、B一初速度使物体A开始沿斜面向下运动,物体B竖直向上运动,物体A将弹簧压缩到最短后又恰好能弹回到C点。已知重力加速度为g,不计空气阻力,整个过程中轻绳始终处于伸直状态,求:
(1)物体A向下运动刚到C点时的速度。
(2)弹簧的最大压缩量。
(3)弹簧的最大弹性势能。
解析:(1)物体A与斜面间的滑动摩擦力f=2μmgcosθ,物体A在从初始位置向下运动到C点的过程中,根据能量的转化和守恒定律得解得
(2)在物体A刚接触弹簧到将弹簧压缩到最短后又恰好能弹回到C点的整个过程中,对由物体A、B组成的系统应用动能定理得解得
(3)在弹簧被压缩到最短到恰好能弹回到C点的过程中,对由物体A、B组成的系统应用能量的转化和守恒定律得Ep+mgx=2mgxsinθ+fx,解得
思维方法:利用能量的转化和守恒定律时,需要先确定研究对象,做好受力分析和过程分析,再明确有哪些力做功,做功的结果是导致了何种形式的能量相互转化,然后建立ΔE增=ΔE减的关系求解或讨论。


图4
1.如图4所示,质量为m的小球用长为L的细线悬挂而静止在竖直位置。现用水平拉力F将小球缓慢地拉到细线与竖直方向成θ角的位置。在此过程中,拉力F做的功为( )。
A.FLcosθ
B.FLsinθ
C.FL(1-cosθ)
D.mgL(1-cosθ)
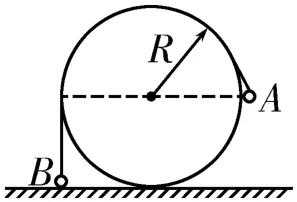
图5
2.如图5所示,可视为质点的小球A、B用不可伸长的细软轻线连接,跨过固定在地面上、半径为R的光滑圆柱,A球的质量为B球的两倍。当B球位于地面时,A球恰与圆柱轴心等高。将A球由静止释放,B球上升的最大高度是( )。


图6
3.如图6所示,质量为M、长度为L的小车静止在光滑水平面上。质量为m的小物块(可视为质点)放在小车的最左端。现用一水平恒力F作用在小物块上,使小物块从静止开始做匀加速直线运动,小物块和小车间的摩擦力为f,小物块滑到小车的最右端时,小车运动的距离为s。在这个过程中,以下结论正确的是( )。
A.小物块到达小车最右端时具有的动能为F(L+s)
B.小物块到达小车最右端时,小车具有的动能为fs
C.小物块克服摩擦力所做的功为f(L+s)
D.小物块和小车增加的机械能为fs
参考答案:1.D 2.C 3.BC
