全国名校等差数列拔高卷(B卷)

2018-09-28山东省枣庄市第二中学王中华

中学生数理化(高中版.高二数学) 2018年9期

关键词：正整数公差销售量

■山东省枣庄市第二中学王中华

编者的话：强化对核心考点的演练、注重对经典题型的归纳,是学好数学的秘诀,基于此,本刊编辑部特开设此栏目,希望同学们能认真练习。

一、选择题

1.x+3与y-3的等差中项为20,则x+y等于( )。

A.60 B.40 C.20 D.不确定

2.等差数列{an}中,若a8-a3=40,则a2025-a2020=( )。

A.40 B.30 C.25 D.20

3.已知等差数列{an}满足a2=0,a6+a8=-10,则a2019=( )。

A.2 017 B.2 015

C.-2 017 D.-2 015

4已知{an}是等差数列,且a1+a4+a7=45,a2+a5+a8=39,则a3+a6+a9的值是( )。

A.24 B.27 C.30 D.33

5.已知等差数列{an}中,其前n项和为Sn,若a3+a4+a5=42,则S7=( )。

A.98 B.49 C.14 D.147

6.设Sn为等差数列{an}的前n项和,若3S3=S2+S4,a1=2,则a5=( )。

A.-12 B.-10 C.10 D.12

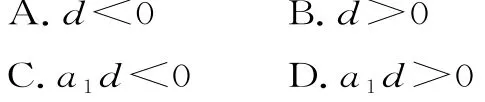
8.若等差数列{an}满足a5=11,a12=-3,数列{an}的前n项和Sn的最大值为M,则lgM=( )。

A.1 B.2 C.10 D.100

9.《九章算术》之后,人们进一步用等差数列求和公式来解决更多的问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第二天开始,每天比前一天多织相同量的布),第一天织5尺布,现在一月(按30天计),共织390尺布”,则从第二天起每天比前一天多织( )尺布。

10.设等差数列{an}的前n项和为Sn,若S4≥10,S5≤15,则a4的最大值为( )。

A.2 B.3 C.4 D.5

11.设等差数列{an}的前n项和为Sn,若a1=-11,a4+a6=-6,则当Sn取最小值时,n等于( )。

A.6 B.7 C.8 D.9

12.设{an}是公差为-2的等差数列,若a1+a4+a7+…+a97=50,则a3+a6+a9+…+a99等于( )。

A.82 B.-82 C.132 D.-132

13.已知数列{an}是首项为1,公差为d(d∈N*)的等差数列,若81是该数列中的其中一项,则公差d不可能是( )。

A.2 B.3 C.4 D.5

14.《九章算术》是我国古代一部重要的数学著作,书中有如下问题:“今有良马与驽马发长安,至齐。齐去长安三千里,良马初日行一百九十三里,日增一十三里;驽马初日行九十七里,日减半里。良马先至齐,复还迎驽马,问几日相逢。”其意为:“现在有良马和驽马同时从长安出发到齐去。已知长安到齐的距离是3000里,良马第一天行193里,之后每天比前一天多行13里;驽马第一天行97里,之后每天比前一天少行0.5里。良马到齐后,返回去迎驽马,多少天后两马相遇?”利用我们所学的知识,可知离开长安后的第( )天,两马相逢。

A.15 B.16 C.17 D.18

15.已知等差数列{an}的公差为正数,前n项和为Sn,且a3·a7=-12,a4+a6=-4,则S20为( )。

A.180 B.-180 C.90 D.-90

16.已知等差数列{an}的前n项和为Sn,若S9=18,Sn=240,an-4=30,则n的值为( )。

A.14 B.15 C.16 D.17

17.在正整数100至500之间能被11整除的数的个数为( )。

A.34 B.35 C.36 D.37

18.等差数列{an}中,已知a1=-6,an=0,公差d∈N*,则n(n≥3)的最大值为( )。

A.5 B.6 C.7 D.8

19.已知数列{an}满足a1=15,且3an+1=3an-2,若ak·ak+1＜0,则正整数k=( )。

A.24 B.23 C.22 D.21

20.若数列{an}是等差数列,首项a1＞0,a2003+a2004＞0,a2003·a2004＜0,则使前n项和Sn＞0成立的最大自然数n是( )。

A.4005 B.4006

C.4007 D.4008

21.设等差数列{an}的前n项和为Sn,且S5=13,S15=63,则S20=( )。

A.90 B.100 C.110 D.120

24.(2017届湖南省长沙市一中高三月考)“珠算之父”程大位是我国明代的伟大数学家,他的应用数学巨著《算法统宗》的问世,标志着我国的算法由筹算到珠算转变的完成。程大位在《算法统宗》中常以诗歌的形式呈现数学问题,其中有一道“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上梢四节贮三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明。”([注释]三升九:3.9升。次第盛:盛米容积依次相差同一数量。)用你所学的数学知识求得中间两节的容积为( )。

A.1.9升 B.2.1升

C.2.2升 D.2.3升

A.16 B.14 C.12 D.10

28.等差数列{an}有两项am,ak(m≠k),满足a=,a=,则该数列前mk项mk之和为( )。

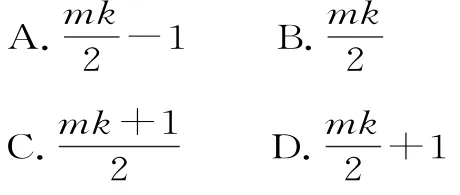
29.等差数列{an}的公差d＜0,且=014,若数列{an}的前n项和Sn最大,Sm=0,则m-n的值( )。

32.把正整数按“S”型排成了如图1所示的三角形数表,第n行有n个数,对于第n行按从左往右的顺序依次标记第1列,第2列,…,第m列(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2015在( )。

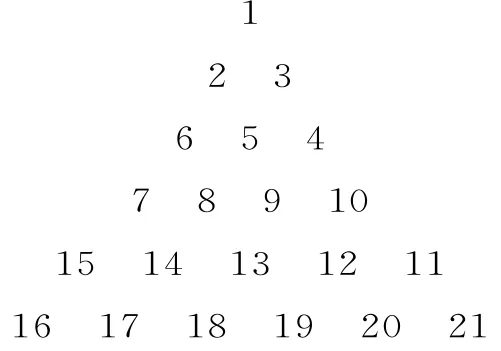
图1

A.第63行第2列

B.第62行第12列

C.第64行第30列

D.第64行第60列

33.若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,则这个数列的项数为( )。

A.13 B.12 C.11 D.10

34.在等差数列{an}中,对任意n∈N*,都有an＞an+1,且a2,a8是方程x2-12x+m=0的两根,且前15项的和S15=m,则数列{an}的公差是( )。

A.-2或-3 B.2或3

C.-2 D.-3

35.已知函数f(x)在(-1,+∞)上单调,且函数y=f(x-2)的图像关于x=1对称,若数列{an}是公差不为0的等差数列,且f(a100)=f(a101),则{an}的前200项的和为( )。

A.-200 B.-100

C.0 D.-50

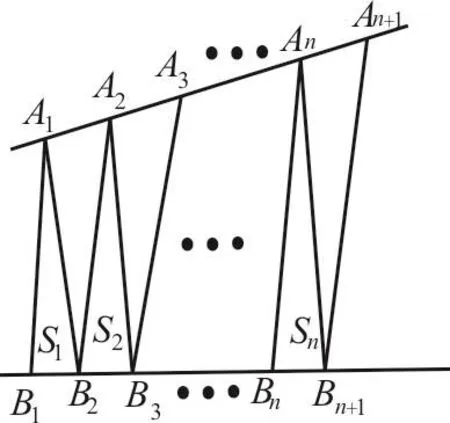
图2

37.如图2所示,点列{An},{Bn}分别在某锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N*,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N*,P≠Q表示点P与点Q不重合。若dn=|AnBn|,Sn为△AnBnBn+1的面积,则( )。

二、填空题

38.(2018年高考北京理数第9题)设{an}是等差数列,且a1=3,a2+a5=36,则{an}的通项公式为。

39.(2018年高考北京文数第15题改编)设{an}是等差数列,且a1=ln2,a2+a3=5ln2,则数列{an}的通项公式为。

40.(2018年福建省“四地六校”联考)在数列{an}中,a1=1,an+2+(-1)nan=1,记Sn是数列{an}的前n项和,则S200=。

41.(2017年高考课标Ⅱ卷理数第15题)等差数列{an}的前n项和为Sn,a3=3,S4=10,则=。

42.已知数列{an},{bn}都是公差为1的等差数列,其首项分别为a1,b1,且a1+b1=5,a1＞b1,a1、b1∈N*,n∈N*,则数列{abn}的前10项的和等于。

43.在数列{an}中,a1=1,an+1=(n∈N*),则是这个数列的第项。

44.一个卷筒纸,其内圆直径为3cm,外圆直径为15cm,一共卷了72层,若把各层都视为同心圆,π的值取3.14,则这个卷筒纸的长度大约为m(精确到个位)。

45.我国古代数学名著《张丘建算经》有“分钱问题”,如下:“今有人与钱,初一人与三钱,次一人与四钱,次一人与五钱,以次与之,转多一钱,与讫,还数聚与均分之,人得一百钱,问人几何。”则分钱问题中的人数为。

46.中位数为1010的一组数构成等差数列,其末项为2015,则该数列的首项为。

47.在等差数列｛an｝中,a1＞0,a10·a11＜0,若此数列的前10项和S10=36,前18项的和S18=12,则数列｛ an｝的前18项和T18的值是。

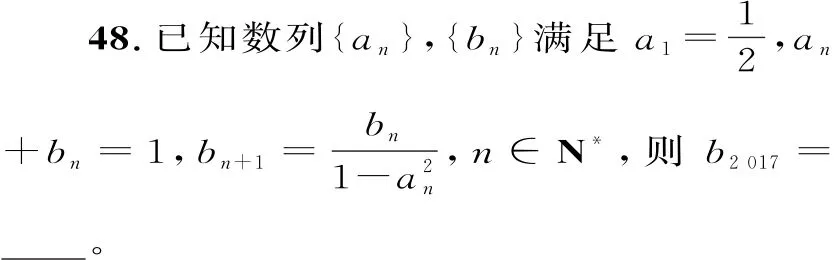
49.(湖北省黄冈市2017届高三上学期期末考试数学(文)试题第16题)“中国剩余定理”又称“孙子定理”。1852年英国来华传教士伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲。1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”。“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2017这2016个数中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列{an},则此数列的项数为。

50.已知数列{an}的前n项和Sn满足an+3Sn·Sn-1=0,n≥2,n∈N*,且a1=,则nan的最小值为。